
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Минимизация логических функцийСодержание книги
Поиск на нашем сайте Задача минимизации логической функции заключается в том, чтобы найти наиболее компактное ее представление в виде нормальной формы минимальной сложности – минимальной дизъюнктивной нормальной формы (МДНФ) или минимальной конъюнктивной нормальной формы (МКНФ). Минимальная нормальная форма – это нормальная форма, содержащая минимальное количество переменных, использованных с отрицанием или без. Минимальная дизъюнктивная нормальная форма – это дизъюнкция минимального числа конъюнкций переменных, взятых с отрицанием или без. Минимальная конъюнктивная нормальная форма – это конъюнкция минимального числа дизъюнкций переменных, взятых с отрицанием или без. Метод эквивалентных логических преобразований Получение МДНФ (МКНФ) через упрощение СДНФ (СКНФ) по правилам преобразования.
Диаграмма Вейча (карта Карно) Графический способ минимизации логических функций. Работает на основе операций склеивания и поглощения. Представляет собой особым образом переупорядоченную таблицу истинности. Операция склеивания осуществляется между двумя совершенными конъюнктами (дизъюнктами), у которых совпадают все литералы, кроме одного. По правилам склеивания совпадающие литералы выносятся за скобки, а оставшиеся подвергнуть склейке.
В диаграмме Вейча ячейки таблицы истинности сгруппированы таким образом, что переход из одной ячейки в другую по вертикали или горизонтали связан с изменением значения только одной переменной. В результате этого наборы, между которыми возможно склеивание, получаются сгруппированными вместе и их легко заметить. Метод Вейча подходит для минимизации функций до 7 переменных. При большем количестве теряются достоинства метода. Интервал логической функции от · Значение функции на этом множестве постоянно; · Мощность (величина, размер интервала) этого множества равна · · Если Типы интервалов
Интервал размера 1 Вырожденный случай. Упрощения не происходит. Интервал может встречаться на любых диаграммах. Интервал размера 2 Упрощается одна переменная. Интервалы могут встречаться на любых диаграммах. Интервал размера 4 Упрощается 2 переменных. Некоторые интервалы встречаются, начиная с диаграммы Вейча для функции от 3 переменных. Интервалы размером 8 Упрощается 3 переменных. Некоторые интервалы встречаются, начиная с диаграммы Вейча для функции от 4 переменных. Алгоритм минимизации 1. Нарисовать исходную таблицу диаграммы и сделать ее разметку в зависимости от количества переменных функции. 2. Заполнить таблицу значениями функции с учетом цели минимизации (удобно выписывать только 1 для МДНФ и только 0 для МКНФ). 3. Выделить контурами интервалы из единиц (МДНФ) или нулей (МКНФ), соблюдая следующие правила: a. Необходимо стараться выделить максимально большие интервалы; b. Каждый новый интервал должен содержать хотя бы одно значение, принадлежащее только ему; c. Необходимо выделить минимально возможное количество интервалов. 4. Выписать формулу МДНФ (МКНФ), для чего: a. Для каждого интервала выписать конъюнкт (дизъюнкт), в который будут входить только те переменные или их отрицания, которые сохраняют свое значение на интервале. Остальные переменные упростятся. b. Соединить выписанные конъюнкты (дизъюнкты) через дизъюнкцию (конъюнкцию).
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-08-19; просмотров: 328; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

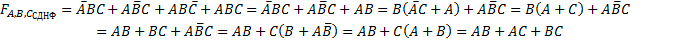
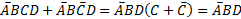
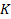 переменных – это такое множество наборов значений переменных, что:
переменных – это такое множество наборов значений переменных, что: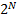 ,
,  ;
;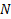 является количеством переменных, которые упрощаются на этом множестве, а оставшихся (
является количеством переменных, которые упрощаются на этом множестве, а оставшихся (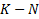 ) переменных достаточно для описания логической функции на данном множестве;
) переменных достаточно для описания логической функции на данном множестве;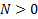 , то каждый следующий набор отличается от предыдущего значением только одной переменной.
, то каждый следующий набор отличается от предыдущего значением только одной переменной.


