
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ограничения точности для целых чиселСодержание книги
Поиск на нашем сайте
· Целые между 0 и 2047 представляются точно · Целые между 2048 и 4095 округляются вниз до кратного 2 (четному числу) · Целые между 4096 и 8191 округляются вниз до кратного 4 · Целые между 8192 и 16383 округляются вниз до кратного 8 · Целые между 16384 и 32767 округляются вниз до кратного 16 · Целые между 32768 и 65535 округляются вниз до кратного 32 Почему это происходит? Пусть дано число 500310=10011100010112=011001001110001011. Последние две цифры мантиссы оказались за пределами разрядной сетки. При обратном переводе в десятичную систему получим число 5000 – ближайшее округленное до кратного числу 4. Формат числа половинной точности
Смещение (или сдвиг) порядка: Формат числа одинарной точности
Под порядок выделено 8 бит, поэтому смещение: Формат двойной точности
Под порядок выделено 11 бит, поэтому смещение: Алгоритм получения числа с плавающей точкой 1. Перевести число из K-ичной системы счисления в двоичную (прямой код);
2. Представить двоичной число в нормализованной форме:
3. Рассчитать смещенный порядок числа:
4. Разместить знак, порядок и мантиссу в соответствующие разряды сетки;
5. Разбить полученное число на тетрады и записать полученные двоичные разряды в виде числа в 16-ичной системе.
Алгоритм восстановления десятичного числа 1. Расписать по знакам исходное 16-ричное число на двоичные разряды;
2. По первому биту определить знак числа;
3. Вычислить истинный порядок: из смещенного порядка вычесть сдвиг порядка;
4. Записать знак, подразумеваемую единицу, в дробную часть выписать мантиссу, умножить полученное число на
5. Перевести полученное число в десятичную систему счисления. Характеристики некоторых форматов стандарта
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-08-19; просмотров: 178; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.19.210 (0.008 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 – число, которое необходимо прибавить к истинному порядку исходного числа. Оно записывается в биты поля Порядок. Для формата половинной точности под порядок выделяется 5 бит разрядной сетки, т.е. максимальное смещенное значение порядка – 31.
– число, которое необходимо прибавить к истинному порядку исходного числа. Оно записывается в биты поля Порядок. Для формата половинной точности под порядок выделяется 5 бит разрядной сетки, т.е. максимальное смещенное значение порядка – 31. .
.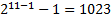 .
.
 ;
;
 , где
, где 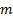 – смещение, зависящее от формата хранения;
– смещение, зависящее от формата хранения;
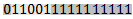




 , упростить полученное выражение;
, упростить полученное выражение;



