
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Совершенные конъюнктивная и дизъюнктивная нормальные формыСодержание книги
Поиск на нашем сайте
Конъюнкт – конъюнкция некоторых переменных или их отрицаний. Дизъюнкт – дизъюнкция некоторых переменных или их отрицаний. Если конъюнкт (дизъюнкт) состоит из всех переменных функции или их отрицаний, где каждая переменная участвует лишь единожды, то такой конъюнкт (дизъюнкт) называется совершенным. Минтерм (конституента единицы) – это логическая функция, принимающая значение истина только на одном наборе значений своих аргументов. Формальная запись минтерма – это конъюнкция всех аргументов функции, взятых с отрицанием или без него. Среди множества функций от Макстерм (конституента нуля) – это логическая функция, принимающая значение ложь только на одном наборе значений своих аргументов. Формальная запись макстерама – это дизъюнкция всех аргументов функции, взятых с отрицанием или без него. Среди множества функций от Дизъюнктивная нормальная форма (ДНФ) – дизъюнкция конечного числа конъюнктов. Совершенная ДНФ (СДНФ) – дизъюнкция совершенных конъюнктов (т.е. минтермов). Любая логическая функция, не являющаяся логическим нулем, имеет только одну СДНФ. Конъюнктивная нормальная форма (КНФ) – конъюнкция конечного числа дизъюнктов. Совершенная КНФ (СКНФ) – конъюнкция совершенных дизъюнктов (т.е. макстермов). Любая логическая функция, не являющаяся логической единицей, имеет только одну СКНФ. Выполнимая логическая функция - логическая функция, не являющаяся константой нуля или константой единицы. Представления выполнимой логической функции в виде СКНФ или СДНФ равнозначны, но иногда требуют разного количества операций.
Построение СДНФ по таблице истинности Выписать совершенные конъюнкции и связать их через дизъюнкцию.
Моделирование схемы СДНФ Схемотехническое представление Построение СКНФ по таблице истинности Выписать совершенные дизъюнкции и связать их через конъюнкцию.
Моделирование схемы СКНФ Схемотехническое представление
Логические законы и правила · Коммутативный
·
· Дистрибутивный
·
· Закон идемпотентности
·
· Правило склеивания
· Правило свертки
· Правило поглощения
· Законы де Моргана
· Правило раскрытия импликации
· Правила раскрытия эквивалентности
· Правило раскрытия строгой дизъюнкции
Лекция №5
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-08-19; просмотров: 176; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.124.119 (0.007 с.) |

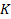 переменных есть
переменных есть 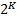 минтермов. Минтерм – это совершенный конъюнкт.
минтермов. Минтерм – это совершенный конъюнкт.
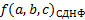 изображено ниже.
изображено ниже.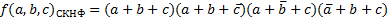
 изображено ниже.
изображено ниже.

 ,
,
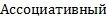
 ,
,
 ,
,
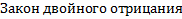

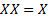 ,
,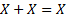 ,
, ,
, 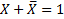
 ,
, ,
, ,
,
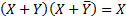 ,
,
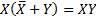 ,
,
 ,
,
 ,
,
 ,
,

 ,
,




