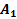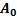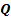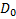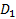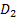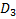Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диаграмма Вейча для функции от 2 переменныхСодержание книги
Поиск на нашем сайте
МДНФ:
МКНФ:
Диаграмма Вейча для функции от 3 переменных МДНФ:
МКНФ:
Диаграмма Вейча для функции от 4 переменных МДНФ:
МКНФ:
Наборы значений функции для МКНФ по отношению к МДНФ инвертируются.
Диаграмма Вейча для функции от 5 переменных МДНФ:
МКНФ:
Минимизация частично определенных логических функций В некоторых задачах нам известно, что определенные входные комбинации никогда не возникнут. В таком случае неопределенные значения интерпретируются так, как удобно.
Приведение минимизированной функции к заданному логическому базису На примере (МДНФ к базису ИЛИ-НЕ)
(МДНФ к базису И-НЕ)
(МКНФ к базису ИЛИ-НЕ)
(МКНФ к базису И-НЕ)
Лекция №6 Дешифраторы Дешифратор – комбинационная схема, обладающая В унитарном коде только один разряд из множества может принимать значение 1 (или 0). Это означает, что двоичное число (в своем десятичном представлении) задает номер того выхода, на котором появится 1 (или 0, если выходы инверсные). Таблица истинности
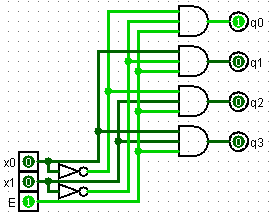
Функциональная схема
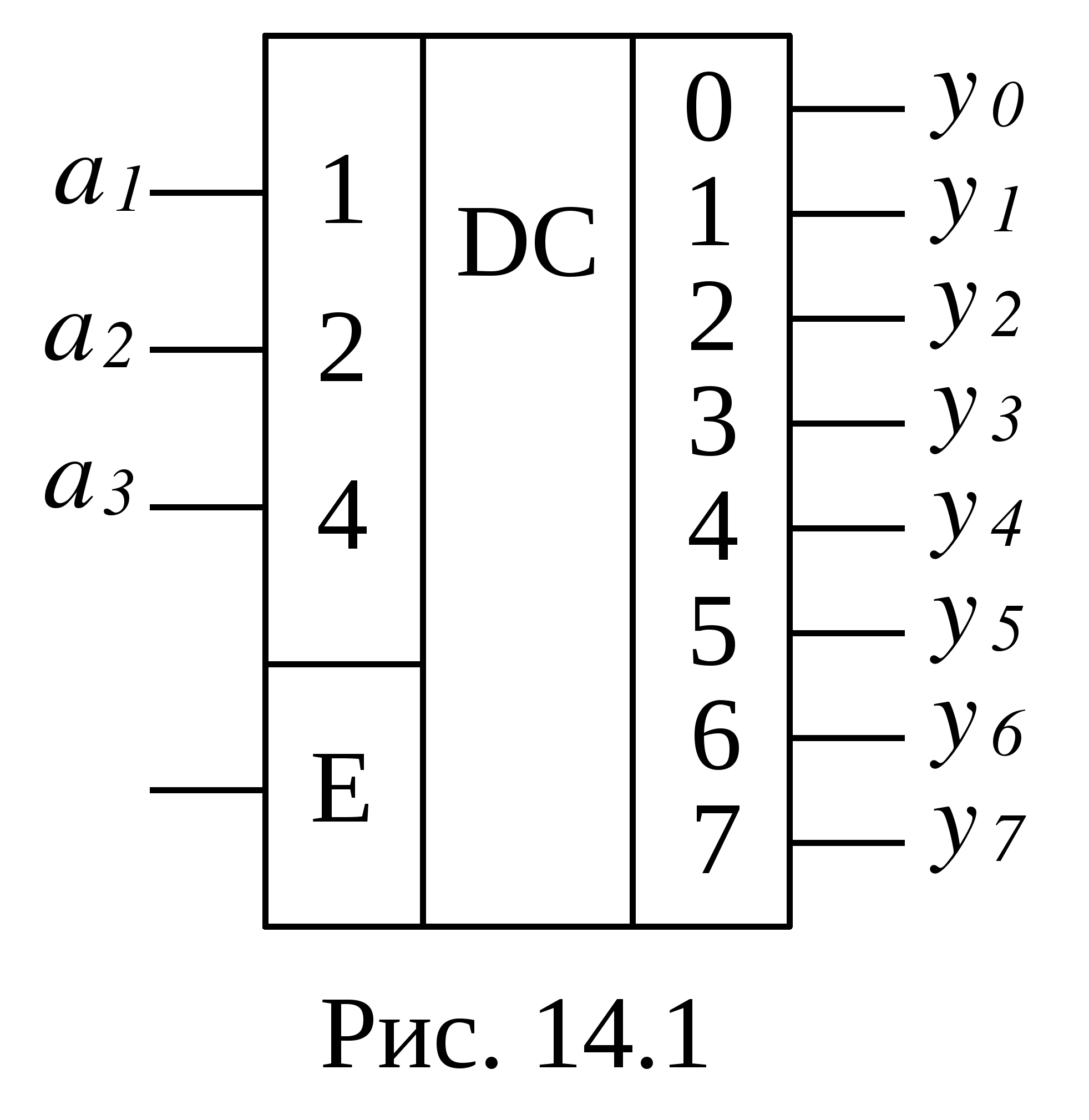
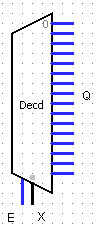
Условное графическое обозначение
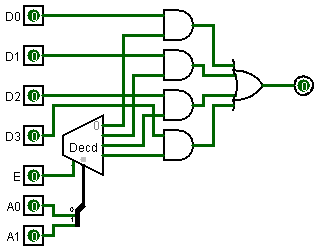
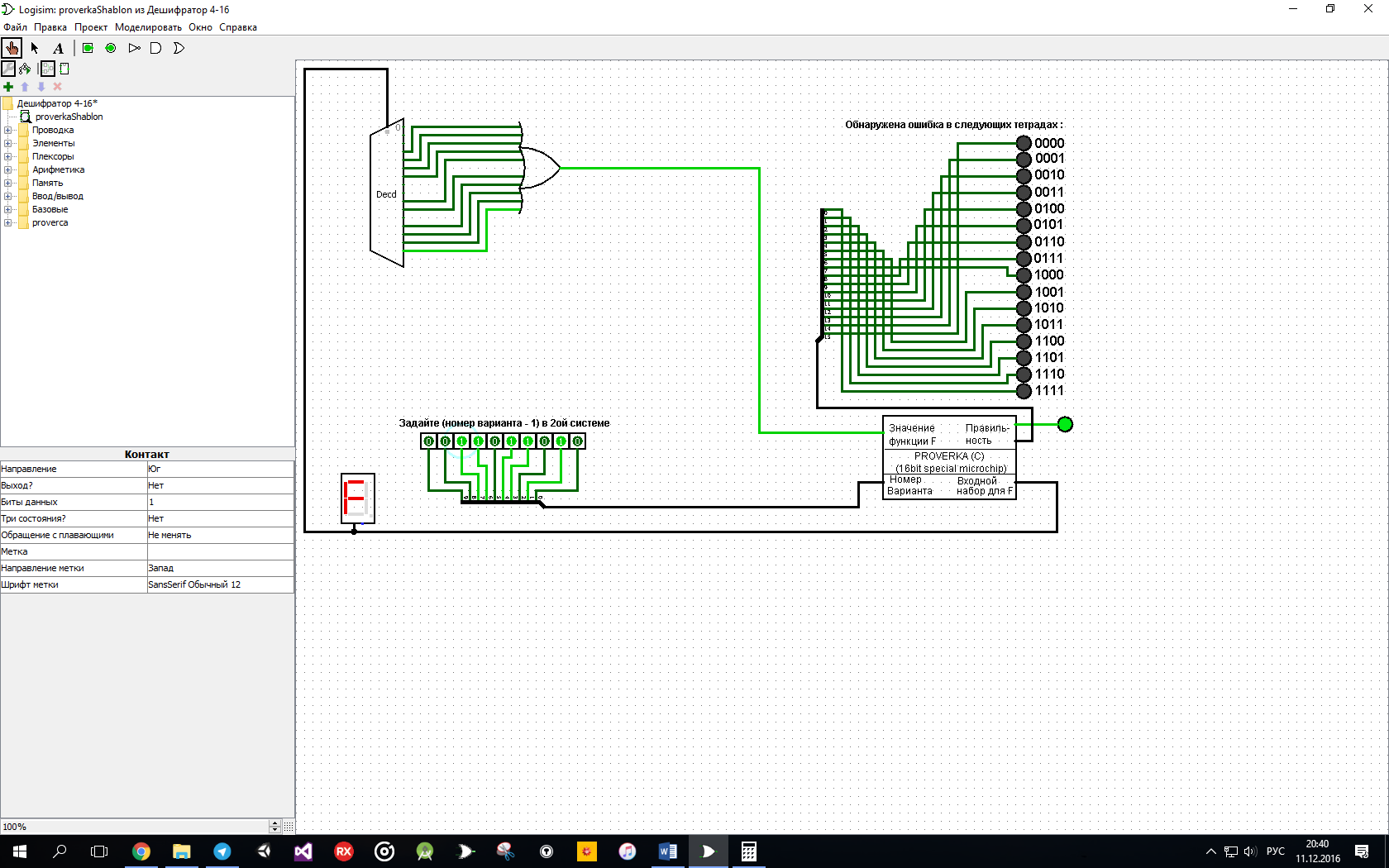
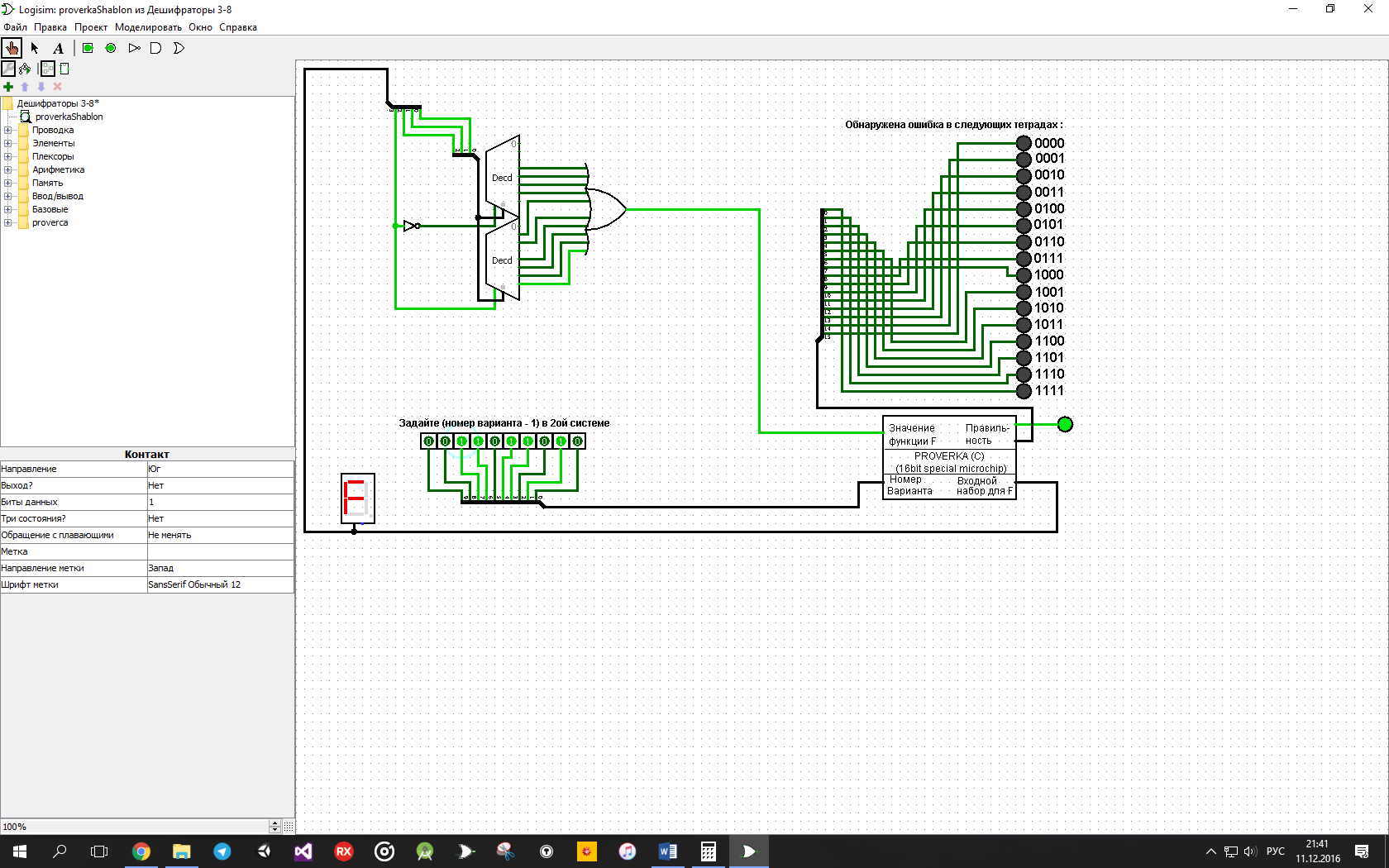
В зависимости от реализации входы и выходы могут быть как прямые, так и инверсные. Традиционное применение · В составе схем управления другими устройствами для последовательной подачи разрешающих сигналов; · В составе схем преобразователей кодов; · Для реализации логических функций. Реализация логической функции 4 переменных В данном примере используется функция
Мультиплексоры Мультиплексор – комбинационная схема, у которой имеется
Идея работы
· · · · Таблица истинности мультиплексора 4-1
Функциональная схема В основе мультиплексора лежит дешифратор.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-08-19; просмотров: 2831; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.69.162 (0.007 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

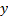
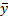
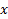
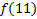
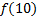
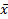
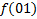
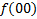
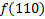
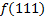
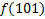
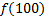
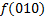
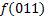
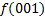
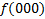
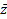
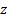
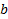
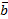
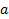
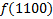
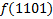
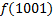
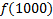
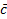
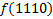
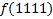
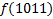
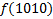
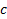
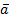
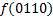
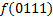
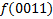
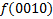
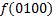
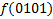
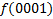
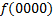
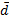
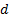
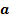
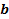

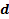
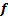
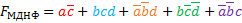
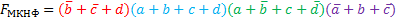
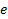
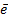
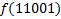
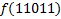
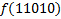
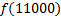
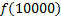
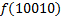
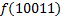
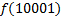
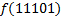
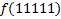
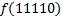
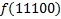
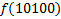
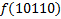
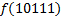
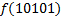
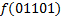
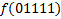
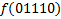
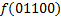
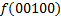
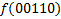
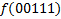
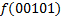
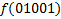
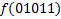
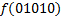
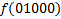
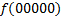
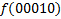
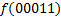
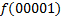

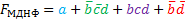
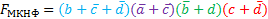
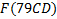 .
.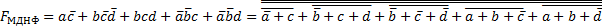
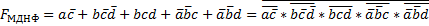
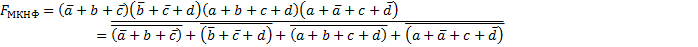
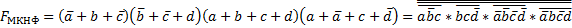
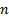 -адресными входами, одним разрешающим входом и
-адресными входами, одним разрешающим входом и 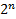 выходами. На адресные входы подается двоичное число, которое в своем десятичном представлении задает номер выхода, на котором формируется значащий сигнал. Предназначена для преобразования
выходами. На адресные входы подается двоичное число, которое в своем десятичном представлении задает номер выхода, на котором формируется значащий сигнал. Предназначена для преобразования 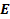
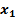
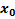
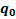
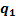
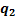
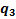
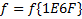 .
.
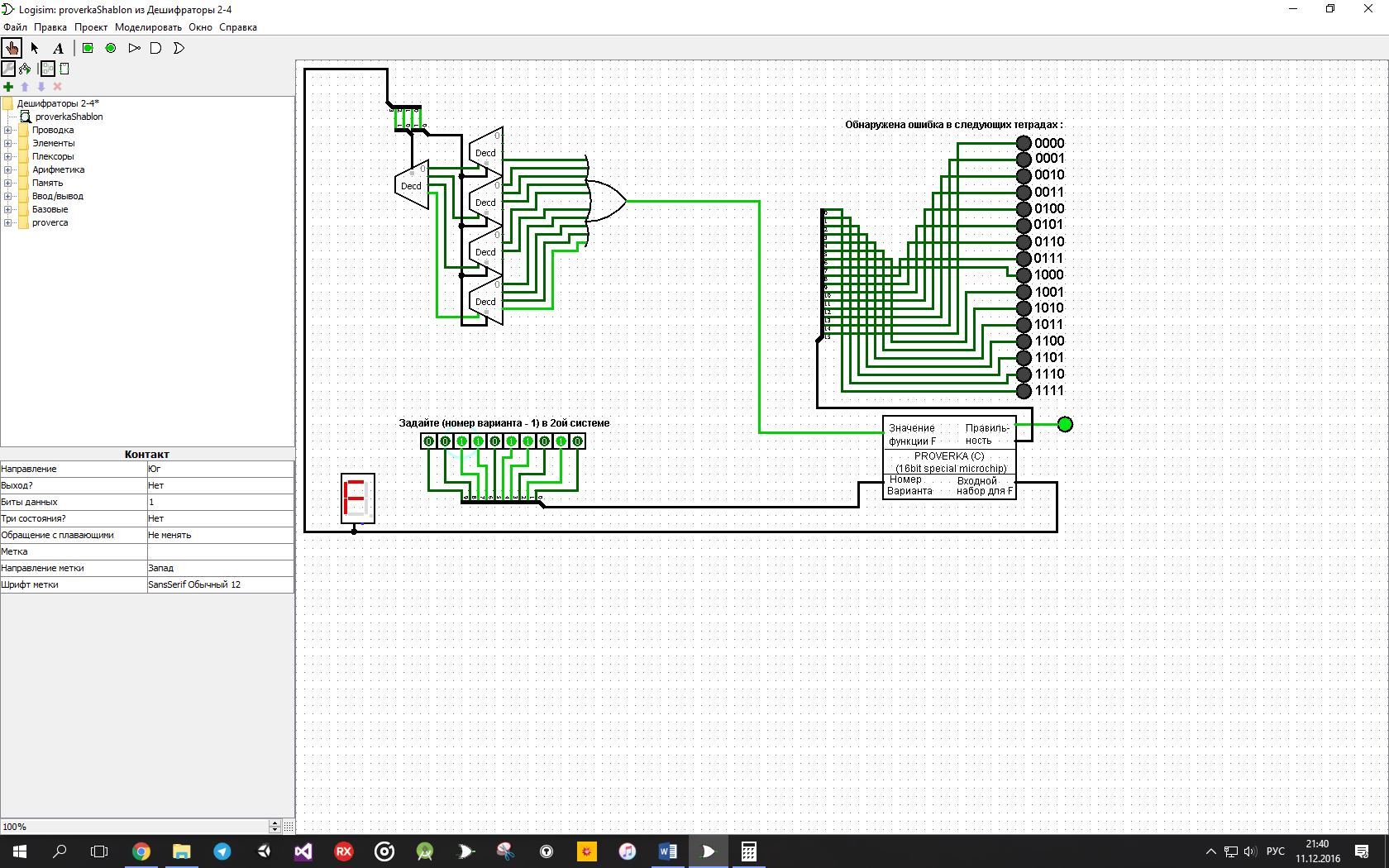
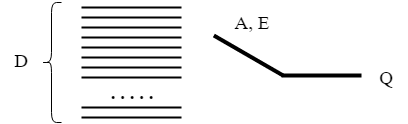 На данной схеме:
На данной схеме: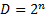 – информационные входы;
– информационные входы;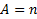 адресные входы;
адресные входы;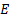 – разрешающий вход;
– разрешающий вход;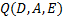 – результат на выходе.
– результат на выходе.