
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства бесконечно малых функций
1. Если функции 2. Произведение ограниченной при 3. Произведение постоянной на бесконечно малую функцию, есть функция бесконечно малая. 4. Произведение двух бесконечно малых функций, есть функция б/м. Определение. Функция Свойства бесконечно больших функций 1. Если 2. Если 3. Если 4. Если 5. Произведение двух бесконечно больших функций, есть функция бесконечно большая. Теоремы о пределах. Теорема 1. Для того чтобы число А было пределом функции Теореме 2. Предел постоянной величины равен самой этой постоянной, т.е. Теорема 3. Если функции Теорема 4. Постоянный множитель можно выносить за знак предела, т.е.
Теорема 5. Если для функции Следствие. Если функция Теоремы о пределах позволяют находить пределы функций, определяемых алгебраическими действиями над переменной, предел которой задан. В простейших случаях достаточно в выражение функции вместо переменной x подставить её предельное значение. Проверим правильность этого способа на примере. 1.3. Способы раскрытия неопределённостей вида 1. Если непосредственная подстановка в дробную функцию обращает числитель и знаменатель в нуль, то получаем неопределённость вида
Пример.
Для того чтобы сократить данную дробь, разложим числитель и знаменатель дроби на множители по формуле
Тогда исходный предел перепишем в виде:
2. Рассмотрим предел дроби, в знаменателе которой содержится иррациональная функция. Если при непосредственной подстановки в такую дробь предельного значения числитель и знаменатель обращаются в ноль, то для того чтобы раскрыть полученную неопределённость вида Пример. Домножим числитель и знаменатель дроби на выражение, сопряженное числителю (избавляемся от иррациональности в числителе):
= В данном примере выражением, сопряжённым знаменателю Замечание: Если делимое при 3. Рассмотрим частное двух функций Пусть в числителе и знаменателе некоторые многочлены. Тогда для раскрытия неопределённости необходимо каждое слагаемое числителя и знаменателя разделить на Пример.
Для того чтобы, раскрыть неопределенность вида
|
|||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.183.89 (0.009 с.) |
 и
и  - бесконечно малые функции, то их сумма
- бесконечно малые функции, то их сумма  +
+  функции на бесконечно малую, есть функция бесконечно малая.
функции на бесконечно малую, есть функция бесконечно малая.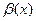 называется бесконечно большой (б/б), если для любого наперёд заданного сколь угодно малого положительного числа
называется бесконечно большой (б/б), если для любого наперёд заданного сколь угодно малого положительного числа  , найдётся такой номер
, найдётся такой номер  , зависящий от
, зависящий от  выполняется неравенство
выполняется неравенство  .
.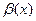 - бесконечно большая функция, то
- бесконечно большая функция, то 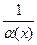 - функция бесконечно малая.
- функция бесконечно малая. - бесконечно малая функция не обращается в нуль, то
- бесконечно малая функция не обращается в нуль, то  - бесконечно большая функции, то их сумма
- бесконечно большая функции, то их сумма  при
при  , где
, где  .
. и
и  имеют пределы при
имеют пределы при  , то при
, то при 
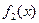 и, при условии
и, при условии  , частное
, частное  , причём
, причём 

 .
. , c=const.
, c=const. ,
,  в некоторой окрестности точки a выполняется неравенство
в некоторой окрестности точки a выполняется неравенство  и
и 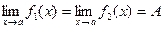 , то
, то  .
. .
. и
и 
 , это значит, что предельное значение в выражение функции можно подставлять только после предварительного сокращения данной дроби.
, это значит, что предельное значение в выражение функции можно подставлять только после предварительного сокращения данной дроби. =
= 

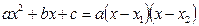 , где
, где  и
и 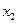 , это корни уравнения
, это корни уравнения  . Получим:
. Получим: и
и  .
. =
=  =
=  = - 9.
= - 9. =
=  .
. =
=  =
=  =
= =
=  =
=  .
. , является выражение вида
, является выражение вида  .
.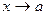 , конечно, а делитель стремится к нулю, то предел частного не существует и в этом случае говорят, что этот предел бесконечен, т.е.
, конечно, а делитель стремится к нулю, то предел частного не существует и в этом случае говорят, что этот предел бесконечен, т.е. 
 . Если при
. Если при  , числитель дроби
, числитель дроби 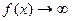 и знаменатель дроби
и знаменатель дроби  , то имеем неопределённость вида
, то имеем неопределённость вида  .
. в наивысшей степени из числа слагаемых числителя и знаменателя, а затем перейти к пределу.
в наивысшей степени из числа слагаемых числителя и знаменателя, а затем перейти к пределу. =
=  .
. надо под знаком предела числитель и знаменатель дроби разделить на переменную х с наивысшим показателем:
надо под знаком предела числитель и знаменатель дроби разделить на переменную х с наивысшим показателем: =
=  = [Осталось воспользоваться теоремами о пределах, а также тем, что функции
= [Осталось воспользоваться теоремами о пределах, а также тем, что функции  ,
,  и
и 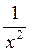 - бесконечно малые при х
- бесконечно малые при х  ]=
]=  =
=  .
.


