
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение производной. Зависимость между непрерывностью и дифференцируемостью функции
Определение. Производной функции Итак, по определению
Производная Рассматривая задачу о скорости, мы получили, что Если слово «скорость» понимать в более широком смысле, то можно производную функции Из рассмотренной задачи о касательной следует, что На основании ранее приведённых рассуждений получаем, что уравнение невертикальной касательной к кривой
Пример. Найти производную функции В этом случае
Следовательно, Основные правила дифференцирования. Таблица производных Дифференцирование функции (отыскание производных) непосредственно на основе определения производной оказывается практически неудобной процедурой. Нахождение производных значительно упрощается, если использовать общие правила дифференцирования, к рассмотрению которых мы переходим. Правила дифференцирования 1. Производная постоянной величины равна нулю.
2. Производная суммы функций (имеющих производные) равна сумме производных этих функций.
3. Постоянный множитель можно выносить за знак производной.
4. Производная произведения двух функций равняется сумме произведений производной первого множителя на второй и на производной второго множителя на первый.
5. Производная частного или дроби (при условии, что числитель и знаменатель дроби имеют производные и знаменатель в нуль не обращается) равняется разности произведений производной числителя на её знаменатель и производной знаменателя на числитель, делённой на квадрат знаменателя.
Таблица производных
|
|||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 222; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.192.219 (0.004 с.) |
 в точке
в точке  называется предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю, если этот предел существует и конечен. Производная функции
называется предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю, если этот предел существует и конечен. Производная функции 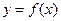 в точке
в точке  ,
,  или
или  ,
,  .
. . (7.1)
. (7.1) производная – число. В случаях, когда может возникнуть сомнение относительно переменной, по которой взята производная, эта переменная указывается в виде значка внизу:
производная – число. В случаях, когда может возникнуть сомнение относительно переменной, по которой взята производная, эта переменная указывается в виде значка внизу:  ,
,  .
. , т.е.
, т.е.  . Отсюда следует механический смысл производной: скорость
. Отсюда следует механический смысл производной: скорость  есть производная от пройденного пути
есть производная от пройденного пути  по времени
по времени  .
. по
по  в точке
в точке 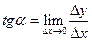 , т.е.
, т.е.  . Отсюда следует геометрический смысл производной: производная функции
. Отсюда следует геометрический смысл производной: производная функции  в точке
в точке 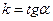 касательной в точке
касательной в точке  графика функции.
графика функции. можно записать в виде
можно записать в виде .
. .
.
 ,
,  .
. .
.







