
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Определение. Линейным дифференциальным уравнением второго порядка с постоянными коэффициентаминазывается уравнение вида
где Чтобы найти общее решение уравнения (12.1) надо знать два его частных решения Будем искать решение уравнения (12.1) в форме Так как
Уравнение (12.2) называют характеристическим уравнением исходного уравнения (12.1). Для его составления производные Решение уравнения (12.1) зависит от того, имеет ли соответствующее характеристическое уравнение (12.2) один корень, два корня или не имеет действительных корней. Рассмотрим три случая: 1) Пусть характеристическое уравнение (12.2) имеет два действительных корня
где 2) Если характеристическое уравнение (12.2) имеет один корень
где 3) Если характеристическое уравнение не имеет действительных корней (имеют мнимые корни), то общее решение уравнения (12.1) имеет вид:
Где Пример. Найти общее решение дифференциального уравнения второго порядка с постоянными коэффициентами: а). Решение: а). Составим характеристическое уравнение:
Тогда, общее решение дифференциального уравнения будет иметь вид
б). Составим характеристическое уравнение:
Тогда, общее решение дифференциального уравнения будет иметь вид:
в). Составим характеристическое уравнение:
Воспользуемся комплексным числом i, и представим дискриминант равный -36 как 36 i 2. Найдем Тогда, общее решение дифференциального уравнения будет иметь вид:
Таким образом, частное решение будет иметь вид
Примеры решения типовых задач
№ 1. Найти общее решение дифференциального уравнения Решение: Данное уравнение является линейным, так как содержит искомую функцию и ее производную в первой степени и не содержит их произведений. Применяем подстановку y = uv. Если y = uv, то
Так как искомая функция y представлена в виде произведения двух других неизвестных функций, то одну из них можно выбрать произвольно. Выберем функцию u так, чтобы выражение, стоящее в скобках левой части равенства (1), обращалось в нуль, то есть, чтобы имело место равенство Тогда уравнение (1) принимает вид: Уравнение (2) является уравнением с разделяющимися переменными относительно u и x. Решим его
Чтобы равенство (2) имело место, достаточно найти одно какое-либо частное решение, удовлетворяющее этому уравнению. Поэтому для простоты при интегрировании этого уравнения находим то частное решение, которое соответствует значению произвольной постоянной С=0. Подставив в (3) найденное выражение для u, получим
Интегрируя, имеем Теперь можно получить общее решение исходного уравнения Определим значение произвольной постоянной С при указанных начальных условиях
Таким образом, № 2. Найти общее и частное решение дифференциального уравнения второго порядка с постоянными коэффициентами
Решение: Составим характеристическое уравнение:
Тогда, общее решение дифференциального уравнения будет иметь вид
Найдем
Подставим начальные значения в выражения
|
|||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.9.115 (0.013 с.) |
 (12.1)
(12.1) и
и  - постоянные коэффициенты.
- постоянные коэффициенты. и
и 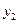 .
. , где
, где  - это некоторое действительное число.
- это некоторое действительное число. , то функция
, то функция 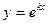 является решением уравнения (1), если
является решением уравнения (1), если  есть корень уравнения
есть корень уравнения . (12.2)
. (12.2) ,
,  , и функцию
, и функцию  заменим на
заменим на  в степени, соответствующей порядку производной.
в степени, соответствующей порядку производной. и
и  , причем
, причем  .. тогда общее решение уравнения (12.1) имеет вид:
.. тогда общее решение уравнения (12.1) имеет вид: , (12.3)
, (12.3) и
и  - некоторые числа.
- некоторые числа. , (12.4)
, (12.4) , (12.5)
, (12.5) - корни характеристического уравнения.
- корни характеристического уравнения. ; б).
; б).  ; в)
; в) 

 ;
;
 .
. .
. ;
;
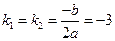 .
. .
.
 ;
; - действительных корней нет.
- действительных корней нет. и
и  :
: 

 .
. и частное решение, удовлетворяющее начальному условию y (0)=2.
и частное решение, удовлетворяющее начальному условию y (0)=2. . Подставляя y и y ’ в исходное уравнение, получим
. Подставляя y и y ’ в исходное уравнение, получим 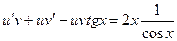 . Группируем первое и третье слагаемые и выносим v за скобку
. Группируем первое и третье слагаемые и выносим v за скобку
 (1).
(1). (2).
(2). (3).
(3).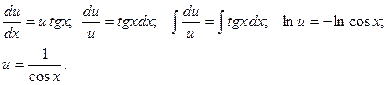

 .
. .
. .
. есть частное решение, удовлетворяющее данному начальному условию.
есть частное решение, удовлетворяющее данному начальному условию. .
.  ,
,  .
. ;
; 
 и
и  .
. .
.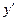 :
: .
. и
и  , получим систему двух уравнений с двумя неизвестными
, получим систему двух уравнений с двумя неизвестными  и
и  .
.


 .
. - частное решение.
- частное решение.


