
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Процессы с независимыми приращениями ⇐ ПредыдущаяСтр 7 из 7
Из определения процесса с независимыми приращениями вытекает (см. [2]), что любые его конечномерные распределения Для двух наиболее простых и, в то же время, наиболее важных представителей рассматриваемого класса с.п., а именно, винеровского и пуассоновского, можно указать простые алгоритмы моделирования. 5.1. Винеровский процесс. Рассмотрим винеровский процесс { wt, t ³ 0}, который, по определению, является процессом с независимыми гауссовыми приращениями: L(wt - ws) = N (0, s 2(t - s)) для любых 0 £ s < t. Для моделирования этого процесса на отрезке [0, T ] делят этот отрезок на n равных частей точками 0 = t0 < t1 <... < tn = T. Значения процесса wt в этих точках получают последовательно по формулам
где ni, i = 1,..., n - независимые стандартные гауссовы с.в. Для построения приближенной траектории винеровского процесса следует соединить отрезками прямых соседние полученные по формулам (18) точки траектории. Заметим, что выше (см. 3.2.) рассматривался другой способ (приближенного) моделирования винеровского процесса. 5.2. Однородный пуассоновский процесс. Этот процесс, часто называемый также простейшим потоком событий, является процессом с независимыми приращениями { pt, t ³ 0}, начинающимся из нуля и имеющим пуассоновские приращения: L(pt - ps) = П (l (t - s)) для любых 0 £ s < t. Параметр
где t 0 = 0, qk, k =1,2,... - независимые с.в. с функцией распределения
Процедура моделирования заканчивается, как только впервые tk превысит T. Смоделированная реализация будет кусочно-постоянной функцией, возрастающей единичными скачками в моменты tk Î T. 5.3. Неоднородный пуассоновский процесс. Так называют процесс с независимыми приращениями Xt, t ³ 0, начинающийся из нуля, приращения которого Xt - Xs для любых 0 £ s < t имеют пуассоновское распределение с параметром
где положительная ограниченная функция l (t), t ³ 0 называется мгновенной интенсивностью (в момент t) пуассоновского потока событий. Можно показать, что, как и в однородном случае, значения процесса Xt возрастают единичными скачками в случайные моменты времени t 1 < t 2 <... < t k <..., а в промежутках между соседними скачками остаются постоянными. При этом промежуток qk+1 = t k+1 - t k, k = 0,1,..., t 0 = 0 имеет закон распределения, зависящий от t k:
Как следует из (22), для того, чтобы промежутки между соседними скачками были с вероятностью 1 конечными, необходимо, чтобы мгновенная интенсивность l (t) удовлетворяла условию
Для моделирования неоднородного процесса Пуассона с интенсивностью l(t) на промежутке [0, T], очевидно, достаточно смоделировать моменты скачков по формулам (19), где величины q k теперь следует моделировать последовательно в соответствии с функцией распределения (22). Процедура моделирования останавливается, как только впервые tk превзойдет величину T. Величины q k+1 с распределением (22) можно моделировать с помощью "универсального метода" (см. гл. 1). При этом значение q k+1 получается как решение уравнения
Марковские процессы
6.1. Общие марковские процессы. Рассмотрим случайный процесс { X t, t Î T } со значениями в измеримом "фазовом" пространстве (E, e). Его называют марковским, если при любом фиксированном X s = x значения процесса X t, t > s не зависят от X u, u < s. Условную вероятность события { X t Î A Ì E} при условии X s = x называют переходной функцией (вероятностью) марковского процесса и обозначают P (s, x, t, A). Переходная функция для любых s < u < t удовлетворяет уравнению
называемому уравнением Чепмена-Колмогорова. Оно выражает важное свойство марковского процесса — отсутствие последействия: если известно состояние системы в некоторый момент времени u, то вероятности перехода из этого состояния не зависят от движения системы в моменты времени, предшествующие u. Если существует минимальный элемент t 0 множества T, то вероятности P 0(A) = P { Если существует неотрицательная функция p (s, x, t, y) такая, что
для всех s, x, A s < t, то ее называют переходной плотностью марковского процесса. Марковский процесс называется однородным, если его переходная вероятность зависит не от двух временных аргументов s и t, а только от их разности t - s:
Мы рассмотрим далее моделирование некоторых подклассов марковских процессов. 6.2. Цепи Маркова. Марковский процесс { X t, t Î T }, у которого дискретно как временное множество T, так и фазовое пространство E, называют цепью Маркова. В этом случае без потери общности можно считать, что
P (m, i, n, k) = pik (m, n). (26)
Определенная таким образом величина pik (m, n) называется переходной вероятностью цепи Маркова и представляет собой условную вероятность оказаться в k -том состоянии на n -м шаге при условии, что на m -том шаге (m < n) она находилась в состоянии i. Уравнение Чепмена-Колмогорова для переходной вероятности будет иметь вид
для любых m < r < n и i, k Î E. Если наряду с переходной вероятностью (26) задано также начальное распределение
p k = P { X 0 = k }, k = 0, 1,..., (28)
то будут определены и конечномерные распределения цепи Маркова: для любых n шагов с номерами m 1 < m 2 <... < m n и любых состояний ir Î E,
Моделирование значений
а последующие значения Моделирование цепи Маркова в частных случаях может упрощаться. Так для конечной цепи Маркова, у которой E = {0, 1,..., N}, суммы в правых частях формул (27) и (30) будут конечными. Соответственно, более простой будет и процедура моделирования, поскольку будут конечными как совокупности вероятностей начальных состояний, так и совокупности переходных вероятностей. Другое упрощение следует из однородности цепи Маркова, что выражается равенством pik (m, m + n) = pik (n) для любых m ³ 0, n ³ 1. Пользуясь уравнением Чепмена-Колмогорова, легко показать, что переходные вероятности однородной цепи Маркова за n шагов вполне определяются ее переходными вероятностями pik (1) = pik, i, k Î E за один шаг. Если
Разумеется, моделирование будет еще проще, когда однородная цепь Маркова является конечной. 6.3. Марковские процессы с непрерывным временем и дискретным фазовым пространством. Рассмотрим марковский процесс { Xt, t Î T }, у которого пространство состояний E = {0, 1,...} - конечно или счетно, а
P (s, i, s + t, k) = p ik (t) (31)
для любых i, k Î E и s ³ 0, t ³ 0. Будем также предполагать, что с вероятностью 1 реализации x t(w) рассматриваемого процесса непрерывны справа в каждой точке t ³ 0. Состояние i будем называть поглощающим, если p ii(t) = 1 для всех t > 0. Остальные состояния будем называть непоглощающими. Пусть t - момент первого выхода из начального состояния. Утверждение 1. Если начальное состояние X 0 = i является непоглощающим, t - момент выхода из начального состояния, то при некотором P i {t > t } = exp{-lit}, (32) где P i обозначает условную вероятность при условии X0 = i; при этом величины t и Xt независимы. Доказательство этого утверждения можно найти в [7]. Замечание 1. Для поглощающих состояний j будем считать l j = 0. Так как в этом случае для любого t P j {t > t } = 1, то формула (32) остается справедливой. Обозначим
P i {Xt = j } = p i (33)
и рассмотрим величины: t1 - момент выхода из начального состояния,
Утверждение 2. Величины Утверждение 2 позволяет описать поведение рассматриваемых марковских процессов. Имеется цепь Маркова
Процесс называется регулярным, если для всех i Î E
Таким образом, моделирование однородного марковского процесса с непрерывным временем и дискретным фазовым пространством сводится к моделированию вложенной однородной цепи Маркова, рассмотренному в предыдущем пункте настоящего параграфа, и моделированию последовательности независимых показательно-распределенных с.в. 6.4. Диффузионные марковские процессы. Так называется класс непрерывных марковских процессов, которые могут служить математической моделью явления диффузии - перемещения частицы под воздействием молекул среды, находящихся в хаотическом тепловом движении. Формально диффузионный марковский процесс можно определить через его переходную функцию. Пусть E - конечномерное евклидово пространство - фазовое пространство процесса X = { Xt, t ³ 0}; P (s, x, t, A) - его переходная функция. Прежде всего будем предполагать, что процесс X с вероятностью 1 имеет реализации без разрывов второго рода. Теперь сформулируем условия диффузионности: для x Î E, t ³ 0, e > 0 1) где V e(x) - шар радиуса e; 2) где a(t, x) - измеримая функция на [0,¥)´ E со значениями в E; 3) для всех z Î E
где (·,·) - скалярное произведение в E, B (t, x) - измеримая симметричная неотрицательно определенная матричная функция на [0,¥) ´ E, действующая из E в E. Функции a (t, x) и B (t,x) называются диффузионными коэффициентами процесса: a (t,x) - вектором (коэффициентом) переноса, B(t,x) - оператором (коэффициентом) диффузии. Условие 1) вместе с отсутствием разрывов 2-го рода является условием непрерывности процесса. Условие 2) указывает на наличие движения среды, в которой находится частица: частица из точки x в момент t за время h в среднем смещается на a (t,x) h. Условие 3) показывает, что матрица B (t,x) характеризует величину среднего квадратического отклонения частицы от ее положения x в момент t. Если среда изотропна (ее свойства одинаковы по всем направлениям), то B (t,x) = b 2(t,x) I, где b 2(t,x) - числовая функция, называемая коэффициентом диффузии, I - единичная матрица.
Далее для простоты будем рассматривать процессы в одномерном фазовом пространстве E = R1. Широкий класс диффузионных процессов с непрерывными коэффициентами образуют решения стохастических дифференциальных уравнений
dX t = a (t,Xt) dt + b (t, Xt) dw t, (34)
или, в интегральной форме,
Второй интеграл в правой части последнего уравнения, называемый стохастическим интегралом по винеровсому процессу { w t, t ³ 0} просто определяется в случае непрерывной зависимости подынтегрального процесса от s. Пусть непрерывный с вероятностью 1 случайный процесс { Yt, t ³ 0} согласован с винеровским процессом в следующем смысле: приращения wt - ws при t > s не зависят от совокупности случайных величин Yu, w u, u £ s. Тогда существует предел в смысле сходимости по вероятности интегральных сумм
при
Решением уравнения (35) с непрерывными по совокупности переменных коэффициентами a (t,x) и b (t,x) называется согласованный с винеровским процессом процесс { Xt, t ³ 0} с непрерывными траекториями, такой, что равенство (35) справедливо для всех t > 0 с вероятностью 1. Подробнее о стохастических интегралах и стохастических дифференциальных уравнениях см. [2].
Решения стохастических дифференциальных уравнений моделируются путем перехода к разностной схеме. Так, если процесс { Xt, t ³ 0} определяется уравнением (34), то простейшая разностная схема имеет вид
где k = 1, 2,... 0 = t 0 < t 1 <... < tk -1 < tk <.... Замечание 2. Попытки формального применения метода Рунге-Кутта с целью повышения точности моделирования решения стохастического дифференциального уравнения оказываются несостоятельными, поскольку винеровский процесс не обладает никакими производными.
Стационарные процессы
7.1. Общий подход к моделированию стационарных процессов. Мы рассматриваем здесь комплекснозначные процессы X = { Xt, t Î T }, у которых параметрическое множество T либо совокупность целых чисел {0, ±1, ±2,...} (случай дискретного времени), либо множество всех действительных чисел
то X называется стационарным в широком смысле. Употребляемый в дальнейшем без оговорок термин "стационарный" подразумевает стационарность в широком смысле. В рамках теории гильбертовых случайных процессов основными характеристиками стационарного процесса являются моментные функции первого и второго порядков, а именно среднее значение M Xt º m и корреляционная функция Теорема 2. Каждый стационарный процесс X допускает спектральное представление
в виде стохастического интеграла по комплекснозначному процессу с ортогональными приращениями Z. При этом корреляционная функция R(t) процесса X допускает представление
в виде интеграла Стилтьеса по неубывающей непрерывной слева функции ограниченной вариации F(w). Интегрирование в (37) и (38) производится в пределах -p £ w £ p в случае дискретного времени t, и в пределах -¥ < w < ¥ - в случае непрерывного t. Замечание 1. Функция F (w) в представлении (38) называется спектральной функцией процесса X. Она однозначно может быть восстановлена по корреляционной функции R (t). Особенно просто это делается в случае, когда F (w) абсолютно непрерывна. Тогда ее производная f (w) = dF (w)/dw называется спектральной плотностью процесса. В этом случае "формулы обращения" имеют вид
в случае дискретного времени и
в случае непрерывного времени. Замечание 2. Спектральная функция F (w) стационарного процесса X служит структурной функцией процесса с ортогональными приращениями Z, участвующего в представлении (37) процесса X:
для любых точек w1 < w2 спектра процесса X. Спектральное представление (37) стационарного процесса через процесс более простой структуры (процесс с ортогональными приращениями) можно положить в основу приближенного моделирования процесса X. Для этого разобьем интервал, в котором 0 < F (w) < F(+¥), на интервалы Dk и возьмем в Dk произвольную точку w k. Тогда, если Fk - приращение F (w) на интервале Dk, то можно записать:
и, следовательно
где { Zk } - ортогональные приращения процесса Z на интервалах { Dk }. Таким образом, формула (42) указывает алгоритм моделирования значений процесса X. Для работы этого алгоритма необходимо уметь моделировать процесс с ортогональными приращениями Z со структурной функцией F (w). Моделирование приращений Zk в формуле (42) возможно, в частности, когда Z является центрированным процессом с независимыми приращениями с заданным семейством двумерных распределений. Изложенный выше общий подход к моделированию стационарных процессов далеко не всегда удается реализовать на практике. Поэтому ниже мы рассмотрим частные случаи стационарных процессов, для которых задача моделирования решается в силу специфической структуры этих процессов. 7.2. Моделирование процесса с дробно-рациональной спектральной плотностью. Будем рассматривать одномерный стационарный гауссов процесс Xt с непрерывным временем, обладающий спектральной плотностью вида
где P (z) и Q(z) - многочлены от z с действительными коэффициентами:
причем m < n и нули Q(z) лежат в левой полуплоскости. Представление f (w) в виде (43) означает, что процесс Xt можно получить в виде линейной комбинации процесса Yt и m - 1 его производных:
где Yt является решением линейного стохастического дифференциального уравнения с постоянными коэффициентами
где w t, t ³ 0 - винеровский процесс. Если ввести вектор (столбец)
d V t = AV t dt + d W t, (46)
где
Заметим, что стационарное решение уравнения (45) имеет спектральную плотность
Если вектор V t будет найден, то значение процесса Xt находится по формуле (44) как линейная комбинация компонент вектора V t. Ниже излагается метод моделирования процесса Xt, предложенный Франклиным. Согласно уравнению (46), если известно значение процесса в момент t, то значение через промежуток времени D k определяется следующим образом:
где r (t) - гауссов случайный вектор,
Этот вектор некоррелирован со случайным вектором
Чтобы смоделировать r (t), нужно найти его корреляционную матрицу
R r =
где T - знак транспонирования, а
Можно показать, что R r удовлетворяет соотношению
откуда можно найти симметрическую матрицу R r. Следовательно, можем смоделировать гауссов вектор r (t) и получить очередное значение V t+ D t, а с ним, по (44), и значение процесса X. Чтобы смоделировать начальное значение процесса V 0, достаточно знать корреляционную матрицу в нуле:
Можно показать, что компоненты этой матрицы находятся по формуле
где k l можно определить из соотношений
и a 0 = 1. После нахождения матрицы K (0,0), гауссов вектор V 0 может быть смоделирован, как описано в гл.II, и по формуле (44) получается X 0. Последующие значения процесса V t, а следовательно, и процесса Xt, будут получаться по формулам (48) и (44) соответственно. 7.3. Случайные последовательности АРСС. Простота структуры случайных последовательностей авторегрессии и скользящего среднего (АРСС) и возможность использования их для аппроксимации широкого класса случайных последовательностей определяют как практический, так и теоретический интерес к ним. Моделирование этих последовательностей позволяет решать самые разнообразные прикладные задачи, связанные с изучением реальных процессов в науке и технике. Случайная последовательность (с. п.) АРСС с p вещественными параметрами авторегрессии b 1,..., bp и q вещественными параметрами скользящего среднего a 0 = 1, a 1,..., a q описывается уравнением
где Z = { Zt, t = 0, ±1, ±2,... } - последовательность некоррелированных, одинаково распределенных с.в. с M Zt = 0 D Zt =
лежат внутри единичного круга | z | < 1. Условие стационарности в дальнейшем предполагается выполненным. Умножая (49) на Xt-k и переходя к математическим ожиданиям, получаем
где RXZ (k) = M ZtXt-k. Так как Xt-k зависит только от членов входной последовательности до момента t - k, то очевидно, что RXZ (k) = 0 при k>0 и RXZ (k) ¹ 0 для k £ 0. Значения RXZ (k), k = 0, -1, -2,... находятся последовательно следующим образом. Умножим на Zt обе части равенства (49) и перейдем к математическим ожиданиям в полученном равенстве. В результате получаем RXZ (0) = Из (50) следует, что
Для решения разностных уравнений (51) (для больших k) в качестве начальных необходимы p значений, например, RX (q), RX (q - 1),..., RX (q - p + 1). Дисперсию
При моделировании с.п. АРСС(p,q) предполагаются известными (заданными) векторы параметров a и b, а также предполагается известным распределение величин Zk входной последовательности Z. Кроме того, величины входного случайного шума Zk обычно считаются независимыми, а не только некоррелированными. Для того, чтобы с помощью уравнения (49) можно было сразу начать моделирование стационарной последовательности, необходимы предварительные данные. Действительно, если на первом шаге (t = 1) мы хотим получить значение X1, являющееся элементом стационарной последовательности X, мы должны в формулу (49) подставить q + 1 значений входной последовательности: Z-q+ 1,..., Z 0, Z1 и p предшествующих X1 значений выходной последовательности: X-p+ 1,..., X -1, X 0. Следовательно, для начала процесса моделирования последовательности X нужно смоделировать случайный вектор
Это практически невозможно, если "шум" Z является негауссовым, поскольку невозможно найти распределение вектора U. Моделирование с.п. АРСС(p,q) в случае гауссова шума начинается с моделирования вектора (53). Поскольку на уравнение (49) можно смотреть как на линейное преобразование "шума" Z в выходной процесс X, то в случае гауссова шума, как известно, линейное преобразование не выводит за пределы гауссовой системы. Таким образом, вектор U будет гауссовым с нулевым средним и корреляционной матрицей R U, имеющей вид
где R Z - корреляционная матрица вектора Z q+1= (Z-q+ 1,..., Z 1) - это диагональная матрица, у которой диагональные элементы одинаковы и равны
и в результате имеем значение X 2 выходной последовательности. Процесс продолжается до получения "отрезка" стационарной с.п. АРСС(p,q) заданной длины.
|
|||||||||||
|
Последнее изменение этой страницы: 2019-04-30; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.218.146 (0.222 с.) |
 вполне определяются семейством двумерных распределений { Fts (x, y);
вполне определяются семейством двумерных распределений { Fts (x, y);  , i = 1,..., n (18)
, i = 1,..., n (18) , k =1, 2,... (19)
, k =1, 2,... (19) . (20)
. (20) , (21)
, (21) , 0 < x < ¥. (22)
, 0 < x < ¥. (22) . (23)
. (23) , где L(Uk) = R[0,1].
, где L(Uk) = R[0,1]. (24)
(24) Î A } для всех A Î e образуют так называемое начальное распределение процесса { X t, t Î T }. Начальное распределение и переходная функция марковского процесса вполне определяют его как процесс в широком смысле. Это значит, что при заданных начальном распределении и переходной функции марковского процесса, как отмечено в начале этой главы, есть принципиальная возможность его моделирования.
Î A } для всех A Î e образуют так называемое начальное распределение процесса { X t, t Î T }. Начальное распределение и переходная функция марковского процесса вполне определяют его как процесс в широком смысле. Это значит, что при заданных начальном распределении и переходной функции марковского процесса, как отмечено в начале этой главы, есть принципиальная возможность его моделирования.
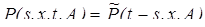 (25)
(25) (27)
(27) имеем
имеем
 (29)
(29)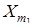 ,
,  ,...,
,...,  цепи Маркова сводится, таким образом, к моделированию случайного вектора с заданным законом распределения вероятностей: следует сначала смоделировать с.в.
цепи Маркова сводится, таким образом, к моделированию случайного вектора с заданным законом распределения вероятностей: следует сначала смоделировать с.в.  , k = 0, 1,..., (30)
, k = 0, 1,..., (30)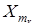 , 1 < r £ n, цепи - в соответствии с переходными (условными) вероятностями
, 1 < r £ n, цепи - в соответствии с переходными (условными) вероятностями  .
. - матрица переходных вероятностей за n шагов, а P =
- матрица переходных вероятностей за n шагов, а P =  - матрица переходных вероятностей за один шаг, то легко убедиться, что P (n) = P n, где в правой части стоит n -я степень матрицы P. Это значит, что однородная цепь Маркова как процесс в широком смысле вполне задается начальным распределением и переходными вероятностями за один шаг. Отсюда вытекает алгоритм моделирования последовательных значений цепи Маркова: X 0, X 1, X 2,.... Для получения значения с.в. X 0 моделируем дискретное распределение
- матрица переходных вероятностей за один шаг, то легко убедиться, что P (n) = P n, где в правой части стоит n -я степень матрицы P. Это значит, что однородная цепь Маркова как процесс в широком смысле вполне задается начальным распределением и переходными вероятностями за один шаг. Отсюда вытекает алгоритм моделирования последовательных значений цепи Маркова: X 0, X 1, X 2,.... Для получения значения с.в. X 0 моделируем дискретное распределение  , k = 0, 1,...}. Этот процесс продолжается до получения реализации цепи Маркова нужной "длины".
, k = 0, 1,...}. Этот процесс продолжается до получения реализации цепи Маркова нужной "длины". , t2 - время, которое процесс пробудет в состоянии
, t2 - время, которое процесс пробудет в состоянии  , q2 = t1 + t2,
, q2 = t1 + t2,  ,.... Если
,.... Если  , tn-1, qn-1 определены, то t n - время, которое процесс находится в состоянии
, tn-1, qn-1 определены, то t n - время, которое процесс находится в состоянии 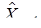 с момента qn-1 до выхода из этого состояния,
с момента qn-1 до выхода из этого состояния, =
=  .
. ,
,  даются равенством (33); условное распределение t1,...,tn при условии, что заданы
даются равенством (33); условное распределение t1,...,tn при условии, что заданы  совпадает с распределением n независимых показательно-распределенных с.в. с параметрами
совпадает с распределением n независимых показательно-распределенных с.в. с параметрами  .
.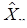 , n = 0, 1,..., называемая вложенной цепью Маркова, с вероятностями перехода за один шаг pij. Последовательные состояния
, n = 0, 1,..., называемая вложенной цепью Маркова, с вероятностями перехода за один шаг pij. Последовательные состояния  этой цепи определяют последовательные состояния процесса с непрерывным временем. Время пребывания процесса Xt в состоянии
этой цепи определяют последовательные состояния процесса с непрерывным временем. Время пребывания процесса Xt в состоянии 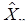 является показательно-распределенной величиной (при условии, что задано
является показательно-распределенной величиной (при условии, что задано  ) с параметром
) с параметром  и не зависит от времени пребывания в предыдущих состояниях. Таким образом, зная вложенную цепь Маркова, можно построить процесс Маркова с непрерывным временем до момента
и не зависит от времени пребывания в предыдущих состояниях. Таким образом, зная вложенную цепь Маркова, можно построить процесс Маркова с непрерывным временем до момента


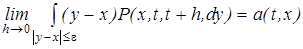 ,
, ,
, . (35)
. (35) , 0 = s 0 <... < sn = t
, 0 = s 0 <... < sn = t который называется стохастическим интегралом и обозначается символом
который называется стохастическим интегралом и обозначается символом .
.
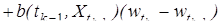 ,
,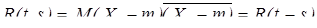 , (36)
, (36) процесса. Для простоты (и без потери общности) в дальнейшем считаем, что m = 0. Центральным результатом теории стационарных процессов является теорема А. Я. Хинчина о спектральном представлении процесса и его корреляционной функции.
процесса. Для простоты (и без потери общности) в дальнейшем считаем, что m = 0. Центральным результатом теории стационарных процессов является теорема А. Я. Хинчина о спектральном представлении процесса и его корреляционной функции. (37)
(37) , t Î T (38)
, t Î T (38) , w Î [-p,p] (39)
, w Î [-p,p] (39) , w Î (-¥,¥) (40)
, w Î (-¥,¥) (40) (41)
(41)
 , (42)
, (42) (43)
(43) ,
,  , a 0 = 1,
, a 0 = 1, , (44)
, (44) , (45)
, (45) , то уравнение (45) запишется в векторной форме
, то уравнение (45) запишется в векторной форме ,
, 
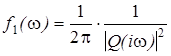 . (47)
. (47) , (48)
, (48) .
. .
. =
=  ,
,
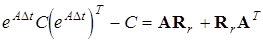 ,
, .
.
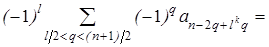

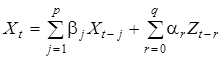 , (49)
, (49)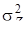 . Последовательность Z часто называют входной последовательностью или шумом. В дальнейшем с. п., задаваемую уравнением (49), будем обозначать АРСС(p,q). Существует обширная литература по теории с.п. АРСС. Необходимые для целей данного пособия факты теории процессов АРСС можно найти в [9]. В частности, известно, что с.п. АРСС(p,q) будет стационарной при условии, что все корни характеристического уравнения
. Последовательность Z часто называют входной последовательностью или шумом. В дальнейшем с. п., задаваемую уравнением (49), будем обозначать АРСС(p,q). Существует обширная литература по теории с.п. АРСС. Необходимые для целей данного пособия факты теории процессов АРСС можно найти в [9]. В частности, известно, что с.п. АРСС(p,q) будет стационарной при условии, что все корни характеристического уравнения
 , (50)
, (50) . Продолжая этот процесс, найдем необходимое число корреляционных моментов RXZ (k), k £ 0.
. Продолжая этот процесс, найдем необходимое число корреляционных моментов RXZ (k), k £ 0. , для k ³ q + 1 (51)
, для k ³ q + 1 (51)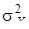 = RX (0) с.п. АРСС(p, q) вместе с RX (1),..., RX (p) получим, решая систему уравнений, получающихся из (50) при k = 0, 1, 2,..., p. Спектральная плотность с.п. АРСС(p, q) имеет вид
= RX (0) с.п. АРСС(p, q) вместе с RX (1),..., RX (p) получим, решая систему уравнений, получающихся из (50) при k = 0, 1, 2,..., p. Спектральная плотность с.п. АРСС(p, q) имеет вид , w Î [-p, p]. (52)
, w Î [-p, p]. (52) (53)
(53)
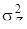 , R X - корреляционная матрица вектора X p = (X-p+ 1,..., X 0), элементы которой находятся из уравнений (50) и (51), а матрица R XZ размерности
, R X - корреляционная матрица вектора X p = (X-p+ 1,..., X 0), элементы которой находятся из уравнений (50) и (51), а матрица R XZ размерности



