
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Самарский государственный аэрокосмическийСтр 1 из 7Следующая ⇒
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени акад. С.П.КОРОЛЕВА А.Ф.Тараскин СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ и МЕТОД МОНТЕ-КАРЛО Учебное пособие САМАРА 1997 УДК 519.6 Статистическое моделирование и метод Монте-Карло: Учебное пособие/ А.Ф.Тараскин; Самар.гос.аэрокосм.ун-т. Самара, 1997. 62 с. ISBN 5-7883-0007-X
Изложены методы моделирования случайных величин, векторов и процессов. Предназначено для студентов специальности "Прикладная математика" при выполнении курсовых и расчетно-графических работ по курсам "Теория вероятностей и математическая статистика" и "Случайные процессы". Подготовлено на кафедре "Техническая кибернетика".
Библиогр.: 10 назв.
Печатается по решению редакционно-издательского совета Самарского государственного аэрокосмического университета имени академика С.П.Королева
Рецензенты: д-р физ.-мат. наук, проф. А.И.Жданов канд. физ.-мат. наук, доц. С.Я.Шатских
ISBN 5-7883-0007-X ÓТараскин А.Ф., 1997 ÓСамарский государственный аэрокосмический университет, 1997
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ...................................................................................... 4 1. МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН..................... 6
1. Моделирование дискретных случайных величин................ 6
2. Моделирование непрерывных случайных величин............ 10
2. МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВЕКТОРОВ................. 32
1. Моделирование вектора с независимыми координатами... 32
2. Универсальный метод моделирования непрерывных случайных векторов....................................... 34
3. Метод преобразований......................................................... 37
4. Моделирование гауссова вектора......................................... 39
5. Моделирование дискретных случайных векторов............... 40
3. МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ............. 41
1. Общие замечания................................................................... 41
2. Квазислучайные процессы.................................................... 42
3. Приближенное моделирование случайного процесса......... 44
4. Процессы с независимыми значениями................................ 46
5. Процессы с независимыми приращениями.......................... 47
6. Марковские процессы........................................................... 49
7. Стационарные процессы....................................................... 54
СПИСОК ЛИТЕРАТУРЫ............................................................. 61
ВВЕДЕНИЕ
Метод статистического моделирования, известный в литературе также под названием метода Монте-Карло, дает возможность конструировать для ряда важных задач алгоритмы, хорошо приспособленные к реализации на компьютерах. Возникновение метода Монте-Карло связывают обычно с именами Дж.Неймана, С.Улама, Н.Метрополиса, а также Г.Кана и Э.Ферми; все они в 40-х годах работали в Лос-Аламосе (США) над созданием первой атомной бомбы. Название "Монте-Карло" произошло от города Монте-Карло (княжество Монако), известного своими казино, ибо одним из простейших приборов для генерирования случайных чисел служит рулетка. Хотя общепринятого определения методов Монте-Карло не существует, тем не менее под этим названием подразумевают численные методы решения математических задач при помощи моделирования случайных величин и процессов. Основная идея метода -- связь между вероятностными характеристиками различных случайных процессов (вероятностями случайных событий или математическими ожиданиями случайных величин) и величинами, являющимися решениями задач математического анализа (значениями интегралов, решениями дифференциальных уравнений и т.п.). Оказывается, что вместо вычисления ряда сложных аналитических выражений можно "экспериментально" определить значения соответствующих вероятностей и математических ожиданий. Этот метод получил широкое развитие в связи с новыми возможностями, которые дают быстродействующие электронные вычислительные машины. Продемонстрируем суть метода на простейшей задаче. Пусть требуется приближенно определить математическое ожидание M X с.в. X. Пусть x1, x2,..., xn -- значения величины X, полученные при n независимых испытаниях (измерениях) с.в. X. Тогда величина
где Xk, k = 1,..., n -- независимые с.в. с общим распределением, совпадающим с распределением с.в. X, в соответствии с центральной предельной теоремой распределена по закону, близкому к гауссовому с параметрами
Поэтому имеет место оценка (с надежностью 0,997)
Таким образом, в этом случае "время" связано обратной зависимостью с достигаемой точностью e
Необходимо отметить одну особенность метода Монте-Карло, состоящую в том, что оценка погрешности вычислений имеет вероятностный характер. При этом методе нельзя утверждать, что ошибка не превысит какого-либо значения. Можно только указать границы, за которые ошибка не выйдет с вероятностью, близкой к единице. В частности, в оценке (2) эта вероятность равнялась 0,997. В соответствии с основной идеей метода Монте-Карло для приближенного вычисления величины a необходимо "придумать" такую с.в. X, чтобы M X = a. При этом сама величина X может быть функцией какой-то скалярной или векторной случайной величины, или даже функционалом от случайного процесса. Поэтому первоочередной задачей при использовании метода Монте-Карло является задача моделирования случайных величин или случайных процессов. Эта задача и рассматривается в настоящем пособии. Оно состоит из трех глав. Распределение материала по главам таково. В первой главе даются некоторые "прямые" и "специальные" методы моделирования случайных величин. Приводятся алгоритмы моделирования большого числа часто встречающихся в различных исследованиях дискретных и непрерывных с.в. Поскольку часть рассматриваемых с.в. студентам может встретиться впервые, в пособии приводятся попутно некоторые сведения о них. Во второй главе излагаются способы моделирования случайных векторов. Рассматривается моделирование вектора с независимыми координатами. В частности, приводятся равномерное распределение в параллелепипеде и гауссово распределение с независимыми координатами. Приводятся два общих метода моделирования векторов: так называемый универсальный метод и метод преобразований. С помощью последнего рассмотрено моделирование произвольного невырожденного гауссова вектора. Третья глава посвящена моделированию некоторых случайных процессов. В их числе квазислучайные процессы, процессы с независимыми значениями и независимыми приращениями. К последним относятся, в частности, винеровский процесс и процессы Пуассона. Рассмотрено моделирование основных классов марковских процессов, включая цепи Маркова, марковские процессы с непрерывным временем и дискретным фазовым пространством, а также диффузионные марковские процессы. Изложены методы моделирования стационарных процессов, среди которых подробно рассмотрены стационарные процессы с непрерывным временем, имеющие дробно-рациональную спектральную плотность, и стационарные случайные последовательности авторегрессии и скользящего среднего. Представлен также общий подход к приближенному моделированию процессов, основанный на их ортогональном разложении.
Общие замечания
Моделирование случайного процесса (с.п.) { Xt, t Î T } означает построения алгоритма, позволяющего получать его реализации { x t, t Î T }. В связи с приближенными вычислениями по методу Монте-Карло на ЭВМ могут быть использованы лишь реализации с.п. для некоторой последовательности значений аргумента, например, t 1,..., t n Î T.
Если случайный процесс изучается в рамках определения "в широком смысле", то это предполагает возможность задания его конечномерных распределений: для любого n ³ 1, любых t 1,..., t n Î T известна функция распределения F t_1...t_n(x 1,..., x n) вектора значений процесса Следует отметить два препятствия на пути осуществления намеченного выше подхода к моделированию с.п. Первое состоит в том, что далеко не всегда бывают заданы любые конечномерные распределения с.п. Второе $-$ в том, что даже если любые конечномерные распределения заданы, для больших n формирование реализаций случайного вектора становится громоздким и неудобным для использования на электронных цифровых вычислительных машинах. Эти обстоятельства заставляют использовать для моделирования либо специфические свойства процессов, относящихся к тем или иным классам случайных процессов, либо возможность представления данного процесса через более простые случайные элементы.
Квазислучайные процессы
Случайный процесс { Xt, t Î T } называется квазислучайным (иногда квазидетерминированным), если он представляется совокупностью функций времени заданного вида: Xt = S (t, Y), где Y = (Y 1,..., Y m) - векторный случайный параметр с множеством возможных значений? Ì R m. Каждой точке
xt = S (t; y), t Î T. (1)
Простейшим примером квазислучайного процесса является гармонический процесс со случайными амплитудой a, частотой w и фазой j:
Xt = S (t; a, w, j) = a cos (wt + j), (2)
причем векторный параметр Y = (a, w, j) принимает значения в области? трехмерного евклидова пространства, определяемой неравенствами: a > 0, В общем случае моделирование квазислучайного процесса сводится к
моделированию определяющего его случайного вектора Y. Получив одним из описанных в предыдущей главе методов значение этого вектора 2.1. Колебательные процессы со случайными параметрами. Во многих вопросах с.п. аппроксимируются суммой гармонических процессов с заданными частотами и случайными амплитудами и фазами. Иными словами, рассматриваются процессы вида
где wk - заданные числа, а величины ak и jk случайны. Теоретико-вероят- ностная структура этого процесса (как процесса в широком смысле) полностью определяется совместным распределением случайных величин Иногда целесообразно рассматривать комплекснозначные с.п. колебательного характера
где комплексные амплитуды gk являются случайными величинами:
gk = ak + i b k,
где ak, bk, k = 1,..., m - вещественные случайные величины. Ясно, что процесс Zt можно "расщепить" на вещественную и мнимую части, которые представляют собой колебательные процессы вида (3). Таким образом, колебательные процессы вида (3) или (4) представляют собой квазислучайные процессы, вполне определяемые 2 m -мерным случайным параметром. Их моделирование, как отмечено выше, сводится к моделированию случайного вектора (a 1,..., am, j 1,..., jm) в случае вещественного процесса (3) и вектора $(a 1,..., am, b 1,..., bm,) в случае комплексного процесса (4). Напомним, что колебательный процесс (4) является стационарным в широком смысле, если случайные амплитуды gk, k = 1,..., m обладают моментами до второго порядка включительно, причем M gk = 0, M 2.2. Линейная модель квазислучайного процесса. Еще один пример квазислучайного процесса дает так называемая линейная модель
где Y = (Y 1,..., Y m) - векторный случайный параметр, линейно входящий в правую часть (5), yk (t), k = 1,..., m - заданные функции. В ряде случаев изучаемый с.п. целесообразно аппроксимировать линейной моделью (5). Линейная модель может представлять собой частную сумму ряда в разложении некоторого случайного процесса. Для моделирования процесса (5) достаточно смоделировать случайный векторный параметр Y.
Марковские процессы
6.1. Общие марковские процессы. Рассмотрим случайный процесс { X t, t Î T } со значениями в измеримом "фазовом" пространстве (E, e). Его называют марковским, если при любом фиксированном X s = x значения процесса X t, t > s не зависят от X u, u < s. Условную вероятность события { X t Î A Ì E} при условии X s = x называют переходной функцией (вероятностью) марковского процесса и обозначают P (s, x, t, A). Переходная функция для любых s < u < t удовлетворяет уравнению
называемому уравнением Чепмена-Колмогорова. Оно выражает важное свойство марковского процесса — отсутствие последействия: если известно состояние системы в некоторый момент времени u, то вероятности перехода из этого состояния не зависят от движения системы в моменты времени, предшествующие u. Если существует минимальный элемент t 0 множества T, то вероятности P 0(A) = P {
Если существует неотрицательная функция p (s, x, t, y) такая, что
для всех s, x, A s < t, то ее называют переходной плотностью марковского процесса. Марковский процесс называется однородным, если его переходная вероятность зависит не от двух временных аргументов s и t, а только от их разности t - s:
Мы рассмотрим далее моделирование некоторых подклассов марковских процессов. 6.2. Цепи Маркова. Марковский процесс { X t, t Î T }, у которого дискретно как временное множество T, так и фазовое пространство E, называют цепью Маркова. В этом случае без потери общности можно считать, что
P (m, i, n, k) = pik (m, n). (26)
Определенная таким образом величина pik (m, n) называется переходной вероятностью цепи Маркова и представляет собой условную вероятность оказаться в k -том состоянии на n -м шаге при условии, что на m -том шаге (m < n) она находилась в состоянии i. Уравнение Чепмена-Колмогорова для переходной вероятности будет иметь вид
для любых m < r < n и i, k Î E. Если наряду с переходной вероятностью (26) задано также начальное распределение
p k = P { X 0 = k }, k = 0, 1,..., (28)
то будут определены и конечномерные распределения цепи Маркова: для любых n шагов с номерами m 1 < m 2 <... < m n и любых состояний ir Î E,
Моделирование значений
а последующие значения Моделирование цепи Маркова в частных случаях может упрощаться. Так для конечной цепи Маркова, у которой E = {0, 1,..., N}, суммы в правых частях формул (27) и (30) будут конечными. Соответственно, более простой будет и процедура моделирования, поскольку будут конечными как совокупности вероятностей начальных состояний, так и совокупности переходных вероятностей. Другое упрощение следует из однородности цепи Маркова, что выражается равенством pik (m, m + n) = pik (n) для любых m ³ 0, n ³ 1. Пользуясь уравнением Чепмена-Колмогорова, легко показать, что переходные вероятности однородной цепи Маркова за n шагов вполне определяются ее переходными вероятностями pik (1) = pik, i, k Î E за один шаг. Если Разумеется, моделирование будет еще проще, когда однородная цепь Маркова является конечной. 6.3. Марковские процессы с непрерывным временем и дискретным фазовым пространством. Рассмотрим марковский процесс { Xt, t Î T }, у которого пространство состояний E = {0, 1,...} - конечно или счетно, а
P (s, i, s + t, k) = p ik (t) (31)
для любых i, k Î E и s ³ 0, t ³ 0. Будем также предполагать, что с вероятностью 1 реализации x t(w) рассматриваемого процесса непрерывны справа в каждой точке t ³ 0. Состояние i будем называть поглощающим, если p ii(t) = 1 для всех t > 0. Остальные состояния будем называть непоглощающими. Пусть t - момент первого выхода из начального состояния. Утверждение 1. Если начальное состояние X 0 = i является непоглощающим, t - момент выхода из начального состояния, то при некотором P i {t > t } = exp{-lit}, (32) где P i обозначает условную вероятность при условии X0 = i; при этом величины t и Xt независимы. Доказательство этого утверждения можно найти в [7]. Замечание 1. Для поглощающих состояний j будем считать l j = 0. Так как в этом случае для любого t P j {t > t } = 1, то формула (32) остается справедливой. Обозначим
P i {Xt = j } = p i (33)
и рассмотрим величины: t1 - момент выхода из начального состояния, Утверждение 2. Величины Утверждение 2 позволяет описать поведение рассматриваемых марковских процессов. Имеется цепь Маркова
Процесс называется регулярным, если для всех i Î E
Таким образом, моделирование однородного марковского процесса с непрерывным временем и дискретным фазовым пространством сводится к моделированию вложенной однородной цепи Маркова, рассмотренному в предыдущем пункте настоящего параграфа, и моделированию последовательности независимых показательно-распределенных с.в. 6.4. Диффузионные марковские процессы. Так называется класс непрерывных марковских процессов, которые могут служить математической моделью явления диффузии - перемещения частицы под воздействием молекул среды, находящихся в хаотическом тепловом движении. Формально диффузионный марковский процесс можно определить через его переходную функцию. Пусть E - конечномерное евклидово пространство - фазовое пространство процесса X = { Xt, t ³ 0}; P (s, x, t, A) - его переходная функция. Прежде всего будем предполагать, что процесс X с вероятностью 1 имеет реализации без разрывов второго рода. Теперь сформулируем условия диффузионности: для x Î E, t ³ 0, e > 0 1) где V e(x) - шар радиуса e; 2) где a(t, x) - измеримая функция на [0,¥)´ E со значениями в E; 3) для всех z Î E
где (·,·) - скалярное произведение в E, B (t, x) - измеримая симметричная неотрицательно определенная матричная функция на [0,¥) ´ E, действующая из E в E. Функции a (t, x) и B (t,x) называются диффузионными коэффициентами процесса: a (t,x) - вектором (коэффициентом) переноса, B(t,x) - оператором (коэффициентом) диффузии. Условие 1) вместе с отсутствием разрывов 2-го рода является условием непрерывности процесса. Условие 2) указывает на наличие движения среды, в которой находится частица: частица из точки x в момент t за время h в среднем смещается на a (t,x) h. Условие 3) показывает, что матрица B (t,x) характеризует величину среднего квадратического отклонения частицы от ее положения x в момент t. Если среда изотропна (ее свойства одинаковы по всем направлениям), то B (t,x) = b 2(t,x) I, где b 2(t,x) - числовая функция, называемая коэффициентом диффузии, I - единичная матрица. Далее для простоты будем рассматривать процессы в одномерном фазовом пространстве E = R1. Широкий класс диффузионных процессов с непрерывными коэффициентами образуют решения стохастических дифференциальных уравнений
dX t = a (t,Xt) dt + b (t, Xt) dw t, (34)
или, в интегральной форме,
Второй интеграл в правой части последнего уравнения, называемый стохастическим интегралом по винеровсому процессу { w t, t ³ 0} просто определяется в случае непрерывной зависимости подынтегрального процесса от s. Пусть непрерывный с вероятностью 1 случайный процесс { Yt, t ³ 0} согласован с винеровским процессом в следующем смысле: приращения wt - ws при t > s не зависят от совокупности случайных величин Yu, w u, u £ s. Тогда существует предел в смысле сходимости по вероятности интегральных сумм
при
Решением уравнения (35) с непрерывными по совокупности переменных коэффициентами a (t,x) и b (t,x) называется согласованный с винеровским процессом процесс { Xt, t ³ 0} с непрерывными траекториями, такой, что равенство (35) справедливо для всех t > 0 с вероятностью 1. Подробнее о стохастических интегралах и стохастических дифференциальных уравнениях см. [2].
Решения стохастических дифференциальных уравнений моделируются путем перехода к разностной схеме. Так, если процесс { Xt, t ³ 0} определяется уравнением (34), то простейшая разностная схема имеет вид
где k = 1, 2,... 0 = t 0 < t 1 <... < tk -1 < tk <.... Замечание 2. Попытки формального применения метода Рунге-Кутта с целью повышения точности моделирования решения стохастического дифференциального уравнения оказываются несостоятельными, поскольку винеровский процесс не обладает никакими производными.
Стационарные процессы
7.1. Общий подход к моделированию стационарных процессов. Мы рассматриваем здесь комплекснозначные процессы X = { Xt, t Î T }, у которых параметрическое множество T либо совокупность целых чисел {0, ±1, ±2,...} (случай дискретного времени), либо множество всех действительных чисел
то X называется стационарным в широком смысле. Употребляемый в дальнейшем без оговорок термин "стационарный" подразумевает стационарность в широком смысле. В рамках теории гильбертовых случайных процессов основными характеристиками стационарного процесса являются моментные функции первого и второго порядков, а именно среднее значение M Xt º m и корреляционная функция Теорема 2. Каждый стационарный процесс X допускает спектральное представление
в виде стохастического интеграла по комплекснозначному процессу с ортогональными приращениями Z. При этом корреляционная функция R(t) процесса X допускает представление
в виде интеграла Стилтьеса по неубывающей непрерывной слева функции ограниченной вариации F(w). Интегрирование в (37) и (38) производится в пределах -p £ w £ p в случае дискретного времени t, и в пределах -¥ < w < ¥ - в случае непрерывного t. Замечание 1. Функция F (w) в представлении (38) называется спектральной функцией процесса X. Она однозначно может быть восстановлена по корреляционной функции R (t). Особенно просто это делается в случае, когда F (w) абсолютно непрерывна. Тогда ее производная f (w) = dF (w)/dw называется спектральной плотностью процесса. В этом случае "формулы обращения" имеют вид
в случае дискретного времени и
в случае непрерывного времени. Замечание 2. Спектральная функция F (w) стационарного процесса X служит структурной функцией процесса с ортогональными приращениями Z, участвующего в представлении (37) процесса X:
для любых точек w1 < w2 спектра процесса X. Спектральное представление (37) стационарного процесса через процесс более простой структуры (процесс с ортогональными приращениями) можно положить в основу приближенного моделирования процесса X. Для этого разобьем интервал, в котором 0 < F (w) < F(+¥), на интервалы Dk и возьмем в Dk произвольную точку w k. Тогда, если Fk - приращение F (w) на интервале Dk, то можно записать:
и, следовательно
где { Zk } - ортогональные приращения процесса Z на интервалах { Dk }. Таким образом, формула (42) указывает алгоритм моделирования значений процесса X. Для работы этого алгоритма необходимо уметь моделировать процесс с ортогональными приращениями Z со структурной функцией F (w). Моделирование приращений Zk в формуле (42) возможно, в частности, когда Z является центрированным процессом с независимыми приращениями с заданным семейством двумерных распределений. Изложенный выше общий подход к моделированию стационарных процессов далеко не всегда удается реализовать на практике. Поэтому ниже мы рассмотрим частные случаи стационарных процессов, для которых задача моделирования решается в силу специфической структуры этих процессов. 7.2. Моделирование процесса с дробно-рациональной спектральной плотностью. Будем рассматривать одномерный стационарный гауссов процесс Xt с непрерывным временем, обладающий спектральной плотностью вида
где P (z) и Q(z) - многочлены от z с действительными коэффициентами:
причем m < n и нули Q(z) лежат в левой полуплоскости. Представление f (w) в виде (43) означает, что процесс Xt можно получить в виде линейной комбинации процесса Yt и m - 1 его производных:
где Yt является решением линейного стохастического дифференциального уравнения с постоянными коэффициентами
где w t, t ³ 0 - винеровский процесс. Если ввести вектор (столбец)
d V t = AV t dt + d W t, (46)
где
Заметим, что стационарное решение уравнения (45) имеет спектральную плотность
|
||||||||||
|
Последнее изменение этой страницы: 2019-04-30; просмотров: 122; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.223.123 (0.218 с.) |
 , (1)
, (1) ,
, 
 . (2)
. (2) . (3)
. (3) . Задача формирования реализаций с.п. в этом случае ничем не отличается от задачи получения возможных значений n-мерного случайного вектора, рассмотренной в главе 2.
. Задача формирования реализаций с.п. в этом случае ничем не отличается от задачи получения возможных значений n-мерного случайного вектора, рассмотренной в главе 2. . Очевидно, что процесс (2), как процесс в широком смысле, задан, если задано распределение вероятностей вектора (a, w, j). При этом реализация гармонического процесса становится вполне определенной в соответствии с формулой (2) для всех t ³ 0, как только случайный вектор Y принимает одно из своих возможных значений, например,
. Очевидно, что процесс (2), как процесс в широком смысле, задан, если задано распределение вероятностей вектора (a, w, j). При этом реализация гармонического процесса становится вполне определенной в соответствии с формулой (2) для всех t ³ 0, как только случайный вектор Y принимает одно из своих возможных значений, например,  ,
,  , (3)
, (3) ,
,  = 0 для всех k, j = 1,..., m, k ¹ j.
= 0 для всех k, j = 1,..., m, k ¹ j. , t Î T (5)
, t Î T (5) (24)
(24) Î A } для всех A Î e образуют так называемое начальное распределение процесса { X t, t Î T }. Начальное распределение и переходная функция марковского процесса вполне определяют его как процесс в широком смысле. Это значит, что при заданных начальном распределении и переходной функции марковского процесса, как отмечено в начале этой главы, есть принципиальная возможность его моделирования.
Î A } для всех A Î e образуют так называемое начальное распределение процесса { X t, t Î T }. Начальное распределение и переходная функция марковского процесса вполне определяют его как процесс в широком смысле. Это значит, что при заданных начальном распределении и переходной функции марковского процесса, как отмечено в начале этой главы, есть принципиальная возможность его моделирования.
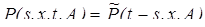 (25)
(25) (27)
(27) имеем
имеем
 (29)
(29)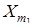 ,
,  ,...,
,...,  цепи Маркова сводится, таким образом, к моделированию случайного вектора с заданным законом распределения вероятностей: следует сначала смоделировать с.в.
цепи Маркова сводится, таким образом, к моделированию случайного вектора с заданным законом распределения вероятностей: следует сначала смоделировать с.в.  , k = 0, 1,..., (30)
, k = 0, 1,..., (30)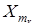 , 1 < r £ n, цепи - в соответствии с переходными (условными) вероятностями
, 1 < r £ n, цепи - в соответствии с переходными (условными) вероятностями  .
. - матрица переходных вероятностей за n шагов, а P =
- матрица переходных вероятностей за n шагов, а P =  - матрица переходных вероятностей за один шаг, то легко убедиться, что P (n) = P n, где в правой части стоит n -я степень матрицы P. Это значит, что однородная цепь Маркова как процесс в широком смысле вполне задается начальным распределением и переходными вероятностями за один шаг. Отсюда вытекает алгоритм моделирования последовательных значений цепи Маркова: X 0, X 1, X 2,.... Для получения значения с.в. X 0 моделируем дискретное распределение
- матрица переходных вероятностей за один шаг, то легко убедиться, что P (n) = P n, где в правой части стоит n -я степень матрицы P. Это значит, что однородная цепь Маркова как процесс в широком смысле вполне задается начальным распределением и переходными вероятностями за один шаг. Отсюда вытекает алгоритм моделирования последовательных значений цепи Маркова: X 0, X 1, X 2,.... Для получения значения с.в. X 0 моделируем дискретное распределение  , k = 0, 1,...}. Этот процесс продолжается до получения реализации цепи Маркова нужной "длины".
, k = 0, 1,...}. Этот процесс продолжается до получения реализации цепи Маркова нужной "длины". , t2 - время, которое процесс пробудет в состоянии
, t2 - время, которое процесс пробудет в состоянии  , q2 = t1 + t2,
, q2 = t1 + t2,  ,.... Если
,.... Если  , tn-1, qn-1 определены, то t n - время, которое процесс находится в состоянии
, tn-1, qn-1 определены, то t n - время, которое процесс находится в состоянии 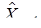 с момента qn-1 до выхода из этого состояния,
с момента qn-1 до выхода из этого состояния, =
=  .
. ,
,  даются равенством (33); условное распределение t1,...,tn при условии, что заданы
даются равенством (33); условное распределение t1,...,tn при условии, что заданы  совпадает с распределением n независимых показательно-распределенных с.в. с параметрами
совпадает с распределением n независимых показательно-распределенных с.в. с параметрами  .
.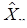 , n = 0, 1,..., называемая вложенной цепью Маркова, с вероятностями перехода за один шаг pij. Последовательные состояния
, n = 0, 1,..., называемая вложенной цепью Маркова, с вероятностями перехода за один шаг pij. Последовательные состояния  этой цепи определяют последовательные состояния процесса с непрерывным временем. Время пребывания процесса Xt в состоянии
этой цепи определяют последовательные состояния процесса с непрерывным временем. Время пребывания процесса Xt в состоянии 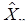 является показательно-распределенной величиной (при условии, что задано
является показательно-распределенной величиной (при условии, что задано  ) с параметром
) с параметром  и не зависит от времени пребывания в предыдущих состояниях. Таким образом, зная вложенную цепь Маркова, можно построить процесс Маркова с непрерывным временем до момента
и не зависит от времени пребывания в предыдущих состояниях. Таким образом, зная вложенную цепь Маркова, можно построить процесс Маркова с непрерывным временем до момента


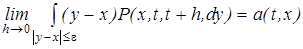 ,
, ,
, . (35)
. (35) , 0 = s 0 <... < sn = t
, 0 = s 0 <... < sn = t который называется стохастическим интегралом и обозначается символом
который называется стохастическим интегралом и обозначается символом .
.
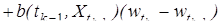 ,
,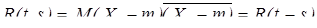 , (36)
, (36) процесса. Для простоты (и без потери общности) в дальнейшем считаем, что m = 0. Центральным результатом теории стационарных процессов является теорема А. Я. Хинчина о спектральном представлении процесса и его корреляционной функции.
процесса. Для простоты (и без потери общности) в дальнейшем считаем, что m = 0. Центральным результатом теории стационарных процессов является теорема А. Я. Хинчина о спектральном представлении процесса и его корреляционной функции. (37)
(37) , t Î T (38)
, t Î T (38) , w Î [-p,p] (39)
, w Î [-p,p] (39) , w Î (-¥,¥) (40)
, w Î (-¥,¥) (40) (41)
(41)
 , (42)
, (42) (43)
(43) ,
,  , a 0 = 1,
, a 0 = 1, , (44)
, (44) , (45)
, (45) , то уравнение (45) запишется в векторной форме
, то уравнение (45) запишется в векторной форме ,
, 
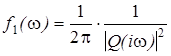 . (47)
. (47)


