Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование дискретных случайных величинСодержание книги
Поиск на нашем сайте
1.1. Универсальный метод моделирования дискретных случайных величин. Начнем с изложения общего подхода к моделированию дискретных случайных величин. Пусть X -- дискретная с.в. с множеством возможных значений c = { xi, i Î I }, где I = {0, 1, 2,...} -- конечное или счетное множество индексов, и вероятностями pi, i Î I, ее возможных значений:
pi =P(X = xi). (5) Совокупность вероятностей P = { pi, i Î I } удовлетворяет условиям
pi > 0 для всех i Î I.
и
Если U - с.в. с равномерным распределением R [0,1], то
где pi определено равенством (5). Сравнивая равенства (5) и (6), получаем алгоритм моделирования с.в. X: если величина U принимает значение
то величина X полагается равной xi. Перейдем к рассмотрению конкретных, и в то же время наиболее важных в теории и приложениях, дискретных случайных величин. 1.2. Схема независимых испытаний Бернулли, как известно, играет важнейшую роль в теории вероятностей. С другой стороны, она служит основой для моделирования целого ряда тесно связанных с ней с.в. Для моделирования последовательности испытаний Бернулли X1, X2,..., где L (Xk) = Bi (1,p): P(Xk = 1) = 1-P(Xk = 0) = p при заданном p Î (0,1), достаточно, очевидно, положить Xk = I (Uk £ p), k = 1, 2,..., где I (A) – индикатор случайного события A (I (A)=1, если A наступает, и 0 в противном случае). Событие A по традиции будем называть успехом. 1.3. Биномиальная с.в.. Чтобы смоделировать выборку для биномиальной с.в. X с параметрами (N,p) (т.е. L (X) = Bi (N,p)), достаточно воспользоваться свойством воспроизводимости распределения Bi (N,p) по параметру N:
X = X1 + X2 +... + XN,
где L (Xk) = Bi (1, p), k = 1, 2,..., N, и применить алгоритм схемы Бернулли. 1.4. Отрицательная биномиальная с.в. Отрицательная биномиальная с.в. X определяется через схему Бернулли как число всех "неудач" до r -го "успеха". Для закона распределения этой с.в. используют обозначение L (X) =
Подсчет показывает, что математическое ожидание и дисперсия отрицательной с.в. X даются равенствами
1.5. Геометрическая с.в. В частном случае r = 1 отрицательную биномиальную с.в. называют геометрической случайной величиной. Это будет с.в. X с законом распределения
P(X = j) = p (1 - p) j, j = 0, 1, 2,....
Иногда геометрическое распределение вероятностей называется распределением Фарри. Математическое ожидание и дисперсия этого распределения находятся по формулам
1.6. Случайная величина с распределением Паскаля определяется как число всех испытаний в схеме Бернулли до наступления r -того "успеха". Закон распределения Паскаля дается формулой
Между отрицательной биномиальной с.в. X и распределенной по закону Паскаля с.в. Y (при фиксированных r и p) имеет место простая связь Y = X + r. Отсюда имеем
Моделирование случайных величин с распределением Паскаля, геометрической и отрицательной биномиальной основывается на их определении и на алгоритме моделирования последовательности испытаний Бернулли. 1.7. Пуассоновская случайная величина X является одной из наиболее важных дискретных с.в. Она принимает свои значения из множества c = {0, 1,...} целых неотрицательных чисел, а закон распределения Пуассона задается формулой
где l > 0 -- параметр распределения. Закон распределения Пуассона с параметром l принято обозначать П(l). Как известно из курса теории вероятностей, математическое ожидание и дисперсия пуассоновской с.в. совпадают между собой и равны параметру ее распределения:
M X = l и D X = l.
Закон Пуассона является предельным для биномиального распределения и поэтому справедлива приближенная формула
где p мало, а n -- достаточно велико. По закону Пуассона часто распределено число случайных событий, происходящих в каком-либо промежутке времени (например, число распавшихся атомов радиоактивного вещества за единицу времени). Иногда закон Пуассона описывает не временные, а пространственные случайные явления. Тогда с.в. X трактуется как число точек, попавших в часть пространства заданного объема (например, число изюминок в булочке). Для моделирования пуассоновской с.в. можно использовать как универсальный метод, так и аппроксимирующую формулу (7). В последнем случае следует выбрать достаточно большое n и положить Ниже, при рассмотрении непрерывных с.в., мы укажем еще один способ моделирования пуассоновских с.в.
Приведем еще два, важных с точки зрения приложений, примера дискретных с.в., для моделирования которых можно воспользоваться описанным выше универсальным методом. 1.8. Гипергеометрическая с.в. Пусть в множестве N элементов содержится k элементов с признаком B. Из множества извлекаются случайным образом n элементов (n £ N) без возвращения. Тогда число X элементов с признаком B, содержащихся в выборке, подчиняется гипергеометрическому закону распределения вероятностей. Вероятность появления в выборке из n элементов ровно x с признаком B определяется формулой
в которой 0 £ x £ min(n, k) £ N. Эта формула и задает так называемое гипергеометрическое распределение вероятностей, определяемое тремя параметрами N, n, k, и обозначаемое Hg (N, n, k). Подсчет математического ожидания и дисперсии гипергеометрической с.в. X приводит к формулам
1.9. Равномерно распределённая дискретная с.в. X -- это с.в. с конечным множеством возможных значений c = { xi, i Î I }, принимаемых с одинаковыми вероятностями. Если множество c состоит из N элементов, то
Равномерный закон дискретной с.в., таким образом, определяется одним параметром N и обозначается Ud (N). С.в. X с равномерным распределением Ud (N) имеет математическое ожидание
и дисперсию
|
||||||
|
Последнее изменение этой страницы: 2019-04-30; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.125.137 (0.007 с.) |

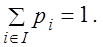
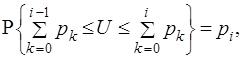 (6)
(6)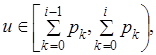
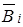 (r, p). При этом
(r, p). При этом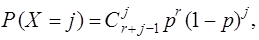 j = 0, 1, 2,....
j = 0, 1, 2,....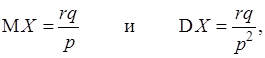 где q = 1 - p.
где q = 1 - p.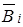 (1, p), для которого
(1, p), для которого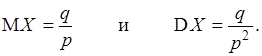
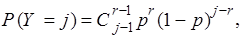 j = r, r + 1,...
j = r, r + 1,...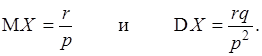
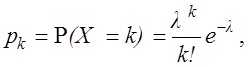 pk Î c
pk Î c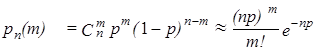 (7)
(7)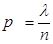 . В этом случае, согласно (7), биномиальное распределение Bi (n,
. В этом случае, согласно (7), биномиальное распределение Bi (n,  ) будет близко к пуассоновскому П(l).
) будет близко к пуассоновскому П(l).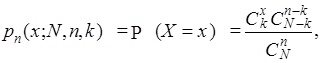 (8)
(8)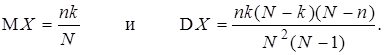
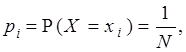 для любого i Î I (9)
для любого i Î I (9)