
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Универсальный метод моделирования непрерывных случайных векторовСодержание книги
Поиск на нашем сайте
Если X= (X1,..., Xn) - непрерывный случайный вектор, то его плотность можно представить в виде произведения условных плотностей распределения вероятностей этих величин:
f X (x1,..., xn) = f1(x1)f2(x2|x1)f_3(x3|x1,x2)... fn(xn|x1,..., xn-1 ) Все условные плотности распределения в правой части этого равенства выражаются через совместную плотность f X(x 1,..., xn). Приведем эти выражения:
....
Введем условные функции распределения
Тогда будет справедливо следующее утверждение, которое мы приводим без доказательства. Утверждение 1. Пусть U1,..., Un - независимые одинаково распределенные по закону R(0,1) случайные величины. Тогда случайный вектор
имеет плотность распределения вероятностей f X(x 1,..., x n). Замечание 1. Уравнения (7) имеют единственные решения, если эти решения находятся по формулам (3). Представление плотности f X(x 1,..., x n) в форме произведения условных плотностей координат вектора X возможно n! способами. В частности, при n=2
f X (x 1, x 2) = f 1(x 1) f 2(x 2| x 1) = f 2(x 2) f 1(x 1 | x 2).
Разным произведениям соответствуют разные порядки "разыгрывания" с.в. X 1, X 2,..., X n и, вообще говоря, разные уравнения (7). Приводимый ниже пример показывает, что иногда удачный выбор порядка позволяет упростить эти уравнения. Если X 1,..., X n независимы, то все их условные распределения равны безусловным:
F k(x k | x 1,..., x k-1) = F k(x k), k = 1,2,..., n,
и порядок разыгрывания величин не играет роли. Уравнения (7) превращаются в уравнения
F k(X k) = U k, k = 1,2,..., n
и приводят к решению (2). Пример 1. Рассмотрим случайную точку (X,Y), которая принимает значения в треугольнике x + y < 1, x > 0, y > 0 с плотностью f (x, y) = 6 x. а) Выберем в качестве первой величины X. Тогда
Соответствующие этим плотностям функции распределения будут:
FX (x) = 3 x 2 - 2 x 3 при 0 < x < 1,
Из формул (7) получаем уравнения для последовательного моделирования X и Y:
3 X 2 - 2 X 3 = U 1, Y = U 2 (1 - X).
б) Выберем теперь в качестве первой величины Y. Тогда
Соответствующие функции распределения будут:
F Y(y) = 1- (1 - y)3 при 0 < y < 1,
Согласно (7), используя 1 - U 1 вместо U 1, получим уравнения для последовательного моделирования Y и X:
(1 - Y)3 = U 1, X 2= U 2(1 - Y)2.
Сравним оба алгоритма для моделирования X и Y в первом из них для нахождения X необходимо решать кубические уравнения, в то время как во втором можно использовать явные формулы
Замечание 2. Часто вместо представления f (x,y) = f 1(x) f 2(y | x) пишут аналогичное по форме представление F (x,y) = FX (x) FY (y | x), которое на самом деле неверно. Так в рассмотренном примере в треугольнике F (x,y) = 3 x 2 y, а
Из утверждения 1 следует, что моделирование случайного вектора может быть сведено к последовательному моделированию его координат. Для этого достаточно применить "универсальный" метод, разрешая последовательно уравнения (7) и помня при этом, что при необходимости (отсутствие единственного решения) следует пользоваться формулой (3). Таким образом, мы получаем метод моделирования непрерывного случайного вектора, который, как и в случае скалярной с.в., называют " универсальным " или стандартным. Практическое использование универсального метода моделирования случайного вектора часто связано с весьма громоздкими вычислениями, и в некоторых случаях для моделирования с.в. X k с условной плотностью 3. Метод преобразований В предыдущей главе при рассмотрении моделирования гауссовых с.в. было доказано важное общее Утверждение 2. о взаимно однозначном дифференцируемом преобразовании случайных векторов. Такое преобразование можно интерпретировать как переход к новым координатам, а упомянутое Утверждение 2. дает правило преобразования плотности при преобразовании координат. Во многих случаях таким путем удается упростить формулы моделирования случайных векторов. 3.1. Равномерное распределение в шаре
Однако плотности распределения каждой из координат достаточно громоздки. Поэтому перейдем к сферическим координатам:
В новых координатах шар переходит в параллелепипед
то в новых координатах плотность распределения случайного вектора (R, Q, F) (или точки P) имеет вид
и, следовательно, сферические координаты точки P независимы. Уравнения для их моделирования можно записать так:
Отсюда (см. формулы (2)) получаем формулы
по которым легко находятся и декартовы координаты точки P:
3.2. Выбор случайного направления в пространстве. Говоря о "случайном" направлении подразумевают выбор случайного направления в условиях, когда все направления в трехмерном пространстве равновозможны. Направление условимся характеризовать единичным вектором Выбор случайного направления можно трактовать как равномерное распределение конца единичного радиуса-вектора на поверхности сферы единичного радиуса. Таким образом, нас интересует единичный вектор X такой, что для любого телесного угла
где Легко видеть, что если P - случайная точка, равномерно распределенная в шаре равны, и вероятности того, что точка P попадет в каждый из них, одинаковы. Поэтому из (8) получаем формулы для выбора "случайного" направления:
Используя формулы, связывающие декартовы координаты со сферическими, получаем алгоритм моделирования вектора X = (X1, X2, X3):
|
||||||
|
Последнее изменение этой страницы: 2019-04-30; просмотров: 214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.116.142 (0.011 с.) |

 ,
,




 (7)
(7) при 0 < x < 1;
при 0 < x < 1;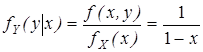 при 0 < y < 1 - x.
при 0 < y < 1 - x. при 0 < y < 1 - x.
при 0 < y < 1 - x. при 0 < y < 1,
при 0 < y < 1,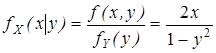 при 0 < x < 1 - y.
при 0 < x < 1 - y. при 0 < x < 1 - y.
при 0 < x < 1 - y. ,
,  .
. ,
,  .
.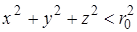 . Обозначим через X, Y, Z декартовы координаты точки P. Их совместная плотность распределения в шаре постоянна:
. Обозначим через X, Y, Z декартовы координаты точки P. Их совместная плотность распределения в шаре постоянна:
 ,
, 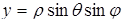 ,
, 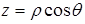
 ,
, 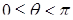 ,
,  . Так как якобиан преобразования будет
. Так как якобиан преобразования будет ,
, ,
, ,
, 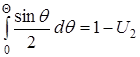 ,
,  .
. ,
,  ,
,  (8)
(8)


 .
.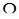 с вершиной в начале координат
с вершиной в начале координат ,
, обозначает величину телесного угла
обозначает величину телесного угла  , то направление ее радиуса-вектора обладает нужным нам свойством. Действительно, если
, то направление ее радиуса-вектора обладает нужным нам свойством. Действительно, если  1 и
1 и  2 - два равных по величине телесных угла, то объемы соответствующих им шаровых секторов
2 - два равных по величине телесных угла, то объемы соответствующих им шаровых секторов ,
,  .
.
 , X 3 = 2 U1 - 1
, X 3 = 2 U1 - 1


