
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели поршневого вытеснения нефти водойСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Показатели, близкие к реальным, получают в ряде случаев при расчете разработки нефтяных месторождений с помощью модели, состоящей из моделей процесса поршневого вытеснения нефти водой и слоистого пласта. Прежде всего, рассмотрим процесс поршневого вытеснения нефти водой из одного прямолинейного слоя (пропластка) толщиной
Рис.45. Модель прямолиней-ного пропластка при поршневом вытеснении нефти водой
Пусть давление воды, входящей слева в пропласток, равно Предположим, что в заводненной зоне, т. е. при
Дифференцируя это выражение по времени t, получим следующую формулу для расхода воды, поступающей в i-й пропласток:
С другой стороны, можно, согласно обобщенному закону Дарси, т. е. с учетом того, что фазовые проницаемости для воды и нефти соответственно составляют
где При рассмотрении процессов вытеснения нефти водой принимают, что нефть и вода — несжимаемые жидкости. Сжимаемость пород пласта также не учитывают. Поэтому, аналогично формуле (5.13), можно написать для дебита нефти, получаемой из того же i-го пропластка, выражение
где Из выражений (5.13) и (5.14), исключая из них давление
Приравнивая (5.12) и (5.15), получим следующее дифференциальное уравнение относительно
Интегрируя (5.16) и учитывая, что
Решая это квадратное уравнение, получаем окончательные формулы для определения
Для того чтобы получить формулу для определения времени Тогда
Из формулы (5.19) следует, что пропласток с очень большой проницаемостью обводнится в самом начале процесса вытеснения нефти водой из слоистого пласта. Рассмотрим процесс вытеснения нефти водой из слоистого пласта. Для удобства сложим мысленно все пропластки этого пласта в один «штабель», причем таким образом, чтобы абсолютная проницаемость пропластков изменялась последовательно начиная с наименьшей и кончая самой высокой. Пусть, например, в нижней части этого «штабеля» расположен пропласток с самой большой проницаемостью, а вверху – с наименьшей проницаемостью. Согласно вероятностно-статистической модели слоисто-неоднородного пласта, суммарную толщину
где Формулу (5.20) можно представить в дифференциальном виде, т. е. через плотность распределения, следующим образом:
Здесь Вытеснение нефти водой из слоистого пласта в целом можно рассматривать и иным образом, считая, что в некоторые слои толщиной
С учетом (5.21) из (5.22), заменяя конечные приращения соответствующих величин их дифференциалами и опуская индекс
Согласно модели поршневого вытеснения, из обводнившихся пропластков нефть не извлекается – из них поступает только вода. Обводняются, конечно, в первую очередь высокопроницаемые пропластки. В используемых в теории разработки нефтяных месторождений моделях пластов могут быть слои с бесконечно большой проницаемостью. Таким образом, к моменту времени
Дебит воды
С помощью приведенных формул можно, задаваясь последовательно значениями времени Приведенные выкладки и формулы пригодны, как уже было указано, для случаев, когда в течение всего процесса вытеснения нефти водой из слоистого пласта перепад давления не изменяется. Когда же задано условие постоянства расхода Введем функцию
Из формулы (5.15), если ее записать относительно дифференциалов расхода
Как и в случае постоянного перепада давления, при постоянном расходе закачиваемой в слоистый пласт воды к некоторому моменту времени
Обучающемуся предлагается следующая процедура последовательного определения Дебит нефти находят по формуле
а дебит воды — по формуле
В радиальном случае при поршневом вытеснении нефти водой из отдельного слоя вместо уравнения (5.12) будем иметь
Пусть в некоторый момент времени фронт вытеснения нефти водой в
В области
Из (5.32) и (5.33)
Аналогично (5.12) для i-го пропластка
Приравнивая правые части (5.34) и (5.35) и опуская индекс
Обозначим
Теперь можно найти время
Из формулы (5.34)
Интегрируя (5.39), как и для прямолинейного случая, при
Для вычисления интеграла (5.40) в подынтегральное выражение следует подставить
Необходимо задаваться величиной
|
|||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 776; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.008 с.) |

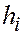 и длиной
и длиной  , пористостью
, пористостью 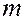 и проницаемостью
и проницаемостью 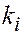 (рис. 45).
(рис. 45).
 , а давление воды на выходе из него
, а давление воды на выходе из него  . Будем считать, что в течение всего процесса вытеснения нефти водой из слоя перепад давления
. Будем считать, что в течение всего процесса вытеснения нефти водой из слоя перепад давления 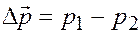 постоянный. В соответствии с моделью поршневого вытеснения нефти водой остаточная нефтенасыщенность в заводненной области слоя остается постоянной, равной
постоянный. В соответствии с моделью поршневого вытеснения нефти водой остаточная нефтенасыщенность в заводненной области слоя остается постоянной, равной  . Согласно рис. 45, фронт вытеснения занимает в момент времени t положение
. Согласно рис. 45, фронт вытеснения занимает в момент времени t положение 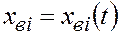 . Ширина пропластка, измеряемая в направлении, перпендикулярном к плоскости чертежа (см. рис. 45), равная ширине всего пласта, составляет
. Ширина пропластка, измеряемая в направлении, перпендикулярном к плоскости чертежа (см. рис. 45), равная ширине всего пласта, составляет  . При постоянном перепаде давления на входе в пропласток и на выходе из него расход закачиваемой воды
. При постоянном перепаде давления на входе в пропласток и на выходе из него расход закачиваемой воды  будет изменяться со временем.
будет изменяться со временем. cвязанная вода с начальной насыщенностью
cвязанная вода с начальной насыщенностью  полностью смешивается с закачиваемой водой, так что условно (см. рис. 45) заводненная область насыщена остаточной нефтью и этой смесью. Тогда суммарный объем воды
полностью смешивается с закачиваемой водой, так что условно (см. рис. 45) заводненная область насыщена остаточной нефтью и этой смесью. Тогда суммарный объем воды  , вошедший в область пропластка при
, вошедший в область пропластка при 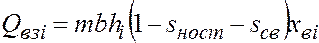 (5.11)
(5.11) . (5.12)
. (5.12) ,
,  (
(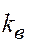 и
и  — постоянные относительные проницаемости), получить для расхода воды следующее выражение:
— постоянные относительные проницаемости), получить для расхода воды следующее выражение: , (5.13)
, (5.13) — вязкость воды.
— вязкость воды. , (5.14)
, (5.14) — вязкость нефти.
— вязкость нефти. на фронте вытеснения, получим
на фронте вытеснения, получим , (5.15)
, (5.15) .
.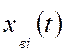 :
: . (5.16)
. (5.16) при t=0 приходим к следующему квадратному уравнению относительно
при t=0 приходим к следующему квадратному уравнению относительно  :
: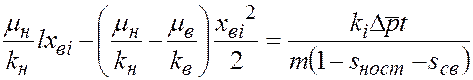 . (5.17)
. (5.17)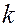 в любой момент времени
в любой момент времени ;
; . (5.18)
. (5.18) обводнения
обводнения 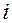 -го пропластка с проницаемостью
-го пропластка с проницаемостью 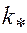 , положим в первой формуле (5.18)
, положим в первой формуле (5.18)  .
. . (5.19)
. (5.19) пропластков, проницаемость самого проницаемого которых не ниже, чем некоторое значение, равное
пропластков, проницаемость самого проницаемого которых не ниже, чем некоторое значение, равное  , (5.20)
, (5.20) — общая толщина всех пропластков в «штабеле».
— общая толщина всех пропластков в «штабеле». . (5.21)
. (5.21) — плотность вероятностно-статистического распределения абсолютной проницаемости.
— плотность вероятностно-статистического распределения абсолютной проницаемости. и проницаемостью
и проницаемостью  . Тогда из формул (5.17) и (5.18)
. Тогда из формул (5.17) и (5.18) (5.22)
(5.22)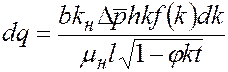 . (5.23)
. (5.23) , когда обводнятся все слои с проницаемостью
, когда обводнятся все слои с проницаемостью  , можно добывать нефть лишь из слоев с проницаемостью
, можно добывать нефть лишь из слоев с проницаемостью  . В соответствии со сказанным для дебита нефти из рассматриваемого слоистого пласта на основе (5.23) получим следующее выражение:
. В соответствии со сказанным для дебита нефти из рассматриваемого слоистого пласта на основе (5.23) получим следующее выражение: . (5.24)
. (5.24)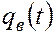 можно определить также с учетом указанных соображений по формуле
можно определить также с учетом указанных соображений по формуле . (5.25)
. (5.25) ,
,  и
и  .
. закачиваемой в слоистый пласт воды, получают несколько иные соотношения для определения дебитов нефти и воды, а также перепада давления, который в данном случае будет изменяться с течением времени. Если
закачиваемой в слоистый пласт воды, получают несколько иные соотношения для определения дебитов нефти и воды, а также перепада давления, который в данном случае будет изменяться с течением времени. Если  , справедливы формулы (5.15) и (5.16), следует при этом учитывать, что перепад давления
, справедливы формулы (5.15) и (5.16), следует при этом учитывать, что перепад давления  — функция времени, т. е.
— функция времени, т. е.  .
.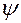 :
: ,
,  . (5.26)
. (5.26)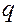 и толщины пласта
и толщины пласта  . (5.27)
. (5.27) часть слоев окажется полностью обводненной и из них будет добываться только вода, из другой, же части будут добывать безводную нефть. Поэтому полный расход закачиваемой во всю толщу слоистого пласта воды
часть слоев окажется полностью обводненной и из них будет добываться только вода, из другой, же части будут добывать безводную нефть. Поэтому полный расход закачиваемой во всю толщу слоистого пласта воды  можно определить в результате интегрирования выражения (5.27) и прибавления к правой его части интеграла, учитывающего приток воды из обводнившихся слоев. Имеем
можно определить в результате интегрирования выражения (5.27) и прибавления к правой его части интеграла, учитывающего приток воды из обводнившихся слоев. Имеем . (5.28)
. (5.28)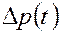 . Вначале следует задаться значением проницаемости
. Вначале следует задаться значением проницаемости  , по формуле (5.19) определить время обводнения слоя
, по формуле (5.19) определить время обводнения слоя  вычислить
вычислить  . Затем определяют интегралы, входящие в формулу (5.28), и
. Затем определяют интегралы, входящие в формулу (5.28), и  при заданном
при заданном  , (5.29)
, (5.29)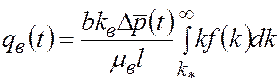 . (5.30)
. (5.30)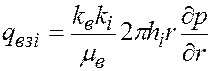 . (5.31)
. (5.31) -м слое дошел до радиуса
-м слое дошел до радиуса  , где пластовое давление равно
, где пластовое давление равно  . Тогда интегрируя (5.31) от радиуса скважины до радиуса
. Тогда интегрируя (5.31) от радиуса скважины до радиуса  , получим
, получим . (5.32)
. (5.32) , т.е. впереди фронта вытеснения, движется нефть с тем же расходом
, т.е. впереди фронта вытеснения, движется нефть с тем же расходом 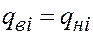 , так что аналогично (5.32) имеем
, так что аналогично (5.32) имеем . (5.33)
. (5.33) ;
;  . (5.34)
. (5.34) . (5.35)
. (5.35) , получим
, получим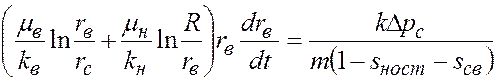 . (5.36)
. (5.36) и проинтегрируем (5.36) при
и проинтегрируем (5.36) при  Тогда
Тогда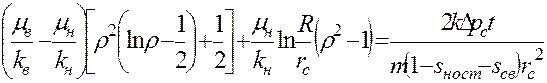 . (5.37)
. (5.37) . Полагая
. Полагая  , получим
, получим
 (5.38)
(5.38) . (5.39)
. (5.39) имеем
имеем ; (5.40)
; (5.40) из формулы (5.37). Поэтому в общем случае
из формулы (5.37). Поэтому в общем случае  необходимо определять, по-видимому, численным путем с использованием ЭВМ. Однако, как и в прямолинейном случае, при
необходимо определять, по-видимому, численным путем с использованием ЭВМ. Однако, как и в прямолинейном случае, при  вычисления упрощаются. Выражение (5.40) превращается в следующую формулу:
вычисления упрощаются. Выражение (5.40) превращается в следующую формулу: . (5.41)
. (5.41) . (5.42)
. (5.42) по формуле (5.38) и в соответствии с известным вероятностно-статистическим законом распределения абсолютной проницаемости определять
по формуле (5.38) и в соответствии с известным вероятностно-статистическим законом распределения абсолютной проницаемости определять 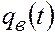 .
.


