
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель пласта с модифицированнымиСодержание книги
Поиск на нашем сайте
относительными проницаемостями.
Если принять, что фазовая проницаемость для воды зависит от остаточной нефтенасыщенности
то расход воды
где Формула (3.4) справедлива в предположении, что в обводнившемся слое нефть вытесняется мгновенно по модели поршневого вытеснения до насыщенности
Если к рассматриваемому моменту времени обводнились слои общей толщиной
При отсутствии остаточной нефти расход воды через обводнившиеся слои будет
Учитывая, что распределение проницаемости по слоям описывается каким-либо вероятностно-статистическим законом, модифицированную относительную проницаенмость можно представить в виде: для воды для нефти где Модифицированную водонасыщенность пласта определяют по отношению объема связанной воды и воды, внедрившейся в слои, к поровому объему пласта:
Модифицированные относительные проницаемости для воды и нефти представляют соответственно доли воды и нефти в общей производительности всех слоев. В общем случае они пропорциональны обводненности и содержанию нефти в добываемой жидкости. Описанную модель приближают к реальной, рассматривая процесс непоршневого вытеснения нефти водой для каждого слоя. Анализируя характер обводнения продукции скважин, можно построить характеристику обводнения пласта и, решая обратную гидродинамическую задачу, уточнить модифицированные проницаемости, т. е. адаптировать модель к реальному процессу. В этом случае модифицированные показатели интегрально отражают все особенности реального пласта и процессов, происходящих при их разработке.
Модели вытеснения нефти
Рассмотрим модели процесса вытеснения нефти водой (газом). 3.2.1. Модель поршневого вытеснения.
Предполагается движущийся в пласте вертикальный фронт (границы), впереди которого нефтенасыщенность равна начальной ( 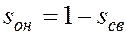 ), а позади остается промытая зона с остаточной нефтенасыщенностью ), а позади остается промытая зона с остаточной нефтенасыщенностью  . На рис. 25 схематически показан профиль насыщенности при . На рис. 25 схематически показан профиль насыщенности при
фиксированном положении фронта Рис. 25. Модель поршневого вытеснения нефти водой. Насыщенность: 1- водой; 2 – нефтью В соответствии с этой моделью полное обводнение продукции скважин должно произойти мгновенно в момент подхода фронта вытеснения к скважинам. Модель непоршневого вытеснения
По схеме Бакли — Леверетта предполагается в пласте движущийся фронт вытеснения. Скачок нефтенасыщенности на нем значительно меньше, чем при поршневом вытеснении. Рис. 26. Модель непоршневого вытеснения нефти водой Насыщенность: 1- водой; 2 – нефтью Перед фронтом вытеснения движется только нефть, позади него — одновременно нефть и вода со скоростями, пропорцио-нальными соответствующим фазовым проницаемостям. Причем по мере продвижения фронта вытеснения скорости изменяются не только в зависимости от насыщенности в пласте, но и во времени. В момент подхода фронта к скважине происходит мгновенное обводнение до некоторого значения, соответствующего скачку нефтенасыщенности на фронте Уравнение неразрывности
Выведем вначале уравнение неразрывности массы вещества при его одномерном прямолинейном движении в пласте. Масса
Рис. 27. Схема элементарного объема прямолинейного пласта Рис. 28. Схема элементарного пласта в трехмерном случае
Если считать, что в элемент пласта через его левую грань поступает вещество с массовой скоростью
Из (3.12) имеем
при
Уравнение (3.14) и есть уравнение неразрывности массы вещества в пласте при одномерном прямолинейном движении насыщающего его вещества. Чтобы получить такое уравнение для трехмерного случая, необходимо рассмотреть баланс массы в объемном элементе пласта
Уравнение (3.15) можно записать также в следующем общем виде:
Уравнения (3.15), (3.16) — уравнения неразрывности массы вещества во время его движения при трехмерном измерении. Если в пласте одновременно движутся несколько веществ, находящихся как в газовой, так и в жидкой фазе, составляют уравнения неразрывности массы каждого вещества (компонента) в соответствующих фазах.
Уравнение энергии Полная энергия единицы массы пласта
Из закона сохранения энергии или, точнее, из первого начала термодинамики следует, что изменение энергии пласта
или с учетом (3.17)
Дадим количественную оценку входящих в (3.19) величин. Удельная внутренняя энергия пласта
где
где Тогда для изменения удельной кинетической энергии получим
Из приведенной оценки следует, что удельной кинетической энергией движущихся в пласте веществ можно всегда, кроме особых случаев движения веществ в призабойной зоне скважин, пренебречь. Если изменение удельной потенциальной энергии движущегося в пласте вещества составляет даже 100 м, то при умножении этой величины на
где Поровый объем пласта остается, вообще говоря, неизменным, поскольку не изменяются геометрия пласта и его пористость. Работа вещества в пласте связана всегда с его расширением. Поэтому в (3.21) и введена величина Тогда
Подставляя (3.22) в (3.21) получим
Оценим возможную работу вещества, насыщающего пласт. Очевидно, что наибольшую работу может производить в пласте газ. Для простоты оценки будем считать газ идеальным, для которого
Пусть при снижении давления Тогда
Сделанная оценка показывает, что работа вещества, насыщающего пласт, хотя и намного меньше, чем изменение удельной внутренней энергии при тепловых методах разработки нефтяных месторождений, все же при определенных условиях„ как это показывает опыт, может быть значительной. Рассмотрим вопрос о том, чему равняется входящая в (3.18) и (3.19) величина
Допустим, что в пласте движется газ вязкостью
В сутки из килограмма движущегося в пласте газа будет выделяться Напишем уравнение сохранения энергии в пласте, учитывая теплопроводность и конвекцию, а также работу расширения- сжатия веществ и гидравлическое трение. Рассматривая, как и при выводе уравнения неразрывности массы фильтрующегося в пласте вещества, поток внутренней энергии
Здесь
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 460; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.011 с.) |

 , (3.3)
, (3.3) , поступающей в слой толщиной
, поступающей в слой толщиной  , определим по формуле
, определим по формуле , (3.4)
, (3.4)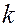 - абсолютная проницаемость слоя;
- абсолютная проницаемость слоя;  - ширина слоя;
- ширина слоя;  - длина слоя;
- длина слоя; 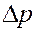 - перепад давления на расстоянии
- перепад давления на расстоянии  - вязкость воды.
- вязкость воды. . Если в слое
. Если в слое  . (3.5)
. (3.5) , то при
, то при  суммарный расход воды
суммарный расход воды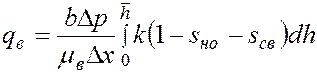 (3.6)
(3.6) . (3.7)
. (3.7)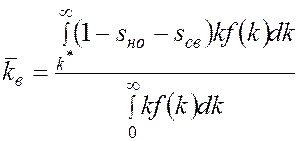 ; (3.8)
; (3.8)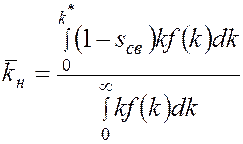 , (3.9)
, (3.9) — проницаемость обводнившегося слоя.
— проницаемость обводнившегося слоя. (3.10)
(3.10)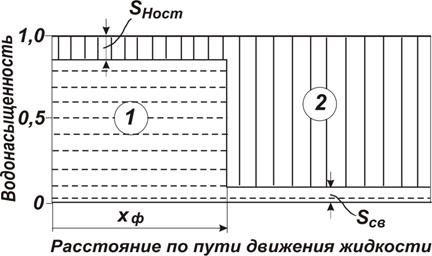
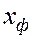 . Перед фронтом фильтруется только нефть, а позади — только вода.
. Перед фронтом фильтруется только нефть, а позади — только вода.
 , а затем обводненность медленно нарастает.
, а затем обводненность медленно нарастает. вещества плотностью
вещества плотностью  в элементе пласта (рис. 27) длиной
в элементе пласта (рис. 27) длиной  и шириной
и шириной 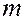 , составит
, составит (3.11)
(3.11)
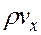 , вытесняется из элемента с массовой скоростью и
, вытесняется из элемента с массовой скоростью и  , а накопленный объем его
, а накопленный объем его  за время
за время  , получим с учетом того, что в элемент вошло больше вещества, чем из него вышло:
, получим с учетом того, что в элемент вошло больше вещества, чем из него вышло: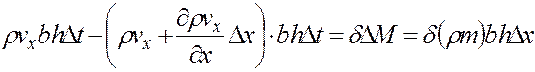 . (3.12)
. (3.12) (3.13)
(3.13)
 (3.14)
(3.14) (рис. 28). Рассматривая массовые скорости поступления вещества в куб и вытеснения из него, а также накопленный объем его в кубе, получим
(рис. 28). Рассматривая массовые скорости поступления вещества в куб и вытеснения из него, а также накопленный объем его в кубе, получим . (3.15)
. (3.15) . (3.16)
. (3.16) состоит из отнесенных к единице массы внутренней удельной энергии пород пласта и насыщающих его веществ
состоит из отнесенных к единице массы внутренней удельной энергии пород пласта и насыщающих его веществ  , удельной потенциальной
, удельной потенциальной 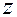 и кинетической энергии веществ, движущихся в пласте со скоростью
и кинетической энергии веществ, движущихся в пласте со скоростью  . Поэтому
. Поэтому . (3.17)
. (3.17)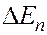 и произведенной удельной работы
и произведенной удельной работы  равно количеству подведенного к пласту тепла
равно количеству подведенного к пласту тепла  ,умноженного на механический эквивалент тепла
,умноженного на механический эквивалент тепла 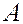 , т. е.
, т. е.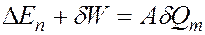 , (3.18)
, (3.18) . (3.19)
. (3.19) при отсутствии в нем химических или ядерных превращений вещества представляет собой тепловую энергию в единице массы пласта, так что
при отсутствии в нем химических или ядерных превращений вещества представляет собой тепловую энергию в единице массы пласта, так что , (3.20)
, (3.20)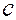 — удельная теплоемкость пласта; Т — температура. Положим, что пористый пласт насыщен водой. Тогда
— удельная теплоемкость пласта; Т — температура. Положим, что пористый пласт насыщен водой. Тогда  (
( - удельная теплоемкость пород пласта;
- удельная теплоемкость пород пласта;  - удельная теплоемкость воды,
- удельная теплоемкость воды,  = 1,046 кДж/(кг×К),
= 1,046 кДж/(кг×К),  = 4,184 кДж/(кг. К),
= 4,184 кДж/(кг. К),  ,
,  . Тогда
. Тогда  ,
,  =102×1,67×1=170 м. Удельная потенциальная энергия
=102×1,67×1=170 м. Удельная потенциальная энергия  ,
,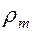 - плотность горных пород;
- плотность горных пород;  - плотность насыщающих пласт веществ, и умножать все виды удельной энергии, кроме внутренней, на
- плотность насыщающих пласт веществ, и умножать все виды удельной энергии, кроме внутренней, на  . При
. При  ,
, 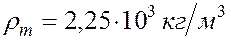 ,
, 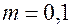
 .
.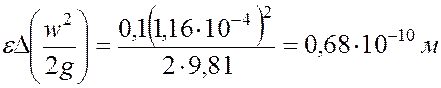 .
. получим 10 м. Изменение же температуры пласта всего на один градус равнозначно изменению удельной внутренней энергии почти на 200 м. Если разработка пласта ведется с использованием тепловых методов, то температура пласта может изменяться на сотни градусов и его удельная внутренняя энергия станет преобладающей среди других видов энергии. Оценим возможную величину работы, которую могут производить насыщающие пласт вещества. Удельную работу
получим 10 м. Изменение же температуры пласта всего на один градус равнозначно изменению удельной внутренней энергии почти на 200 м. Если разработка пласта ведется с использованием тепловых методов, то температура пласта может изменяться на сотни градусов и его удельная внутренняя энергия станет преобладающей среди других видов энергии. Оценим возможную величину работы, которую могут производить насыщающие пласт вещества. Удельную работу  ,. производимую насыщающим пласт веществом и отнесенную к единице массы вещества, определим следующим образом:
,. производимую насыщающим пласт веществом и отнесенную к единице массы вещества, определим следующим образом: , (3.21)
, (3.21)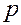 - давление;
- давление;  — объем вещества, насыщающего пласт в элементарном объеме пласта;
— объем вещества, насыщающего пласт в элементарном объеме пласта; 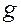 — ускорение свободного падения.
— ускорение свободного падения.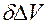 , характеризующая расширение вещества. При этом условно можно считать, что вещество, насыщающее пласт, расширяясь, как бы выходит за пределы элементарного объема пласта. Будем считать, что при бесконечно малом расширении вещества в элементарном объеме пласта масса вещества
, характеризующая расширение вещества. При этом условно можно считать, что вещество, насыщающее пласт, расширяясь, как бы выходит за пределы элементарного объема пласта. Будем считать, что при бесконечно малом расширении вещества в элементарном объеме пласта масса вещества  остается неизменной.
остается неизменной. и, следовательно,
и, следовательно, . (3.22)
. (3.22) . (3.23)
. (3.23) , где
, где  и
и  - давление и плотность газа при начальных условиях. Отсюда для идеального газа
- давление и плотность газа при начальных условиях. Отсюда для идеального газа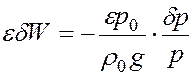 . (3.24)
. (3.24) ,
, 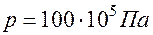 ,
,  ,
, 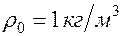 ,
, 

 . Тепловыделение в элементе пласта может происходить за счет экзотермических химических реакций и гидравлического трения и за счет теплопроводности. Уход тепла из элемента пласта за счет теплопроводности в дальнейшем будем учитывать при изменении внутренней энергии пласта
. Тепловыделение в элементе пласта может происходить за счет экзотермических химических реакций и гидравлического трения и за счет теплопроводности. Уход тепла из элемента пласта за счет теплопроводности в дальнейшем будем учитывать при изменении внутренней энергии пласта  (3.25)
(3.25) со скоростью
со скоростью  . Проницаемость пласта
. Проницаемость пласта  , пористость
, пористость 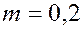 , плотность газа
, плотность газа  составляет 100 кг/м3. Тогда
составляет 100 кг/м3. Тогда .
. энергии. Это, конечно, незначительная величина. Однако, например, в призабойной зоне скважин скорость фильтрации того же газа может достигать
энергии. Это, конечно, незначительная величина. Однако, например, в призабойной зоне скважин скорость фильтрации того же газа может достигать  м/с, а иногда и более. Тогда при тех же остальных условиях, что и выше, значение
м/с, а иногда и более. Тогда при тех же остальных условиях, что и выше, значение 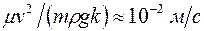 . В сутки из килограмма фильтрующегося в пласте газа выделится энергии почти 9кДж. Таким образом, можно заключить, что наиболее существенное изменение энергии в элементе пласта связано с переносом тепла за счет теплопроводности и конвекции. Определенный вклад в энергетический баланс пласта, особенно при высоких скоростях движения насыщающих его веществ, вносят работа расширения-сжатия веществ и гидравлическое трение.
. В сутки из килограмма фильтрующегося в пласте газа выделится энергии почти 9кДж. Таким образом, можно заключить, что наиболее существенное изменение энергии в элементе пласта связано с переносом тепла за счет теплопроводности и конвекции. Определенный вклад в энергетический баланс пласта, особенно при высоких скоростях движения насыщающих его веществ, вносят работа расширения-сжатия веществ и гидравлическое трение. и энергии сжатия
и энергии сжатия 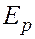 , а также считая, что тепло поступает в элементарный объем только за счет гидравлического трения, т. е. что
, а также считая, что тепло поступает в элементарный объем только за счет гидравлического трения, т. е. что  , получим
, получим (3.26)
(3.26)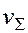 - вектор суммарной скорости теплопереноса в пласте за счет теплопроводности и конвекции,
- вектор суммарной скорости теплопереноса в пласте за счет теплопроводности и конвекции,  — вектор скорости фильтрации. Выражение (3.26) и есть дифференциальное уравнение сохранения энергии в пласте, выведенное при указанных выше предположениях.
— вектор скорости фильтрации. Выражение (3.26) и есть дифференциальное уравнение сохранения энергии в пласте, выведенное при указанных выше предположениях.


