
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Трифазна мережа, що живить кілька симетричних навантаженьСодержание книги
Поиск на нашем сайте
В розгалуженій мережі позначимо активні та реактивні потужності споживачів, відповідно, pk і qk, а потужності на ділянках мережі Pk і Qk . Складаємо їх послідовно для кожної ділянки, враховуючи навантаження (рис.7.5).
Рисунок 7.5. Схема розгалуженої мережі
Втрата напруги до найбільш віддаленої точки 4 визначається за допомогою формули (7.9) як сума втрат напруг на ділянках від джерела живлення до розглядуваної точки:
а поперечна складова
У формулах (7.13), (7.14)
Якщо позначити суму опорів ділянок від
Формули (7.15), (7.16) дозволяють обчислити і втрату напруги магістралі (рис. 7.6).
Рисунок 7.6. Магістраль, що живить декілька навантажень
Якщо магістраль однорідна і на всьому протязі має однакову площу перерізу, формулу (7.15) можна записати у вигляді
В останньому випадку втрата напруги визначається «моментом» навантаження. Якщо втрати напруги обчислюють, виходячи з потужності на ділянках лінії У ряді випадків при проектуванні мереж (наприклад, тих, що живлять зовнішнє освітлювальне навантаження міст і селищ) застосовують рівномірний розподіл навантаження по довжині лінії (рис. 7.7).
Рисунок 7.7. Лінія з рівномірно розподіленим навантаженням
Позначимо потужність на одиницю довжини лінії
При обчисленні втрати напруги навантаження, що рівномірно розподілене по всій довжині лінії, його можна замінити зосередженим, що прикладене до її середини. Приклад 7.1. Визначити найбільшу втрату напруги в кабельній мережі 6 кВ. Довжини й площі перерізу мідних жил кабелів вказані на рис.7.8. Індуктивний опір кабелів незалежно від перерізу можна прийняти X 0=0,08 Ом/км. Активні опори при площі перерізу жил кабелів 16; 35 та 95 мм² дорівнюють відповідно 1,15;0,52 та 0,2 Ом/км.
Рисунок 7.8. Розрахункова схема до прикладу 7.1
Втрата напруги до точки 4:
Втрата напруги до точки 3:
Найбільша втрата напруги Приклад 7.2. Лінія трифазного змінного струму напругою 10 кВ живить два навантаження (рис. 7.9). Уздовж всієї лінії підвішений сталевий багатожильний провід ПМС-50. Середньогеометрична відстань між проводами лінії
Рисунок 7.9. Розрахункова схема до прикладу 7.2
Для визначення активного і внутрішнього індуктивного опору сталевих проводів лінії необхідно знати струми на ділянках лінії:
Активні опори проводів на одиницю довжини:
Активні й індуктивні опори ділянок лінії:
Втрата напруги в лінії
Втрата активної потужності
Те ж у відсотках від потужності споживачів
Визначення площ перерізів проводів за допустимою втратою Напруги При виконанні розрахунків електричних мереж зустрічаються дві основні задачі. В першій задачі, що розглянута раніше, необхідно було перевірити втрати напруги від пункту живлення до точок приєднання приймачів електроенергії, знаючи навантаження мережі, а також всі її параметри. Така перевірка може знадобитись при складанні проекту, а також в умовах експлуатації. Друга задача – визначення площі перерізу проводів на ділянках мережі, з тим, щоб втрати напруги від пункту живлення до найбільш віддалених приймачів у режимі найбільших навантажень не перевищували допустимого значення Припустимо, що лінія живить одне трифазне симетричне навантаження. Як показано на рис. 7.4, б, втрата напруги в лінії складається з двох складових
Індуктивний опір лінії змінюється незначно зі зміною площі перерізу проводів. Тому в залежності від напруги лінії приймають середнє значення індуктивного опору.
Напруга лінії, кВ 110 35 6; 10 до 1 Середнє значення індуктивного опору
- повітряних 0,42 0,4 0,36 0,34 - кабельних – 0,12 0,08 0,07
Знаючи індуктивний опір
Допустима втрата напруги в лінії при передачі активної потужності
Згідно з умовою
визначимо шукану площу перерізу проводів лінії
Підбираємо найближче стандартне значення Розглянемо лінію, що живить декілька навантажень. Припустимо, що на протязі всієї лінії проводи мають однаковий переріз
При цьому спрощуються умови експлуатації. Постійна площа перерізу проводів застосовується, наприклад, в тих випадках, коли лінія прокладена у вигляді магістралі між двома пунктами живлення і може бути відімкнена з будь-якого її кінця, причому іноді ця лінія служить резервною перемичкою між пунктами живлення. Спочатку визначаємо допустиму втрату напруги при передачі тільки активної потужності
Шукану площу перерізу
звідки шукана площа перерізу
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 355; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.155.227 (0.011 с.) |


 (7.13)
(7.13) (7.14)
(7.14) ,
,  - модуль і фаза струму на розглядуваній ділянці мережі
- модуль і фаза струму на розглядуваній ділянці мережі ;
;  ;
; ,
,  - активний та індуктивний опори ділянок мережі.
- активний та індуктивний опори ділянок мережі. -го навантаження до джерела живлення
-го навантаження до джерела живлення  і
і  , то формули (7.13) і (7.14) можна перетворити до вигляду:
, то формули (7.13) і (7.14) можна перетворити до вигляду: ; (7.15)
; (7.15) . (7.16)
. (7.16)
 . (7.17)
. (7.17) і
і  , у формулу (7.13) необхідно підставляти опори цих же ділянок
, у формулу (7.13) необхідно підставляти опори цих же ділянок  та
та  і
і  , то у відповідності з формулою (7.15) треба застосовувати опори ліній
, то у відповідності з формулою (7.15) треба застосовувати опори ліній 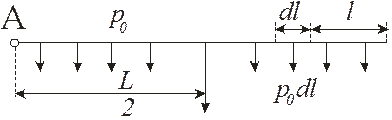
 . Втрата напруги в лінії з активним рівномірно розподіленим навантаженням
. Втрата напруги в лінії з активним рівномірно розподіленим навантаженням . (7.18)
. (7.18)


 =137 В.
=137 В. м. Визначити втрату напруги в лінії від пункту живлення до найбільш віддаленого споживача, знайти втрату активної потужності й виразити її у відсотках від потужностей споживачів.
м. Визначити втрату напруги в лінії від пункту живлення до найбільш віддаленого споживача, знайти втрату активної потужності й виразити її у відсотках від потужностей споживачів.
 А;
А; А.
А. Ом/км;
Ом/км;  Ом/км. Внутрішні індуктивні опори:
Ом/км. Внутрішні індуктивні опори:  Ом/км;
Ом/км;  Ом/км. Зовнішній індуктивний опір фази трифазної лінії на одиницю довжини
Ом/км. Зовнішній індуктивний опір фази трифазної лінії на одиницю довжини Ом/км.
Ом/км. Ом;
Ом; Ом;
Ом; Ом.
Ом.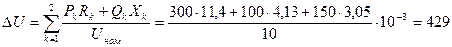 В.
В. кВт.
кВт. .
.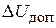 .
. та
та  (див. вирази (7.11) та (7.12)). Необхідно так підібрати площу перерізу проводів лінії, щоб втрата напруги не перевищувала допустимого значення.
(див. вирази (7.11) та (7.12)). Необхідно так підібрати площу перерізу проводів лінії, щоб втрата напруги не перевищувала допустимого значення. , Ом/км, для ліній:
, Ом/км, для ліній: . (7.19)
. (7.19) . (7.20)
. (7.20)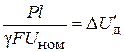
 . (7.21)
. (7.21) .
.
 (7.22)
(7.22) проводів лінії отримаємо, виходячи з умови живлення активних навантажень
проводів лінії отримаємо, виходячи з умови живлення активних навантажень ,
, . (7.23)
. (7.23)


