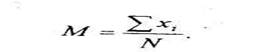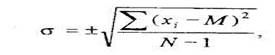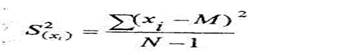Средние величины. Описательная статистика

Среднее. Среднее показывает "центральное положение" (центр) переменной и рассматривается совместно с доверительным интервалом. Обычно интерес представляют статистики (например, среднее), дающие информацию о популяции в целом. Чем больше размер выборки, тем более надежна оценка среднего. Чем больше изменчивость данных (больше разброс), тем оценка менее надежна.

Среднее арифм-кое (М) равно частному от деления суммы всех значений варьирующей величины (х1) на число единиц совокупности (N):

Конкретные значения варьирующего признака называются вариантами. Различают частоту вариантов, т.е. численность единиц совокупности, обладающих данным значением признака. Если частоты вариантов не равны между собой, то вычисляется средняя арифметическая взвешенная (средневзвешенная арифметическая):

гдеМ_у - средневзвешенная арифметическая;

ni - частоты вариантов;

N-сумма частот вариантов.

Для характеристики разброса значений принято пользоваться средним квадратичным отклонением (δ):

где ∑(хi - М)² - сумма отклонений каждого результата от среднего арифметического.

Знаменатель уменьшается на единицу, если число опытов небольшое (N ≤ 30), а при N>30 вычитание единицы не производится.

При вычислении среднего квадратичного отклонения среднего результата знаменатель подкоренного выражения будет N (N - 1).

Разброс анализируемой случайной величины по отношению к ее средней арифметической характеризуется дисперсией. Чем больше величина дисперсии, тем больше разброс величин, и наоборот, чем меньше дисперсия, тем теснее группируются около средней арифметической значения случайной величины.

Дисперсия и стандартное отклонение — наиболее часто используемые меры изменчивости переменной. Дисперсия меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости, когда значения переменной постоянны. Дисперсия S( x_i) вычисляется по формуле

При определении истинного значения среднего арифметического необходимо учитывать его ошибку. Для вычисления ошибки среднего арифметического пользуются формулой

где т - ошибка среднего арифметического;а - среднее квадратическое отклонение;N - число опытов.

Величина ошибки среднего арифметического указывает на те пределы, в которых может заключаться истинное значение среднего арифметического измеряемого показателя.

Относительная ошибка рассчитывается по формуле

Стандартное отклонение вычисляется как корень квадратный из дисперсии. Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего.

Минимум и максимум — это минимальное и максимальное значения переменной.

Медиана разбивает выборку на две равные части. Половина значений переменной лежит ниже медианы, половина — выше.

Медиана дает общее представление о том, где сосредоточены значения переменной, иными словами, где находится ее центр.

Квартили представляют собой значения, которые делят две половины выборки (разбитые медианой) еще раз пополам.

Таким образом, медиана и квартили делят диапазон значений переменной на четыре равные части.

Различают верхнюю квартиль, которая больше медианы и делит пополам верхнюю часть выборки (значения переменной больше медианы), и нижнюю квартиль, которая меньше медианы и делит пополам нижнюю часть выборки.

Мода представляет собой максимально часто встречающееся значение переменной. Мода - наиболее часто встречающаяся величина уровня качества - превышает среднее значение. Медиана разделила выборку на две равные части. Соотношение среднего значения, моды и медианы указывает на характер распределения исследуемого показателя и в совокупности позволяет оценить его асимметрию.Э ксцесс отрицательный, что характеризует кривую с более низкой и пологой вершиной. Но значение эксцесса велико, что свидетельствует о неоднородности реализуемой продукции по уровню качества.

Средствами MS Excel можно определить среднее значение (М), дисперсию (S2(xi)), стандартное отклонение (σ), доверительный интервал (m).

Указанные значения определяем следующим образом:

1 Вводим исходные данные в ячейки столбца (строки). Например, указанные выше значения кислотности хлеба введены в диапазон А2:А5.

2 Под столбцом (или строкой) исходных данных выделяем ячейку для результата оценки. Например, выделяем ячейку А6.

3 На панели нажимаем Вставка, затем - f_x Функция...

4 В окошке Мастер функций - шаг 1 из 2.Категория - выбираем Статистические.

Функция - выбираем СРЗНАЧ, нажимаем ОК.

5 В диалоговом окне СРЗНАЧ:

Число 1: щелкаем левой кнопкой мыши, а затем выделяем левой кнопкой мыши на диапазоне данных исследуемого ряда. В окошке Число 1 отразится диапазон исходных данных. Так, по приведенному примеру отразится диапазон А2:А5.

6 ОК. В выделенной под столбцом (строкой) ячейке отразится результат оценки (в примере в ячейке А6 будет цифра 2,87).

Аналогично с помощью Мастер функции рассчитываем ДИСП (дисперсию), СТАНДОТКЛОН (стандартное отклонение).

В экспериментальных исследованиях важно знать доверительный интервал значений показателей, т. е. интервал с обеих сторон от среднего значения выборки.

Указанное значение определяем следующим образом.

1 На панели нажимаем ВСТАВКА, затем - f_x Функция...

2 В окошке Мастер функций - шаг 1 из 2. Категория - выбираем Статистические. Функция - выбираем ДОВЕРИТ.

3 В диалоговом окне ДОВЕРИТ:

Альфа - вводим 0,5. Это уровень значимости, используемый для вычисления уровня надежности. Уровень надежности равняется 100*(1-α) процентам, или, другими словами, α = 0.05 означает 95 %-ный уровень надежности.

Стандартное _ откл — щелкаем левой кнопкой мыши в окошко, затем нажимаем левую кнопку мыши, указывая ячейку с известным значением стандартного отклонения (в нашем примере - это значение 0,45734).

Размер - указываем число значений в выборке (в примере число значений в выборке равно 4). ОК.

4 Результат запишется в выделенной ячейке (в примере результат равен 0,15).

Исходя из приведенного примера, среднее значение кислотности хлеба яичного с уровнем достоверности (надежности) 95 % находится в интервале 2,87 ± 0,15.

При необходимости проследить характер распределения и оценить меру разброса фактических величин вокруг среднего значения используется инструмент Описательная статистика, имеющийся в MS Excel. C помощью этого инструмента можно получить статистические характеристики вариационного ряда: среднее, стандартная ошибка, медиана, мода, стандартное отклонение, дисперсия, коэффициент эксцесса, коэффициент асимметрии, размах (интервал), максимальное значение, минимальное значение, сумма, число значений, k-е наибольшее и наименьшее (для любого заданного значения k) и уровень значимости (надежности) для среднего.