
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 2.2 С М О з обмеженою чергоюСодержание книги Поиск на нашем сайте
На станцію поточного ремонту автомашин надходить у середньому 1) година роботи ґаража коштує 34 грн; 2) за діагностику кожної машини, що ремонтується, беруть 20 грн; 3) година роботи кожного майстра з бригади з двох чоловік, що обслуговують ґараж, коштує 3,1 грн, простою – 1,1 грн; 4) податки складають 40% від заробленої суми; 5) інші витрати у середньому 20 грн з ґаража за добу. Визначити економічну доцільність уведення в експлуатацію ще одного ґаража, якщо його вартість 10000 грн. Прибуток станції знаходиться де Розв΄язок. 1. Знайдемо характеристики системи:
2.Знайдемо імовірності станів без черги:
Р0= (2,340/0! + 2,341/1! + 2,342/2! + 2,342/2!·((1,175-1,17)/(1,17-1)))-1=
Відносна пропускна спроможність Середній час роботи 2-х ґаражів:
Абсолютна пропускна спроможність, середнє число обслуговуваних машин: Імовірність зайнятості ґаража:
де середнє число зайнятих ґаражів –
Імовірність простою:
Ефективність роботи двох ґаражів:
=252грн/добу. ІІ. Визначимо економічну доцільність уведення в експлуатацію ще одного ґаража, коли працють три ґаража, 1. Характеристики системи ті ж самі, що і при
2. Знайдемо ймовірності станів без черги. Усі ґаражі не працюють: Р0= (2,340/0! + 2,341/1! + 2,342/2! +2,343/3! + 2,343/3!·((0,785-0,78)/(0,78-1)))-1= = Працює один ґараж:
Працюють два ґаражі:
Працюють три ґаражі:
Середній час роботи трьох ґаражів:
=24,18 год. Середнє число обслуговуваних машин:
Середнє число зайнятих ґаражів:
Імовірність зайнятості ґаража:
Імовірність простою ґаража:
Ефективність роботи трьох ґаражів:
=441,88 грн/добу. Економічна ефективність від уведення третього ґаража:
Термін окупності: Висновок: при даному режимі роботи обслуговується 8,352 машини за день, що приносить прибуток у розмірі 252 грн за один робочий день. При введенні третього ґаража число машин, що обслуговуються, збільшилося б до 10,14 машини, збільшився б також середній час роботи ґаражів - 24,18 час. Це, в свою чергу викликало б збільшення прибутків на 189,88 грн на день. Строк окупності 3-го ґаража склав 52,6 діб. Проект побудови 3-го ґаража ефективний. Необхідно прийняти рішення про будівництво. Задача 2.3 С М О із необмеженою чергою Фірма, що забезпечує зв'язком журналістів, які освітлюють міжнародну конференцію, має три лінії супутникового зв'язку. Потік заявок найпростіший зы щільністю 0,24 заявок/хв.. Середній час передачі повідомлення Журналіст зобов'язаний передати повідомлення якомога раніше у своє агентство або газету. Знайти прибуток фірми за добу (24 години), якщо хвилина розмови коштує у середньому 3,2 дол./хв, а за час чекання в черзі фірма сплачує клієнтові компенсацію 1,13 дол /хв. Визначити доцільність запровадження ще однієї лінії зв'язку, якщо її вартість 5000 дол, а конференція триває три дні. Прибуток фірми розраховується за формулою:
де сумарний час заняття каналів Розв΄язок. Початкові умови:
1) Характеристики системи: 2) 3) 4)
Імовірність відсутності повідомлень:
5) 6) 7) 8) Якщо число ліній зв’язку
Імовірність відсутності повідомлень:
+2,045/4!/(4-2,04))-1
=9088,68 дол.;
Висновок: при функціонуванні трьох ліній супутникового зв’язку фірма отримує прибуток у розмірі 7795,3 дол/добу. При введенні четвертої лінії зв’язку на час самміту (три доби) фірма отримає додатково 3880,14 $.Порівняно із витратами, необхідними для введення в експлуатацію четвертої лінії, це недостатньо. Тому проект невигідний. Якщо б самміт тривав би довше, то й додатковий прибуток був би вищим. За таких умов необхідно переглянути рішення про введення в експлуатацію четвертої лінії зв’язку. Задача 3.1 Розв΄язати аналітично та графічно гру, що задана матрицею платежів Розв΄язатигру, якщо платіжна матриця має вигляд
Розв΄язок Як прямуе із платіжної матриці, таблиця 13, виграші 1-го гравця
виграші 2-го гравця
Графічне розв΄язання гри для гравця А Для трьох стратегій гравця В знаходимо виграш
Таблиця 13 Платіжна матриця з цінами гри для вибраних стратегій гравців
Рис. 3.1– Графічне розв΄язання гри для гравця А
Виразимо
будуємо ці прямі Vi, і= 1; 2; 3, за двома точками на осях Х1 та V, рис. 3.1. Необхідні розрахунки проведені у таблиці 14. Відкидаємо ту пряму (стратегію), яка не проходить через точку оптимуму Якщо проходять усі три, то відкидаємо одну з двох, що мають однаковий нахил. Таблиця 14 Точки перетину прямих з осями
Висновок. Як випливає з рисунка 3.1, оптимальна змішана стратегія гравця А: зі імовірністю
Знайдемо графично оптимальну змішану стратегію гравця В. Імовірність застосування гравцем В відкинутої стратегії Розв'язуємо задачу графічно для двох стратегій
Висновок. Як випливає з рисунка 3.2, оптимальна змішана стратегія гравця В: зі ймовірністю
Таблиця 15 Точки перетину прямих з осями
Рис. 3.2 – Графічне розв΄язання гри для гравця В
Аналітичий розв΄язок задачі. Оскільки стратегія Таблиця 16 Спрощена платіжна матриця гри
Для гравця А:
Для гравця В:
Висновок. Імовірності застосування стратегій у оптимальній змішаній стратегії гравцем А: стратегія Імовірності застосування стратегій у оптимальній змішаній стратегії гравцем В: стратегія Такий вибір стратегій ґарантує гравцю А виграш, а гравцю в програш у 4 ПИТАННЯ ДО ІСПИТУ З НАВЧАЛЬНОЇ ДИСЦИПЛІНИ „ДОСЛІДЖЕННЯ ОПЕРАЦІЙ” 1. Динамічне програмування як наука управління економічними процесами. 2. Переваги та недоліки динамічного програмування. 3. Принцип Беллмана. 4. Розподіл капіталовкладень між підприємствами; постановка задачі, функціо- нальні рівняння. 5. Заміна обладнання: постановка задачі, функціональні рівняння. 6. Марківські процеси та їхні властивості. 7. Марківські ланцюги, матриця переходу. 8. Граф стану, імовірність стану системи після к-го кроку. 9. Різновиди і властивості стохастичних матриц. 10. Ланцюги Маркова, ергодична властивість, перехідний режим. 11. Рівняння Колмогорова для безперервного марковського процесу. 12. Теорема Маркова для безперервних марковських ланцюгів. 13. Простіший потік подій та його властивості. 14. Задачі й предмет теорії масового обслуговування. Характеристики ефектив- ності обслуговування. 15. Класифікація систем масового обслуговування (С.М.О.) та їх основні харак- теристики. 16. Рівняння Ерланга, формули Ерланга, приклад. 17. С М О. із очікуванням, імовірності подій та інші характеристики системи, приклад. 18. С М О із необмеженою чергою імовірності станів, інші характеристики, приклад. 19. Теорія ігор, визначення гри, види моделей. 20. Антагоністична гра у нормальній формі, принцип гарантованого результату. 21. Рівновага у грі, чисті та змішані стратегії. 22. Стійкість отриманих розв΄язків,теорема про мінімакс. 23. Спрощення гри, способи пошуку оптимальних стратегій. 24. Розв΄язокгри 2·2; графічно, аналітично. 25. Алгоритми гри 2·n, m·2. 26. Розв΄язокгри m·n за допомогою систем лінійних рівнянь. 27. Поняття про статистичні ігри. 28. Вибір оптимальної стратегії статиста. 29. Критерій Вальда. 30. Критерій Севіджа.
СПИСОК ЛІТЕРАТУРИ
Основна 1. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое програмпрограммирование. – М.: Высшая школа, 1986.– 429 с. 2. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986. – 341 с. 3. Вентцель Е.С. Исследование операций. – М.: Сов. радио, 1972. – 407 с. 4. Заиченко Ю.П., Шумилова С.А. Исследование операций: сборник задач. – К.: Вища школа, 1990. – 367 с. 5. Кузнецов А.В., Новикова Г.И., Холод Н.И. Сборник задач по математическо- му программированию. – Минск: Вышейшая школа, 1985. – 462 с. 6. Сакович В.А. Исследование операций (детерминированные методы и модели). – Минск: Вышейшая школа, 1984. – 398 с. 7. Вентцель Е.С. Теория вероятностей: Учебник для вузов. – 5-е изд. стер. – М.: Высшая школа, 1985. – 513 с. 8. Ивченко Г.И., Каштанов В.А., Коваленко И.Н. Теория массового обслужива- ния. – М.: Высшая школа, 1982. – 359 с.
Додаткова 9. Вентцель Е.С., Овчаров Л.А., Теория вероятностей. – М.: Наука,1973. – 368 с. 10. Черніченко В.Є., Юхименко М.Ю. Методичні рекомендації щодо самостійної роботи з вивчення навчальної дисципліни “Дослідження операцій” для студентів денної та заочної форм навчання зі спеціальностей: 7.050107 – “Економіка підприємств”, 7.050201 – “Менеджмент організацій”– Кременчук: КДПУ, 2000. – 25 с. 11.Черніченко В.Є., Юхименко М.Ю. Методичні вказівки щодо виконання розрахунково-графічних робіт з курсу «Дослідження операцій та методи оптимізації» за темою «Розв'язання конфліктних ситуацій в економіці методами теорії ігор» для студентів денної та заочної форм навчання зі спеціальностей: 7.050107, 7.050107 с – «Економіка підприємства», 7.050201 – «Менеджмент організацій».– Кременчук: КДПУ, 2000. – 40 с. 12.Черніченко В.Є., Юхименко М.Ю. Методичні вказівки щодо виконання розрахунково-графічних робіт з курсу «Дослідження операцій та методи оптимізації» за темою «Випадкові марковські процеси та системи масового обслуговування» для студентів денної та заочної форм навчання зі спеціальностей: 7.050107, 7.050107 с – «Економіка підприємства», 7.050201– «Менеджмент організацій».– Кременчук: КДПУ, 2000. – 57 с.
Додаток А Зразок оформлення титульної сторінки контрольної роботи
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ КРЕМЕНЧУЦЬКИЙ ДЕРЖАВНИЙ ПОЛІТЕХНІЧНИЙ УНІВЕРСИТЕТ ІМЕНІ МИХАЙЛА ОСТРОГРАДСЬКОГО
кафедра ЕКОНОМІКИ ШИФР (НОМЕР ЗАЛІКОВОЇ КНИЖКИ)
КОНТРОЛЬНА РОБОТА З навчальної ДИСЦИПЛІНИ “ДОСЛІДЖЕННЯ ОПЕРАЦІЙ”
СтудентА (ки) групи________ Факультету УПРАВЛІННЯ Прізвище, ім'я, ПО БАТЬКОВІ П І Б ВИКЛАДАЧА
Кременчук 200_ Методичні вказівки щодо виконання контрольної роботи з навчальної дисципліни „Дослідження операцій” для студентів заочної форми навчання з напряму 6.030601– „Менеджмент”
Укладач к.т.н., доц. В.Є. Черніченко Відповідальний за випуск зав. кафедри економіки О.І. Маслак
Підп. до друкуФормат 60*841/16. Папір тип. Друк ризографія. Ум. друк.арк.______Наклад прим. Зам. №. Безкоштовно.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.231.116 (0.008 с.) |

 маш/год, потік заявок найпростіший. Є два ґаражі для ремонту. На подвірї станції можуть знаходитися одночасно ≤
маш/год, потік заявок найпростіший. Є два ґаражі для ремонту. На подвірї станції можуть знаходитися одночасно ≤  машини, що очікують черги. Середній час ремонту однієї машини – tоб.=2,6 год. Визначити прибуток роботи станції за добу (12 годин), якщо:
машини, що очікують черги. Середній час ремонту однієї машини – tоб.=2,6 год. Визначити прибуток роботи станції за добу (12 годин), якщо: ,
,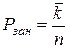 ;
;  ;
;  ;
;  ;
;  ;
; 
 ;
;  ;
; 
 –тривалість робочого дня.
–тривалість робочого дня.


 =(1+2,34+2,74+2,74·((2,192-1,17)/0,17))-1=22,56-1=0,044.
=(1+2,34+2,74+2,74·((2,192-1,17)/0,17))-1=22,56-1=0,044. ;
; ;
; .
. .
.
 .
. ,
, ґаражів,
ґаражів, .
. .
.

 .
. :
: ,
, 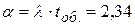 , окремо
, окремо 
 .
. .
. .
. .
.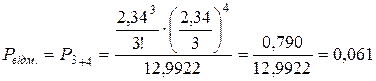 ;
; ,
,  .
.
 .
. .
. .
.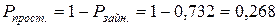 .
.


 хв /заявок, випадкова величина, що має показовий розподіл.
хв /заявок, випадкова величина, що має показовий розподіл. дол,
дол, , число заявок за добу
, число заявок за добу  , сумарний час очікування
, сумарний час очікування  , доцільність запровадження ще однієї лінії зв'язку
, доцільність запровадження ще однієї лінії зв'язку  , де П4 - прибуток за добу при n=4.
, де П4 - прибуток за добу при n=4. заявок/хв;
заявок/хв;  – вартість одної хвилини розмови;
– вартість одної хвилини розмови;  – компенсація.
– компенсація.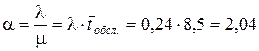 – середнє число заявок.
– середнє число заявок. – черга не накопичується, система стала.
– черга не накопичується, система стала. – середнє число зайнятих каналів.
– середнє число зайнятих каналів. ,
,  , число заявок, що обслуговуються за добу:
, число заявок, що обслуговуються за добу:

 .
. хвилин очікує один клієнт.
хвилин очікує один клієнт. (хвилин) – час очікування за добу всіх клієнтів.
(хвилин) – час очікування за добу всіх клієнтів. - час обслуговування всіх клієнтів за добу.
- час обслуговування всіх клієнтів за добу. $ - прибуток фірми при трьох лініях зв’язку.
$ - прибуток фірми при трьох лініях зв’язку. :
: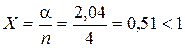 – черга не накопичується – стан сталий;
– черга не накопичується – стан сталий; (2,040/0!+ 2,041/1!+2,042/2!+2,043/3!+2,044/4!+
(2,040/0!+ 2,041/1!+2,042/2!+2,043/3!+2,044/4!+ ;
;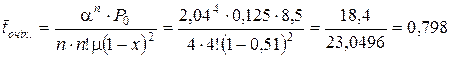 хвилин;
хвилин;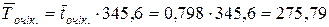 ;
; ;
;
 .
.
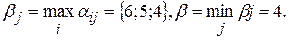
 - немає сідлової точки, рішення шукаємо серед змішаних стратегій.
- немає сідлової точки, рішення шукаємо серед змішаних стратегій. гравця А при застосуванні гравцем А змішаної стратегії
гравця А при застосуванні гравцем А змішаної стратегії  , де
, де  - ймовірність застосування стратегії
- ймовірність застосування стратегії  , і=1;2.
, і=1;2.









 через
через  . Імовірність повної групи подій
. Імовірність повної групи подій 
 :
: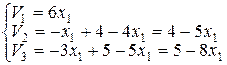 ,
, . Це пряма
. Це пряма  , яка відповідає стратегії гравця В,
, яка відповідає стратегії гравця В,  .
.

 застосовувати стратегію
застосовувати стратегію  ,а потімзі імовірністю
,а потімзі імовірністю застосовувати стратегію
застосовувати стратегію 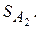 У результаті застосування оптимальної змішаної стратегії гравцем А його виграш складає
У результаті застосування оптимальної змішаної стратегії гравцем А його виграш складає  грош. один.
грош. один. . Для гравця В залишилося 2 стратегії. Для двох стратегій гравця А знаходимо програш
. Для гравця В залишилося 2 стратегії. Для двох стратегій гравця А знаходимо програш  гравця В при застосуванні гравцем В змішаної стратегії
гравця В при застосуванні гравцем В змішаної стратегії  , де
, де  – ймовірність застосування стратегії
– ймовірність застосування стратегії  ,
,  .
. 
 Будуємо ці прямі W1,W3 за двома точками на осях У1 та V. Необхідні розрахунки проведені у таблиці 15.
Будуємо ці прямі W1,W3 за двома точками на осях У1 та V. Необхідні розрахунки проведені у таблиці 15. застосовувати стратегію
застосовувати стратегію 
 застосовувати стратегію
застосовувати стратегію  У результаті застосування оптимальної змішаної стратегії гравцем В його програш складає
У результаті застосування оптимальної змішаної стратегії гравцем В його програш складає  для гравця В не буде використовуватись, тобто ймовірність її застосування
для гравця В не буде використовуватись, тобто ймовірність її застосування  ;
; ;
; .
. ;
; .
. ; стратегія
; стратегія  .
. ; стратегія
; стратегія  ; стратегія
; стратегія  .
.


