Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие сведения по квантовой механикеСодержание книги
Поиск на нашем сайте
ВВЕДЕНИЕ
Электроникой называется область науки и техники, занимающаяся разработками и исследованиями электронных приборов и устройств, построенных с использованием этих приборов, в том числе интегральных микросхем.
Электронными приборами называются приборы, действие которых основано на управлении движением электронов в различных средах с помощью электрических и магнитных полей. К ним относятся электровакуумные, газоразрядные и полупроводниковые приборы. В электровакуумных приборах электроны движутся в высоковакуумном промежутке, между электродами прибора. В газоразрядных приборах электроны перемещаются в газе, находящемся при таком давлении, при котором велика вероятность столкновения электронов с молекулами газа и их ионизация. Следовательно, на процессы в таких приборах будет влиять движение ионов. В полупроводниковых приборах электронв движутся внутри кристаллической решетки полупроводника и управляются полями, созданными внутри полупроводника. В абсолютном большинстве (более 90%) случаев устройства современной электроники изготовляются с использованием полупроводниковых приборов. Использование полупроводников в электронике прошло длительный путь – от первого детектора на кристалле сернистого свинца до современных интегральных микросхем. Начало бурного развития полупроводниковой электроникисвязано с созданием биполярного транзистора. Уравнение Шредингера
Мы уже разобрались, что состояние микрочастицы не может быть охарактеризовано совокупностью координат и проекцией импульса, как в классической механике. Так что же тогда отражает состояние микрочастицы? Шредингер предположил, что существует некоторая функция координат пространства и времени
где
m – масса покоя микрочастицы; Ñ2 - оператор Лапласа;
W(x,y,z,t) – потенциальная энергия микрочастицы во внешнем силовом поле; если микрочастица свободна, то W(x,y,z,t)=0. Отметим особенности уравнения Шредингера: 1. Это уравнение – дифференциальное уравнение частных производных, хорошо известное как волновое уравнение; его решением являются функции, описывающие процесс распространения волн в пространстве.
2. Уравнению () могут удовлетворять только комплексные значения. Поскольку комплексные числа – это математическая абстракция, не имеющая физического смысла, то и волновая функция y тожже не имеет физического смысла и значит, сама по себе не характеризует состояние микрочастицы. Но оказывается, что физический смысл имеет произведение волновой функции y и комплексно сопряженной с ней функции y y*= Физический смысл произведения yy* заключается в следующем: Это произведение есть действительная функция, численное значение которой для данной точки пространства в данный момент времени, равно вероятности нахождения микрочастицы в единичном пространстве окружающем данную точку. Эту вероятность обозначают W(x,y,z,t).
или сокращенно
В соответствии с таким физическим смыслом волновая функция должна быть непрерывной и иметь непрерывную первую производную, однозначной и конечной во всех точках пространства, т.к. вероятность нахождения микрочастицы не может быть величиной неоднозначной, бесконечной или скачкообразно изменяться от точки к точке. Отметим, что если мы рассматриваем поведение не одной, а совокупности (или системы) микрочастиц, то оно описывается их общей волновой функцией, зависящей от координат всех частиц. Например, для ситстемы из двух микрочастиц волновая функция имеет вид:
где x1, y1, z1 – координаты первой микрочастицы; x2, y2, z2 - координаты второй микрочастицы. Произведение Потенциальная энергия, входящая в уравнение Шредингера, является в общем случае функцией координат и времени. Однако во многих практически важных задачах потенциальная энергия является функцией только координат и не зависит от времени. Для таких задач волновую функцию можно представить в виде:
где Е – полная энергия микрочастицы. Функция
которое называется амплитудным уравнением Шредингера. Силовое поле, в котором потенциальная энергия микрочастицы не зависит от времени, называется стационарным. Состояния микрочастиц в стационарном поле называются стационарными состояниями. Т.е. амплитудное уравнение Шредингера описывает стационарные уравнения микрочастиц. Каждое состояние микрочастицы описывается одной волновой функцией. Если уравнение Шредингера допускает решение в виде нескольких волновых функций, то это означает, что микрочастица может находиться в нескольких различных состояниях.
Полупроводники
Твердые материалы условно делятся на проводники, полупроводники и диэлектрики. Это разделение связано с количеством (концентрацией) свободных носителей заряда в материале. Свободный носитель заряда – это носитель заряда, способный свободно передвигаться в кристаллической решетке материала. Чем больше этих свободных носителей, тем больше проводимость материала. В проводниках с.н. очень много и его проводимость велика (сопротивление мало) В диэлектриках – практически нет, сопротивление ОЧЕНЬ велико. ПП занимает промежуточное положение как по кол-ву с.н., так и по проводимости. Уровень Ферми
Вероятность нахождения электрона на том или ином энергетическом уровне при температуре Т определяется функцией Ферми – Дирака:
где WF – энергетический уровень, называемый уровнем Ферми. При Т=0°К вероятность занятия электронами уровней W > WF равна нулю:
а уровней W < WF единице:
При Т=0°К фуекция fn(W) имеет ступенчатый характер. Вероятность занятия электронами уровней в ЗП = 0, а в ВЗ = 1. При Т > 0°К появляется небольшая вероятность занятия электронами уровней в ЗП, а вероятность занятия уровней в ВЗ соответственно снижается. Из формулы Ферми – Дирака видно, что при температуре, отличной от абсолютного нуля (Т>0), уровень Ферми – это такой энергетический уровень W = WF, формальная вероятность заполнения которого электроном равна 0,5 (т.к. е° = 1). Формальное потому, что уровень Ферми находится в запрещенной зоне и фактически не может быть занят электроном. Таким образом, конкретный смысл имеют только те участники кривой распределения fn(W), которые расположены в ЗП и в ВЗ. Кривая распределения Ферми – Дирака всегда симметрична относительно уровня Ферми. Из этого, в частности, следует, что в собственном полупроводнике уровень Ферми расположен посередине ЗЗ. При повышении температуры от нуля появляется определенная вероятность занятия электронами энергетических уровней в ЗП. Но при этом на такую же величину снижается вероятность нахождения электронов в ВЗ. Нетрудно видеть, что при симметричном размещении кривой распределения fn(W) относительно уровня Ферми это возможно только в случае, если уровень Ферми будет находиться посередине ЗЗ.
Беспримесный полупроводник.
В химически чистом полупроводнике, например Ge, при Т=0°К электронов в ЗП нет. Все валентные электроны локализованы вблизи атомов и попарно образуют ковалентные связи между соседними атомами. Все энергетические уровни в ЗЗ заняты. Валентные электроны совершают хаотические туннельные переходы из одной потенциальной ямы в другую, но в любой момент времени все энергетические состояния остаются заполненными. Время перехода t~10-15 сек насколько мало, что неопределенность энергии электрона, совершающего туннельный переход, в соответствии с принципом неопределенности ∆Е ×∆t ³ h, составляет несколько эВ. Зонная диаграмма для беспримесного полупроводника изображена на рис.1. Примеси в полупроводниках.
На процесс образования свободных электронов и дырок в полупроводнике большое влияние оказывают нарушения правильной структуры кристаллической решетки, а также наличие примесей. Атомы примесей обычно замещают в узлах решетки атомы основного вещества, образуя дефекты замещения. Примесные атомы могут попасть так же в междоузлия и образовать дефекты внедрения. В полупроводники, используемые для изготовления полупроводниковых приборов, предварительно очищенные от случайных примесей, вводят специальные примеси, обеспечивающие преимущественную концентрацию либо свободных электронов, либо дырок. Для получения преимущественной концентрации электронов в качестве примесей используются вещества с валентностью, превосходящей валентность основного полупроводника. Такие примеси называются донорными. Так, для Ge и Si, валентность которых S=4, в качестве донорных примесей используются пятивалентные P или As. Преимущественная концентрация дырок получается за счет примесей с меньшей валентностью – акцепторных примесей. Такими примесями могут служить трехвалентные бор, Al, In и т.д. Электронный полупроводник (n-типа)
Из пространственно – энергетической диаграммы (рис.5,б) видно, что периодическая j-ая функция вблизи атома примеси искажается и пятый валентный электрон, а значит, и атом примеси занимают отдельный локальный энергетический уровень в ЗЗ вблизи дна ЗП. Такое расположение в ЗЗ пятого электрона возможно, потому что он не является свободным электроном, а находится в j-ой яме вблизи своего атома. Естественно, что для отделения этого электрона от атома – перевода его в ЗП – требуется значительно меньше энергии, нежели для перемещения любого валентного электрона из ВЗ в ЗП ∆Eg < ∆Eз. Энергия ∆Ед , требуемая для этого, называется энергией ионизации. При ионизации атома донорной примеси, называемого донором, в зоне проводимости появляется свободный электрон, а сам атом примеси превращается в положительно заряженный ион. В отличие от процесса перехода валентности электрона из валентной зоны в зону проводимости при генерации пар зарядов здесь не появляется дырка, т.к все валентные связи вблизи донорного атома замещены. Таким образом, положительный ион примеси в отличие от дырки – заряд неподвижный, и, следовательно, в процессе ионизации доноров образуются подвижные заряды лишь одного знака – свободные электроны. Обычно концентрация атомов примеси в полупроводниках составляет 10-6: 10-3 %. Поэтому атомы примеси отстоят друг от друга на расстояния, измеряемые, по меньшей мере, сотнями периодов решётки. Волновые ф-ции этих атомов можно считать неперекрывающимися, а их энергетический уровень не расщепляется в энергетическую зону, а образует единый для всех атомов локальный энергитический уровень, располагающийся на зонной диаграмме вблизи дна зоны проводимости (рис.5,в). Вывод: В полупроводниках с донорными примесями при Т>0°К образуется преимущественная концентрация электронов. Такие полупроводники называются электронными полупроводниками или n-полупроводниками. Дырочный полупроводник (р-типа).
В случае добавления в полупроводник акцепторной примеси одна из валентных связей вблизи атома- акцептора остаётся незаполненной (рис.6,а).
Рис. 6,а. Примесной атом In в кристалле Ge.
Такое состояние нельзя назвать дыркой, т.к. атом акцептора электрически нейтрален. Потенциальная функция вблизи атомов примеси искажается (рис.6,б).
Рис. 6,б. Положение примесного атома In на потенциальной диаграмме.
У края потенциальной ямы акцептора энергитический уровень, лежащий несколько выше потолка валентной зоны, остаётся незаполненным. В результате теплового возбуждения один из валентных электронов соседних атомов может нарушать валентную связь и заместить свободный энергитический уровень (заполнить валентную связь) вблизи атома акцептора. При этом четвёртый электрон связан с акцептором лишь квантомеханическими силами, т.е. его энергетическое состояние окажется выше энергии остальных трёх электронов на величину, примерно равную классической кулоновской энергии. В результате такого перехода вблизи соседнего атома, которому ранее принадлежал рассмотренный электрон, образуется дырка, а атом акцептора превратится в неподвижный отрицательно заряженный ион. Следовательно, в процессе ионизации акцепторов образуется преимущественная концентрация дырок – образуются подвижные носители лишь одного знака. Такие полупроводники называются дырочными или р-полупроводниками. Как и в случае донорных примесей, положение акцепторов в зонной диаграмме характеризуется единым локальным энергетическим уровнем, расположенным вблизи потолка валентной зоны (рис.6,в).
Выводы: В полупроводнике, в отличие от металлического проводника, ток образуется не только за счет направленного движения (дрейфа) отрицательно заряженных свободных электронов, но и за счет дрейфа положительно заряженных дырок.
Типы рекомбинации В зависимости от механизма различают три вида рекомбинации: межзонную рекомбинацию, рекомбинацию через локальные центры и поверхностную рекомбинацию. Межзонная рекомбинация осуществляется при переходе свободного электрона из зоны проводимости в валентную зону, что сопровождается уничтожением свободного электрона и дырки, на месте которой появляется связанный электрон. Этот процесс совершается при соблюдении законов сохранения энергии и импульса. Так как энергия электрона в валентной зоне меньше энергии электрона в зоне проводимости, то процесс межзонной рекомбинации должен сопровождаться выделением энергии ΔE ≈ Eпр – EB (49) В зависимости от того, на что расходуется энергия, различают следующие виды межзонной рекомбинации: Излучательную, при которой энергия ΔЕ излучается в виде кванта света (фотона); безизлучательную, при которой энергия ΔЕ передается кристаллической решетке, то есть расходуется на образование фононов. При излучательной межзонной рекомбинации в соответствии с законом сохранения энергии должен испускаться фотон с энергией hυ ≈ Eпр – EB (50) Вместе с тем из закона сохранения импульса следует, что hυ/С = Pпр –PB (51) Поскольку импульс фотона hυ/С ничтожно мал по сравнению с импульсом электрона, то последнее равенство можно переписать так Pпр –PB ≈ 0 (52) Рассматривая – PB как импульс свободной дырки, приходим к выводу, что при межзонной излучательной рекомбинации возможны лишь такие переходы, при которох электрон зоны проводимости встречается с дыркой валентной зоны, имеющей равный по величине и противоположный по направлению импульс. Несложно показать, что скорость межзонной излучательной рекомбинации увеличивается по мере уменьшения ширины запрещенной зоны полупроводника и увеличение его температуры. Поэтому данный вид рекомбинации может иметь единственное значение лишь для полупроводников с узкой запрещенной зоной и при достаточно высоких температурах.
Опыт, однако, показывает, что с увеличением ширины запрещенной зоны безизлучательная рекомбинация все более преобладает над излучательной. Это противоречие объясняется тем, что по мере увеличения ширины запрещенной зоны более вероятными становятся не прямые переходы через нее, а переходы через локальные уровни, расположенные в запрещенной зоне. Рекомбинация через локальные уровни (центры). Как мы выяснили раньше, наличие дефектов и примесей в полупроводнике приводит к появлению в его энергетической диаграмме локальных энергетических уровней, расположенных в запрещенной зоне. Рассмотрим, какую роль они играют в процессе рекомбинации свободных носителей зарядов. Пусть в запрещенной зоне донорного полупроводника, имеющего значительную концентрацию электронов зоны проводимости, располагается свободный локальный уровень Ел (рис. 8а), наличие которого обусловлено присутствием примесного атома или дефекта решетки. В этом случае рекомбинация проходит в два этапа. Первым этапом является захват электрона зоны проводимости указанным примесным атомом ёёёёёё (или, как горят, захват электрона проводимости локальным уровнем Ел, как показано стрелкой 1 на рис. 8а). Дальнейшее поведении захваченного электрона может быть двояким. Электрон может перейти в валентную зону (стрелка 2) на свободный уровень, что эквивалентно захвату на локальный уровень дырки и ее рекомбинации с электроном. Возможен и показанный стрелкой 3 обратный тепловой переброс электрона в зону проводимости. Этомт процесс препятствует рекомбинации электрона и дырки. Таким образом, интенсивность процесса рекомбинации определяется соотношением вероятностей процессов, указанных стрелками 2 и 3. Если локальные уровни располагаются близко к дну зоны проводимости или к потолку валентной зоны (рис. 8б), то есть являются мелкими, то вероятность протекания через них рекомбинации так же мала, как и вероятность межзонной рекомбинации. Поэтому наличие мелких локальных уровней приводит лишь к энергичному обмену электронами между ними и зоной проводимости (или валентной зоной) и не дает вклада в процесс рекомбинации. Дефекты или примеси, приводящие к появлению таких локальных уровней, называют ловушками захвата или центрами прилипания. Если же локальный уровень глубокий, то вероятность обратного переброса (например, электрона в зону проводимости) незначительна, преобладает процесс захвата дырки, то есть происходит интенсивный процесс рекомбинации. Дефекты или примеси, приводящие к появлению глубоких локальных уровней, на которых протекает процесс рекомбинации свободных электронов и дырок, называют рекомбинационными ловушками или центрами рекомбинации. Высокая интенсивность процесса рекомбинации на рекомбинационных ловушках объясняется тем, что при этом механизме избыточная энергия передается кристаллической решетке в два этапа (двумя примерно равными порциями), то есть на каждом этапе в реакции участвует меньшее число фононов, чем при межзонной рекомбинации. Немаловажное значение имеет также тот факт, что вероятность встречи дырки с неподвижным электроном, локализованным на дефекте, значительно выше вероятности встречи её с подвижным электроном. У примесных акцепторных полупроводников, имеющих значительную концентрацию дырок в валентной зоне, первым этапом рекомбинации является переход дырки из валентной зоны на локальный рекомбинационный уровень, а вторым этапом – захват электрона зоны проводимости и его рекомбинация с дыркой. Обратный тепловой переброс дырки в валентную зону препятствует процессу рекомбинации. Отметим, что интенсивность протекания рекомбинации через рекомбинационные ловушки зависит от степени легирования полупроводника. В собственном полупроводнике она минимальна и увеличивается как по мере добавления донорных, так и по мере добавления акцепторных примесей.
Свойства р-n-перехода.
Рассмотрим процессы, происходящие в плоскостном симметричном р-n-переходе.
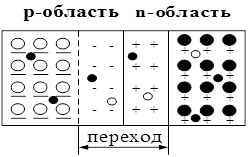
Р-n-переход без внешнего напряжения. В момент образования р-n-перехода как р-область, так и n-область электрически нейтральны. Но в р-области много дырок и мало свободных электронов, а в n-области наоборот, много свободных электронов и мало дырок. Резкое различие концентраций одноименных носителей заряда в р- и n-областях приводит к возникновению диффузии. Дырки, совершающие хаотическое тепловое движение в р-области, начнут переходить в n-область. В обратном направлении будут перемещаться свободные электроны. Таким образом, через границу раздела областей начнет протекать ток диффузии, образованный основными носителями заряда и содержащий дырочную и электронную составляющие: Iдиф = Iр диф + In диф Поскольку за направление тока принято направление перемещения положительных зарядов, ток диффузии будет протекать от р-области к n-области. В результате диффузии нарушается электрическая нейтральность р- и n-областей. В р-области вблизи границы раздела областей выступят нескомпенсированные отрицательные заряды атомов акцепторной примеси т.к. часть ранее компенсировавших их положительно заряженных дырок перейдет в n-область, а другая часть рекомбинирует с пришедшими из n-области свободными электронами. В приконтактной части n-области появятся нескомпенсированные положительные заряды атомов донорной примеси, поскольку компенсировавшие их ранее отрицательно заряженные свободные электроны частично перейдут в p-область, а частично рекомбинируют с диффундирующими n-области дырками. Таким образом, по обе стороны от границы раздела областей появятся заряды противоположных знаков (рис.2а). Энергетическая диаграмма, т.е. энергия, которой будет обладать электрон, находясь в той или иной обаласти, изображена на рис.2б. Между ними образуется электрическое поле, препятствующее диффузионному перемещению основных носителей заряда и называемое поэтому потенциальным барьером. Приконтактные участки p- и n-областей с появившимися нескомпенсированными зарядами атомов акцепторной и донорной примесей являются p-n-переходом. По мере перехода основных носителей заряда через границу раздела и роста в результате этого потенциального барьера, ток диффузии будет уменьшаться, так как все меньшее число основных носителей заряда будет иметь энергию, достаточную для преодоления потенциального барьера.
Высота потенциального барьера равна контактной разности потенциалов и обычно составляет десятые доли вольта. Чем больше концентрация примесей, тем выше концентрация основных носителей, и тем большее число их диффундирует чрез границу.
С возникновением электрического поля на границе раздела областей появляется возможность обратного перехода носителей заряда: дырок из n-области в p-область и свободных электронов из p-области в n-область. Так, дырка, совершающая тепловое хаотическое движение в n-области вблизи перехода, может попасть в электрическое поле перехода, которое для нее в данном случае (при переходе из n-области в p-область) не является потенциальным барьером, а, наоборот, является ускоряющим. Поэтому дырка будет переброшена полем в p-область. При этом в p-области будет скомпенсирован отрицательный заряд одного из атомов акцепторной примеси, расположенного вблизи границы раздела областей. В то же время свободный электрон, совершающий хаотическое тепловое движение в p-области, попав в поле перехода, будет переброшен им в n-область, где скомпенсирует один из положительных атомов донорной примеси. Переходя через границу раздела областей, неосновные носители заряда образуют дрейфовый ток, состоящий, как и ток диффузии, из дырочной и электронной составляющих:
Дрейфовый ток препятствует повышению потенциального барьера и понижению диффузионного тока до нуля. В установившемся режиме в p-n-переходе наступает динамическое равновесие: ток диффузии, понижаясь, становится равным встречному дрейфовому току и результирующий ток через переход становится равным нулю. Величина дрейфового тока определяется концентрацией неосновных носителей заряда в p-n-областях (чем больше неосновных носителей в данной области, тем больше вероятность попадания их в поле перехода) и практически не зависит от напряженности электрического поля перехода. Поскольку концентрация не основных носителей заряда в р- и n- областях, а значит и дрейфовый ток, в сильной мере зависит от температуры, дрейфовый ток через р-n-переход принято называть тепловым током. Диффузия основных носителей заряда в смежную область при образовании р-n-перехода и усиленная рекомбинация их там приводят к тому, что внутри р-n-перехода остается очень мало носителей заряда, то есть р-n-переход представляет собой ток называемый обедненный слой. Однако сопротивление р-n-перехода не определяется сопротивлением обедненного слоя, т.к. токи, протекающие через р-n-переход, образуются в основном носителями заряда р- и n-областей, а не обедненного слоя. Основными величинами, характеризующими р-n-переход в равновесном состоянии, являются высота потенциального барьера, называемая также контактной разностью потенциалов, Δφ0 или UK и ширина перехода l0.
Мкость р-n-перехода Инжекция неосновных носителей заряда в случае приложения к р-n-переходу прямого напряжения и экстракция неосновных носителей заряда в случае приложения к переходу обратного напряжения приводят к изменению по сравнению с равновесными концентраций носителей заряда вблизи перехода. Изменение величины приложенного внешнего напряжения вызывает изменение распределения избыточных носителей вблизи перехода, а следовательно, величины суммарного объёмного заряда. Это явление напоминает процессы в обычном конденсаторе, в котором изменение напряжения, приложенного к обкладкам, вызывает изменение накопленного заряда по закону ∆q=С∆U. Поэтому принято считать, что р-n-переход обладает емкостными свойствами или просто ёмкостью. Ёмкость р-n-перехода оказывает чрезвычайно важное влияние на его импульсные свойства. Емкостные свойства р-n-перехода различны при прямом и обратном смещениях. Так, при прямом смещении они обусловлены главным образом накоплением избыточных концентраций неосновных носителей заряда в р- и n-областях и характеризуются так называемой диффузионной емкостью, которая определяется выражением
где S – площадь р-n-перехода; pn, np – равновесные концентрации дырок в n-области и электронов в р-области; Lp, Le – диффузионные длины дырок в n-области и электронов в р-области; U – внешнее напряжение, приложенное к р-n переходу; Т – температура полупроводника; k – постоянная Больцмана; е – заряд электрона. Из уравнения (2.1) видно, что с увеличением прямого напряжения (U>0) диффузионная ёмкость р-n-перехода быстро возрастает. При обратном смещении (U<0) диффузионная ёмкость уменьшается, и при достаточно большой величине обратного напряжения ее можно считать равной нулю. При обратном смещении емкостные свойства р-n-перехода обусловлены образованием областей объемных зарядов ионизированных примесных атомов и характеризуются так называемой барьерной ёмкостью, которая для резкого р-n-перехода определяется выражением
где Na, Nд – концентрации атомов акцепторной примеси в р-области и донорной примеси в n-области, соответственно; UK – контактная разность потенциалов р-n перехода; e - относительная диэлектрическая проницаемость полупроводника; e0 – электрическая постоянная. Из выражения (2.2) следует, что барьерная ёмкость тем больше, чем выше концентрации примесей в полупроводнике и чем меньше напряжение, приложенное к переходу. Учитывать барьерную ёмкость особенно важно при достаточно больших обратных смещениях р-n перехода, так как диффузионная емкость при этом практически равна нулю. При прямом смещении барьерная емкость значительно меньше диффузионной.
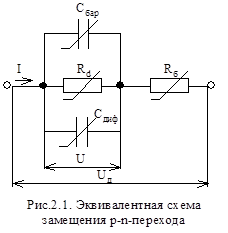
Для анализа динамических процессов в р-n-переходе пользуются его эквивалентной схемой замещения, представленной на рис.2.1. Схема содержит два конденсатора Сбар и Сдиф, отражающих барьерную и диффузионную ёмкости р-n-перехода, а также два резистора Rd и Rб. Первый из них отражает электропроводность области объёмных зарядов р-n перехода, а второй – электропроводность р- и n- областей полупроводника, носящих название базы. Характерно, что все элементы в схеме на рис.2.1 являются нелинейными, их параметры зависят от величины и знака приложенного напряжения Uд. Зависимости Сбар и Сдиф от напряжения рассмотрены выше. Сопротивление Rd при большом обратном напряжении велико, т.к. в области объёмных зарядов практически отсутствуют подвижные носители. При подаче на р-n-переход прямого напряжения область объёмных зарядов, во первых, сужается, а во вторых, обогащается подвижными носителями, что приводит к резкому снижению величины Rd. Сопротивление Rб зависит от приложенного напряжения слабее, чем Rd. Тем не менее при обратном смещении оно больше из-за экстракции неосновных носителей, а при прямом смещении оно меньше из-за инжекции неосновных носителей в р- и n-области полупроводника.
Полупроводниковые диоды ВЫПРЯМИТЕЛЬНЫЕ ДИОДЫ.
Выпрямительные диоды являются плоскостными. Площадь перехода определяется расчетным значением (~I a) выпрямленного Ia. На рис.1 приведены ВАХ Ge и Si выпрямительных диодов малой мощности при комнатной и максимально допустимой температуре окружающей среды. Наиболее существенно отличаются обратные ветви приведенных характеристик. Это различие проявляется в характеристике зависимости как обратного I от Uобр. , так и, особенно сильно, от температуры. Обратные ветви указанных характеристик отличаются также от характеристик идеального p-n-перехода.
Причины отличий. Рассматривая p-n-переход при обратном включении, мы считали Iобр. равным тепловому (дрейфовому) току Iт, который не зависит от Uобр.. Поэтому характеристика Iобр. идеального p-n-перехода шла параллельно горизонтальной оси. В реальном p-n-переходе при обратном напряжении кроме теплового тока протекают еще токи термогенерации (Iг) и утечки (Iу). В отличие от Iт, образующегося за счет наличия носителей заряда в p- и n-областях, Iг является следствием возникновения носителей заряда в самом p-n-переходе. Внутри p-n-перехода, как в каждом полупроводнике, при комнатной температуре имеет место ионизация атомов, в результате которой образуется небольшое количество носителей заряда - свободных электронов и дырок (ē и pк). Электрическим полем перехода дырки перебрасываются в p-область, а ē в n-область, повышая, таким образом, Iобр. диода. Поскольку указанные носители заряда возникают за счет тепловой (генерации) энергии, этот ток называется током термогенерации. С повышением Uобр. ширина p-n-перехода повышается и Iг повышается. При повышении температуры Iг также повышается. Iу протекает по поверхности кристалла под действием Uобр. и зависит от наличия на этой поверхности молекулярных или ионных пленок, шунтирующих переход, например, молекул окислов основного материала, молекул газа и т.п. С повышением Uобр. повышается Iу. От температуры Iу практически не зависит. Таким образом Iобр. через VD имеет три составляющие: Iобр. = Iт + Iг + I у Поскольку Iг и I у зависят от Uобр., суммарный ток диода также зависит от приложенного к нему Uобр.. Соотношение между составляющими Iобр. у Ge и Si диодов различно. У Ge диодов при комнатной температуре Iт>>Iг+Iу. Следовательно: 1)изгиб у характеристики Iобр. в начале; 2)при повышении температуры Iобр. сильно повышается. У Si диодов при комнатных температурах очень мал, и поэтому Iг+Iу >>Iт. Причем часто I |
|||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.24.113 (0.02 с.) |

 , которая и является искомой характеристикой состояния микрочастицы. Он назвал ее волновой функцией и предложил уравнение для ее отыскания:
, которая и является искомой характеристикой состояния микрочастицы. Он назвал ее волновой функцией и предложил уравнение для ее отыскания: , (13)
, (13)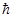 - квант действия;
- квант действия;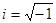 ;
; ;
; :
: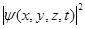 . (14)
. (14) (15)
(15)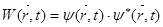 . (16)
. (16) , (17)
, (17) имеет смысл вероятности того события, что в момент времени t одна из микрочастиц находится в единичном объеме, окружающем точку с координатами x1, y1, z1, а другая – в единичном объеме, окружающем точку с координатами x2, y2, z2.
имеет смысл вероятности того события, что в момент времени t одна из микрочастиц находится в единичном объеме, окружающем точку с координатами x1, y1, z1, а другая – в единичном объеме, окружающем точку с координатами x2, y2, z2. , (18)
, (18)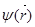 , зависящая только от координат, называется амплитудой волновой функции. Ее можно найти из уравнения
, зависящая только от координат, называется амплитудой волновой функции. Ее можно найти из уравнения , (19)
, (19)

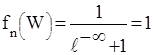
 Энергия для перахода в зону проводимости берется от тепловых колебаний. Поэтому при Т=0°К свободных электронов в полупроводнике нет (ни один уровень в ЗП не занят электроном), все электроны находятся на орбитах (в ВЗ), следовательно, энергетические ЗП соответствуют условию W > WF, а энергетические уровни ВЗ – условию W < WF. Это говорит о том, что уровень Ферми WF расположен ниже «дна» ЗП WП и выше «потолка» ВЗ WВ, т.е. в ЗЗ. На рис. 3 приведены кривые функции Ферми – Дирака.
Энергия для перахода в зону проводимости берется от тепловых колебаний. Поэтому при Т=0°К свободных электронов в полупроводнике нет (ни один уровень в ЗП не занят электроном), все электроны находятся на орбитах (в ВЗ), следовательно, энергетические ЗП соответствуют условию W > WF, а энергетические уровни ВЗ – условию W < WF. Это говорит о том, что уровень Ферми WF расположен ниже «дна» ЗП WП и выше «потолка» ВЗ WВ, т.е. в ЗЗ. На рис. 3 приведены кривые функции Ферми – Дирака. На рис.5,а показана часть кристаллической решетки Ge вблизи узла, замещенного примесным атомом Р. Четыре валентных электрона Р образуют с валентными электронами четырех соседних атомов Ge парноэлектронные ковалентные связи. Поскольку ковалентная связь насыщенная, пятый валентный электрон не участвует ни в одной из четырех связей. Он связан с атомом примеси лишь кулоновскими силами и поэтому его энергетическое состояние более высокое, а энергия связи с атомом значительно меньше квантово – механической энергии связи для остальных четырех электронов.
На рис.5,а показана часть кристаллической решетки Ge вблизи узла, замещенного примесным атомом Р. Четыре валентных электрона Р образуют с валентными электронами четырех соседних атомов Ge парноэлектронные ковалентные связи. Поскольку ковалентная связь насыщенная, пятый валентный электрон не участвует ни в одной из четырех связей. Он связан с атомом примеси лишь кулоновскими силами и поэтому его энергетическое состояние более высокое, а энергия связи с атомом значительно меньше квантово – механической энергии связи для остальных четырех электронов.
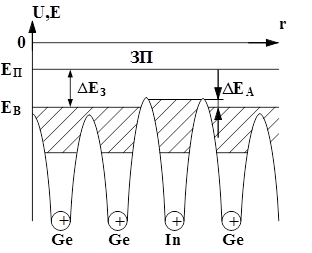
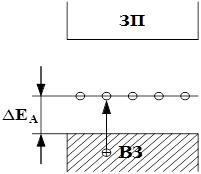 Рис. 6,в. Энергетическая диаграмма р-полупроводника.
Рис. 6,в. Энергетическая диаграмма р-полупроводника.
 При безизлучательной (фононной) рекомбинации избыточная энергия выделяется в виде фононов. Оценки показывают, что максимальная энергия фононов в кристаллах не превышает 0,1 эВ. Это означает, что при рекомбинации через запрещенную зону шириной порядка 1 эВ должно произойти одновременно испускание большого числа фононов. Следовательно, межзонная безизлучательная рекомбинация через относительно широкую запрещенную зону должна быть многофононной. Известно, что вероятность многофононных процессов быстро падает с увеличением числа фононов, участвующих в процессе. Это означает, что в полупроводниках с широкой запрещенной зоной межзонная фононная рекомбинация является также маловероятной.
При безизлучательной (фононной) рекомбинации избыточная энергия выделяется в виде фононов. Оценки показывают, что максимальная энергия фононов в кристаллах не превышает 0,1 эВ. Это означает, что при рекомбинации через запрещенную зону шириной порядка 1 эВ должно произойти одновременно испускание большого числа фононов. Следовательно, межзонная безизлучательная рекомбинация через относительно широкую запрещенную зону должна быть многофононной. Известно, что вероятность многофононных процессов быстро падает с увеличением числа фононов, участвующих в процессе. Это означает, что в полупроводниках с широкой запрещенной зоной межзонная фононная рекомбинация является также маловероятной.
 а) структура
а) структура
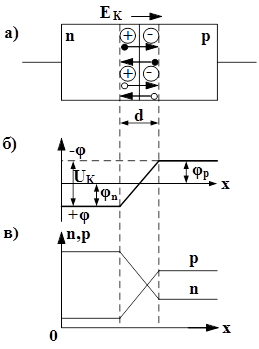 Рис. 3. Образование потенциального барьера р-n-перехода.
Рис. 3. Образование потенциального барьера р-n-перехода.
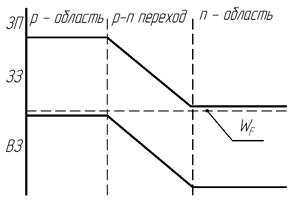 б) энергетическая диаграмма
Рис.2. р-n переход в состоянии термодинамического равновесия
б) энергетическая диаграмма
Рис.2. р-n переход в состоянии термодинамического равновесия

 , (2.1)
, (2.1) , (2.2)
, (2.2)