
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила распространения импульсного процессаСодержание книги
Поиск на нашем сайте
Модель импульсного процесса – это кортеж <Ф, Q, PR>, где Ф – функциональный граф, Q = Q(n) – последовательность возможных воздействий, PR – правило изменения характеристик факторов. Правило распространения возмущающего воздействия воздействия (импульса) в модели может быть аддитивным, мультипликативным и функциональным. Выбор правила зависит от сущности моделируемой ситуации или процесса. Рассмотрим аддитивное правило распространения импульса в когнитивной модели. Приращение значений характеристики с номером j за единицу времени будем называть импульсом в вершине j и обозначать: Pj(t)=Uj(t)-Uj(t-1) (1.5.1) где Uj(t), Uj(t-1) –значения характеристики с номером j в моменты времени t и (t-1) соответственно; Зададим формализованное правило развития в модели импульсного процесса (считаем, что импульс в вершине возникает мгновенно), следующим образом: 1. Изменения значений характеристик происходят только в дискретные моменты времени t, t = 0, 1, 2, … 2. Возникший в j -й вершине импульс Pj(t) в момент времени t передается за единицу времени и только в смежные вершины в момент t + 1. По дугам передаются только импульсы, а не полные значения характеристик. 3. Импульс Pj(t) в j -й вершине передается в смежные вершины с коэффициентом усиления, равным весу дуг, соединяющих смежные вершины. 4. Импульсы, одновременно пришедшие в i -ю вершину из смежных с нею вершин, складываются алгебраически, т.е. с учетом знаков: Pi(t) = где zji – вес дуги из вершины j, смежной с вершиной i, Pj (t – 1) – импульс в j -й вершине в момент t – 1; Gi – множество номеров вершин j, смежных с вершиной i; т.е. тех, из которых в i -ю вершину имеется дуга; соответственно
Расчеты в моделях опираются на теорему Робертса. Величина вектора-импульса
где P (0) – вектор-строка; Zt – t -я степень матрицы весов данного орграфа. Простейшим вариантом распространения возмущения является случай, когда вектор P(0) имеет одну ненулевую компоненту (один ненулевой вход, т.е. возмущение поступает только в вершину Ui). Такие процессы называют простыми процессами распространения возмущения. ВОПРОСЫ К ГЛАВЕ 1 1. Дайте определение СЭПП; 2. Дайте определение когнитивной карты СЭПП; 3. Охарактеризуйте основные методы построения когнитивных карт;
4. Дайте определение когнитивной модели; 5. В чем отличие когнитивной модели от когнитивной карты? 6. Каким правилом задается динамика отношений в модели? 7. Что называется путем в ориентированном графе? Что такое контур? 8. В чем состоит анализ когнитивных карт? Какие свойства исследуемого процесса можно определить по наличию положительных (отрицательных) контуров в когнитивной карте?
|
|||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.164.100 (0.006 с.) |

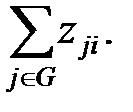 Pj (t - 1) (1.5.2)
Pj (t - 1) (1.5.2)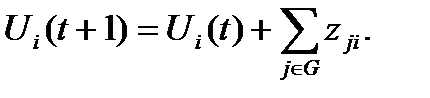
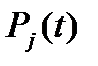 (1.5.3)
(1.5.3) в орграфе определяется по формуле
в орграфе определяется по формуле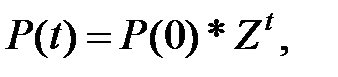 (1.5.4)
(1.5.4)


