
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
СуперПоверхности 2-го порядкаСодержание книги
Поиск на нашем сайте
На основе использования синусо-косинусоидального способа кинематического построения поверхностей 2-го порядка возможно создание более сложных поверхностей путем введения степенного показателя для функций синуса и косинуса и, таким образом, получить класс аналитических уравнений суперповерхностей. Путем изменения значения степени (может быть целой и дробной величиной) функций синуса и косинуса поверхности 2-го порядка трансформируются в поверхности высших порядков и, если параметрическую форму уравнений приводить к алгебраической, то получим алгебраические уравнения с дробными степенями. Все кинематические модели суперповерхностей 2-го порядка отличаются от кинематических моделей классических поверхностей 2-го порядка только наличием степенного показателя при функциях синуса и косинуса, поэтому приведем только модель суперсферы и примеры трансформации всех поверхностей 2-го порядка. Кинематическая модель суперсферы (суперэллипсоида) Модель представлена системой уравнений
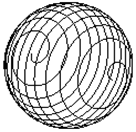
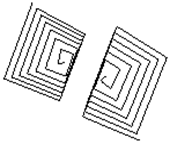
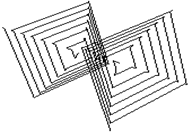
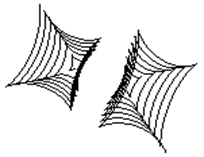
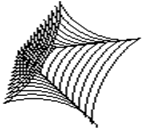
y = Ö(b 2- z 2) ´ cosр(80z), z = - N, …, N. При p равном единице кинематическая модель суперповерхности становится кинематической моделью классической поверхности 2-го порядка. При увеличении p сфера сжимается с четырех сторон – при фронтальном рассмотрении это будет выглядеть как действие некой силы под углами в 45, 135, 225 и 315 градусов. Если же p уменьшается в диапазоне от 1 до 0, то действие этой силы изменит направление на противоположное. Этот осуществляется за счет стягивания точек фигуры по диагональным направлениям. При устремлении p к бесконечности фигура принимает крестообразное очертание, а при p равном нулю точки поверхности «разносятся» по углам и промежуточные значения координат точек остаются незанятыми. При этом, получается что сфера теряет свою целостность. Чтобы избежать этого нежелательного эффекта, здесь применяется построение по вычисляемым координатам не примитива точки, а ломаной линии. При этом если точки будут стоять рядом друг с другом, то получаемая пространственная кривая будет плавной. Важно заметить, что, несмотря на ощущение угловатости, суперповерхность не имеет изломов и остается плавной и непрерывной. Рассмотрим суперповерхности при различных значениях p. Суперсфера, построенная с крупным шагом, с показателем p равным 0, 0.5, 1, 2, 3 и 5 показана на рис.1.46 – рис.1.51 соответственно. На рис.1.52 – рис.1.54 показана суперсфера, построенная с малым шагом, с показателем p равным 0, 2, 5 соответственно.
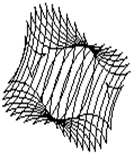
Остальные суперповерхности 2-го порядка построены с показателем p равным 0, 2, 3. Однополостный супергиперболоид, построенный с крупным шагом, показан на рис.1.55 – рис.1.57 соответственно, с малым шагом показан на рис.1.58 – рис.1.60 соответственно.
Двуполостный супергиперболоид, построенный с крупным шагом, показан на рис.1.61 – рис.1.63 соответственно, с малым шагом показан на рис.1.64 – рис.1.66 соответственно.
Рис. 1.64 Рис. 1.65 Рис. 1.66
Рис. 1.67 Рис. 1.68 Рис. 1.69
Рис. 1.70 Рис. 1.71 Рис. 1.72
Суперпараболоид, построенный с крупным шагом, показан на рис.1.73 – рис.1.75 соответственно, с малым шагом показан на рис.1.76 – рис.1.78 соответственно.
Рис. 1.73 Рис. 1.74 Рис. 1.75
Рис. 1.76 Рис. 1.77 Рис. 1.78
Рис. 1.79 Рис. 1.80 Рис. 1.81
Рис. 1.82 Рис. 1.83 Рис. 1.84
В алгебраической форме система уравнений для суперповерхностей при p = 5 имеет следующий вид: Суперсфера
Супергиперболоид
Особенностью алгебраических уравнений суперповерхностей 2-го порядка является порядок степеней не выше 2. Однако наличие дробных степеней говорит о том, что в данном случае это уравнение 10-ой степени. Если это уравнение привести к общему виду с целочисленными показателями, то такая операция приведет из огромного многообразия поверхностей 10-го порядка к выделенному классу суперповерхностей 2-го порядка, так как из общего числа коэффициентов членов алгебраического уравнения 10-го порядка (286) не равных нулю будут не более 13. Меняя параметры кинематических моделей суперповерхностей или значения коэффициентов членов алгебраических уравнений суперповерхностей с дробными показателями, возможно конструирование сложных по форме технических поверхностей.
Преобразование моделей Для геометрического конструирования сложных объектов из графических примитивов и размещения их в пространстве необходимо осуществлять с графическими примитивами и моделями объектов различные преобразования: перенос, поворот, масштабирование и изменение формы. Перенос в пространстве осуществляется путем движения параллельно осям прямоугольной системы координат. Для перемещения точки в пространстве достаточно дать приращения по координатам x, y, z. Формулы переноса
где
Эти формулы впрямую используются для перемещения растровых, точечных и каркасных моделей, так как во всех этих моделях осуществляется перемещение точек. Для перемещения аналитических моделей необходимо преобразовывать коэффициенты уравнений. Выведем формулы преобразования коэффициентов алгебраического уравнения общего вида от 1-го по 3-ий порядок.
Нам необходимо получить новые значения коэффициентов уравнения перемещенной поверхности Всевозможные произведения переменных уравнения после подстановки приращений
Выполнив группировку коэффициентов уравнений от старших к младшему, получим формулы для вычисления новых коэффициентов алгебраического уравнения 3-го порядка после перемещения поверхности в пространстве.
Данный способ получения формул переноса алгебраических поверхностей в пространстве может быть использован для поверхностей любых порядков. Перемещение в пространстве не меняет ориентации поверхности, ее масштабов и не изменяет форму поверхности. Поворот точки в пространстве осуществляется по окружности вокруг осей в плоскостях перпендикулярных оси вращения с радиусом, равным расстоянию от точки до оси вращения. Поворот линии или поверхности в пространстве означает вращение всех точек, принадлежащих графическому объекту, вокруг выбранной оси. Каждая точка графического объекта вращается по своему радиусу. Угол поворота задается в градусах или радианах. Путем вращения вокруг осей прямоугольной системы координат можно достичь любой ориентации графического объекта в пространстве, для этого достаточно выполнить только поворот вокруг двух любых осей системы координат.

Рис.1.85 Вывод формул вычисления координат аналитических моделей графических объектов (как и в случае переноса) осуществляется, методом подстановки формул вращения точки в уравнение, и вычисление новых значений коэффициентов уравнений через прежние коэффициенты и значения углов поворота. В отличие от формул переноса, где можно задавать одновременно перемещение по всем трем осям, повороты осуществляются последовательно вокруг каждой выбранной оси. Опуская громоздкие подстановки, приводим формулы вычисления координат точки и коэффициентов алгебраического уравнения 3-го порядка при выполнении вращения вокруг осей x, y, z. Эти формулы годны для поверхностей и 1-го и 2го порядков, при этом коэффициенты более высокого порядка равны нулю. Поворот вокруг оси x точки c координатами (x, y, z)
где x, y, z - первоначальные координаты точки,
Поворот вокруг оси x алгебраической поверхности 3-го порядка общего вида, где
Поворот вокруг оси y точки c координатами (x, y, z)
где x, y, z - первоначальные координаты точки,
Поворот вокруг оси y алгебраической поверхности 3-го порядка общего вида, где
Поворот вокруг оси z точки c координатами (x, y, z)
где x, y, z - первоначальные координаты точки,
Поворот вокруг оси z алгебраической поверхности 3-го порядка общего вида, где
Данный способ получения формул поворота алгебраических поверхностей в пространстве может быть использован для поверхностей любых порядков. Выведенные формулы справедливы для вращения вокруг осей прямоугольной системы координат (центр вращения находится в начале системы координат). В случае если вам необходимо вращать объект вокруг оси, произвольно расположенной в пространстве, то необходимо ось вращения совместить с осью системы координат путем переноса и поворота, а после выполнения вращения вернуть ось вращения в прежнее положение. Практически это делается следующим образом. В объекте выбирается точка, лежащая на оси вращения, эта точка переносится в начало системы координат. Затем на оси вращения выбирается вторая точка, которая путем вращения совмещается с выбранной осью системы координат. После выполнения заданного поворота объекта, возвращаем положение оси вращения объекта в первоначальное положение, последовательно повернув и перенося ось объекта. Данный способ поворота в пространстве не меняет местоположение поверхности, ее масштабов и не изменяет форму поверхности. Масштабирование – это увеличение или уменьшение размеров объекта в определенное число раз по отношению к оригиналу. Масштаб записывается отношением двух чисел, где оригинал всегда представлен 1, а масштабированный объект представлен любым числом больше единицы (М), том числе и дробным. Масштаб увеличения записывается как М:1, а масштаб уменьшения как 1:М. Масштабирование всегда осуществляется относительно какой-либо точки (центра масштабирования). В прямоугольной системе координат это означает увеличение или уменьшение координат точек в определенное число раз по отношению к началу системы координат. Равномерное масштабирование означает одинаковое масштабирование по всем трем осям системы координат. Для симметричных объектов такое масштабирование не меняет формы объекта, если центр масштабирования совпадает с центром симметрии, а меняет только размер объекта. Неравномерное масштабирование (разные масштабы для осей системы координат) приводит к изменению формы объекта. Но в этом случае меняется не тип объекта, а образуется подтип объекта. Например, если сферу с центром, расположенным в начале системы координат, масштабировать только по одной оси системы координат, то получим двухосный эллипсоид, по двум с разными масштабами получим трехосный эллипсоид. Все эти поверхности относятся к одному типу - сферические поверхности, однако будут разных подтипов. Общепринятое масштабирование относится к линейным преобразованиям, но, если вместо числа масштаба поставить функцию, то можно выполнять нелинейное масштабирование и это приведет к изменению типов поверхностей. Формулы масштабирования для точки увеличение
уменьшение
где
Масштабирование точки при увеличении масштаба приводит к удалению точки от начала системы координат, а при уменьшении масштаба точки приводит к приближению точки к началу системы координат. Способом подстановки получим формулы масштабирования для коэффициентов уравнения 3-го порядка, имея в виду, что уравнение общего вида имеет коэффициенты, которые обратно пропорциональны коэффициентам приведенного уравнения. Это означает, что при масштабировании поверхностей, описанных алгебраическими уравнениями общего вида, значения масштабов при вычислении значений коэффициентов алгебраического уравнения общего вида меняются местами, по сравнению с вычислением координат точки. Увеличение размеров объекта
уменьшение значений коэффициентов алгебраического уравнения общего вида приводит к увеличению размеров объекта. Уменьшение размеров объекта
увеличение значений коэффициентов алгебраического уравнения общего вида приводит к уменьшению размеров объекта. Масштабирование плоскости, расположенной в начале системы координат с любой ориентацией, не имеет смысла, так как нормаль плоскости равна нулю. Если нормаль имеет какое либо числовое значение, то увеличение масштаба плоскости удаляет плоскость от начала системы координат, а уменьшение масштаба плоскости приближает плоскость к началу системы координат, не меняя при этом ориентации в пространстве, так как при масштабировании сохраняются соотношения коэффициентов уравнения плоскости Сравнение моделей При моделировании графических объектов и сцен немаловажное значение имеет объем записи моделей в компьютер и сложность алгоритмов их обработки. Особое значение этот вопрос приобретает в случае передачи моделей по сетям связи в реальном времени, поэтому в таблицу сравнения включены изображения с применением стандартов сжатия графических изображений. Для сравнения различных моделей было подсчитано значение объемов необходимой памяти для каждой модели с целью записи многоцветного объекта, состоящего из одной поверхности 2-го порядка. Была выбрана поверхность - окрашенный в цвета радуги двухосный эллипсоид (рис.1.86), размером 200 х 180 х 180 мм. Эллипсоид размещен в центре сцены размером 256х192х192 мм. Шероховатость его поверхности не должна превышать 0,01 мм.
Рис.1.86 Данные сравнения приведены в таблице 1.5. При вычислении коэффициента сжатия, за 1 был принят объем записи изображения в стандарте TIFF. Таблица 1.5
На примере эксперимента с одной поверхностью нужно аккуратно подходить к обобщающим выводам, однако можно оценить порядок объемов записей изображений и различных моделей, принимая во внимание, что реальные объекты, как правило, состоят из большого числа примитивов. Преимущество аналитических моделей перед растровыми, точечным и каркасными заключается в описании непрерывных абсолютно тонких и бесконечно точных поверхностей в компактной форме (табл.1.5), но визуализация их представляет собой довольно сложный и вычислительно трудоемкий процесс. Применение многих эффективных методов вычислительной математики все равно ставит под сомнение возможность визуализации таких поверхностей в реальном времени на существующей вычислительной технике. Требуются либо эффективные аппаратные решения (увеличение производительность процессоров, создание специальных геометрических процессоров параллельной обработки частей изображений вплоть до пиксела), либо на определенном этапе преобразовывать с выбранной точностью аналитические модели в каркасные (векторные) модели, что даст возможность использовать существующие графические приложения, работающие с векторными моделями. Однако необходимо отметить, что любые преобразования одних моделей в другие должны быть обоснованы, как правило, они ведут к потере информации.
КОНСПЕКТ ЛЕКЦИЙ по дисциплине «Компьютерная геометрия и графика» Лекция 3 Тема 4 - Компьютерная реализация геометрического моделирования Формирование графических объектов из примитивов При моделировании сцены необходимо иметь набор объектов, которые будут размещены в сцене. Можно выбирать объекты из библиотек графических приложений и использовать их без изменений, можно библиотечные объекты модифицировать, можно создавать объекты из графических примитивов. Существующие графические приложения, как правило, содержат небольшой набор стандартных объектов, таких как сфера, куб, конус, цилиндр, тор. Непосредственное использование библиотечных объектов дает мало возможностей для создания многообразных сцен. Модификация стандартных объектов позволяет расширить эти возможности, но они также ограничены. Создание объектов из примитивов, таких как точка, линия и поверхность значительно расширяет круг многообразных объектов, однако этот процесс часто бывает длительным и трудоемким. Например, формирование растровых и точечных моделей требует ручной записи множества пикселов, вокселов и точек. Формирование каркасных моделей снижает число задаваемых точек (линий), однако при высокой точности описания кривых поверхностей, их еще достаточно много. Аналитические модели в определенной степени решают проблему записи поверхностей, так как число коэффициентов уравнений даже высших порядков невелико (Приложение 2). Однако в настоящее время графические приложения не содержат библиотек алгебраических поверхностей высших порядков, которые дают огромное многообразие любых поверхностей (Приложение 3). Процесс формирования объектов из примитивов сводится к масштабированию, перемещению, повороту примитивов и выбору частей примитивов, которые принадлежат объекту (Приложение 4). Алгебраические модели дают много возможностей формировать путем составления из примитивов сложных поверхностей и иметь при этом компактные описания. Например, из шести плоскостей можно составить описание куба. Для этого, достаточно перемножить уравнения шести плоскостей (
Уравнение 4-го порядка
Рис.1.87 Рис.1.88
Процесс формирования сцены заключается в размещении и ориентации объектов в сцене. Анимация - создание кадров видео фильма, в котором отображаются динамичные объекты (перемещаются, поворачиваются, изменяются). При моделировании анимации записываются формулы движений и изменений объектов для каждого кадра видео фильма (Приложение 5). Перемещение, повороты и масштабирование объектов моделируются с использованием соответствующих формул одновременно для всех примитивов, составляющих объект. Изменение формы объекта необходимо для формирования библиотек объектов, при проектировании сложных конструкций, при моделировании сложных процессов, в которых происходят геометрические изменения (взрывы, разрушения, столкновения, деформация и т.п.). Изменение формы объектов достигается следующими способами: - перемещением и поворотом в пространстве отдельных примитивов, составляющих объект; - неравномерным масштабированием из произвольно выбранной точки объекта; - изменением значений параметров для аналитических выражений (для алгебраических поверхностей изменением значений коэффициентов алгебраических уравнений). При изменении формы объекта необходимо решать следующие задачи: - определять линии пересечения поверхностей; - осуществлять сшивку и сглаживание поверхностей. Для растровых, точечных и каркасных моделей изменения объектов сводятся к операциям с элементами растра и точками, которые перемещаются в пространстве. Здесь решается задача заполнения разрывов в поверхности объекта (которые могут возникнуть) дополнительными элементами растра или точками (для точечных и каркасных моделей). Для аналитических моделей, например, для алгебраических моделей произвольные изменения коэффициентов могут привести к получению мнимых поверхностей (отсутствие решений уравнений). В этом случае необходим аналитический или визуальный контроль выполнения изменений. Если для растровых, точечных и каркасных моделей результат изменения объекта можно предположить, то в случае изменения отдельных коэффициентов алгебраических уравнений высших порядков полученный результат может быть неожиданным. Приведем пример, как изменение коэффициентов алгебраического уравнения 4-го порядка влияет на изменение формы поверхности. Возьмем поверхность 4-го порядка «Две сферы» (рис.1.89), уравнение
Рис. 1.89 Рис. 1.90
Рис. 1.91 Рис. 1.92 Так как все изменения происходят в прямоугольной системе координат, наиболее понятные изменения можно проводит по осям системы координат, при необходимости перенося объект в начало системы координат и потом поворачивая объект для совмещения направления изменений с осями системы координат, а затем, возвращая объект в прежнее положение.
Визуализация графических объектов Визуализация - это одна из наиболее сложных проблем компьютерной графики. Визуализация предусматривает процесс преобразования компьютерной модели в изображение на экране дисплея или на бумаге с необходимой точностью воспроизведения, с удалением невидимых линий, с выполнением разрезов, сечений, с освещением и нанесением теней и поясняющей текстовой или графической информацией. Чтобы трехмерную модель, сформированную в процессе моделирования в памяти компьютера, отобразить, необходимо преобразовать ее в двухмерную модель (видео модель) и затем в страницу отображения с соответствующим разрешением изображения и таблицей цветов. При визуализации в практике, в основном, используются два вида проецирования: - метод параллельного ортогонального проецирования, который наиболее подходит для технического конструирования, так как не вносит искажений размеров объектов при отображении на плоском экране; - метод центрального проецирования, дающий при визуализации реалистических сцен на плоский экран эффект глубины сцен за счет изменения реальных размеров объектов в зависимости от глубины расположения объектов в сцене. При отображении могут быть использованы различные виды проецирования и получены различные типы изображений (рис.2.1). Параллельное ортогональное |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.231.160 (0.01 с.) |

 x = Ö(a 2- z 2) ´ sinр(80z),
x = Ö(a 2- z 2) ´ sinр(80z),


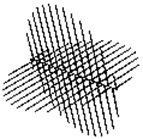












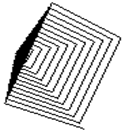 Суперконус, построенный с крупным шагом, показан на рис.1.67 – рис.1.69 соответственно, с малым шагом показан на рис.1.70 – рис.1.72 соответственно.
Суперконус, построенный с крупным шагом, показан на рис.1.67 – рис.1.69 соответственно, с малым шагом показан на рис.1.70 – рис.1.72 соответственно.



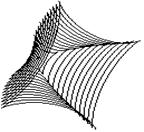
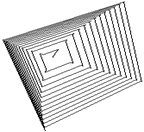



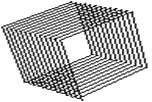

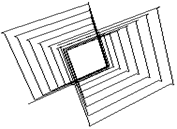
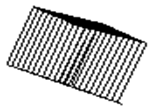 Суперцилиндр, построенный с крупным шагом, показан на рис.1.79 – рис.1.81 соответственно, с малым шагом показан на рис.1.82 – рис.1.84 соответственно.
Суперцилиндр, построенный с крупным шагом, показан на рис.1.79 – рис.1.81 соответственно, с малым шагом показан на рис.1.82 – рис.1.84 соответственно.


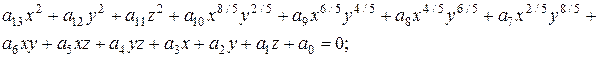
 Суперцилиндр
Суперцилиндр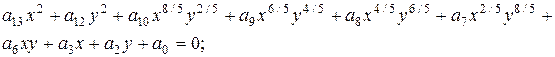
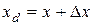 ;
; 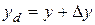 ;
; 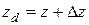 ,
,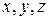 - координаты прежнего положения точки;
- координаты прежнего положения точки;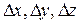 - приращения координат;
- приращения координат; - координаты нового положения точки.
- координаты нового положения точки.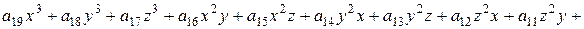
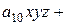
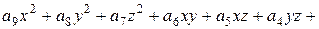

 , выраженные через коэффициенты уравнения поверхности первоначального положения
, выраженные через коэффициенты уравнения поверхности первоначального положения 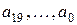 .
.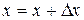 ;
; 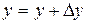 ;
; 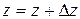 ; будут иметь вид:
; будут иметь вид: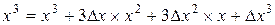 ;
;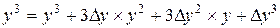 ;
;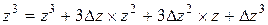 ;
;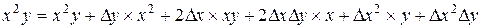 ;
;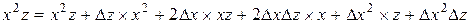 ;
;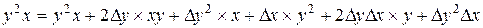
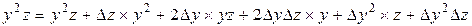
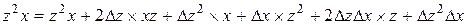 ;
;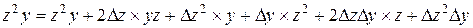 ;
;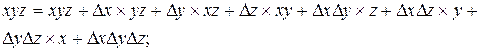
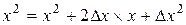 ;
; ;
;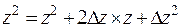 ;
;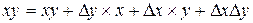 ;
; ;
;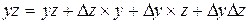 .
.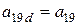 ;
; 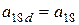 ;
;  ;
; 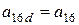 ;
;  ;
;  ;
;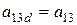 ;
; 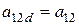 ;
; 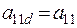 ;
; 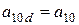 ;
;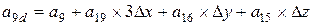 ;
; ;
;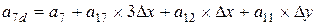 ;
;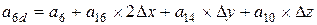 ;
;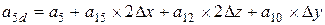 ;
;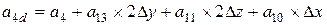 ;
;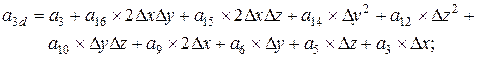
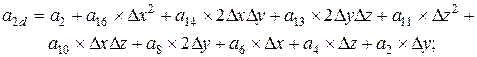 ;
;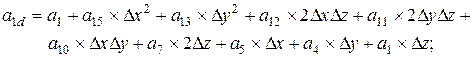 ;
;
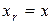 ;
;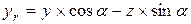 ;
;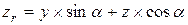 ,
,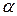 - угол поворота вокруг оси x,
- угол поворота вокруг оси x, - координаты повернутой точки.
- координаты повернутой точки. - первоначальные значения коэффициентов уравнения,
- первоначальные значения коэффициентов уравнения,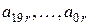 - значения коэффициентов уравнения после поворота,
- значения коэффициентов уравнения после поворота, ;
;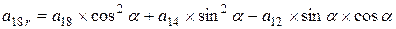 ;
;
 ;
;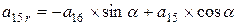 ;
;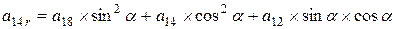 ;
;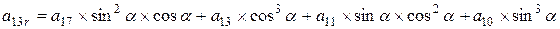 ;
; ;
;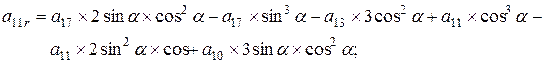

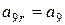 ;
;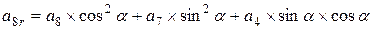 ;
;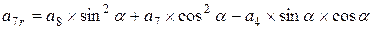 ;
;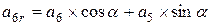 ;
;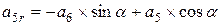 ;
;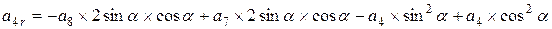 ;
; ;
; ;
;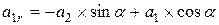 ;
;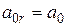 .
. ;
;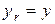 ;
;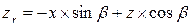 ,
,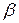 - угол поворота вокруг оси y,
- угол поворота вокруг оси y,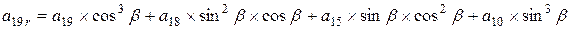 ;
;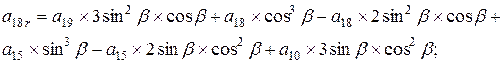 ;
;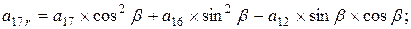
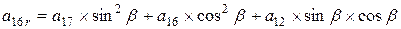 ;
;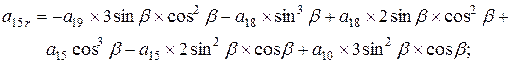
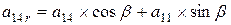 ;
;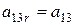 ;
;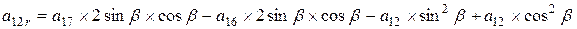 ;
; ;
;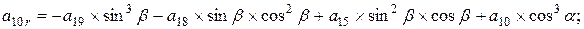
 ;
;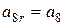 ;
;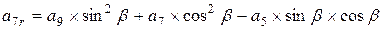 ;
; ;
;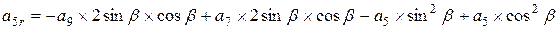 ;
;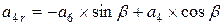 ;
;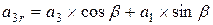 ;
;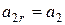 ;
; ;
;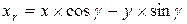 ;
;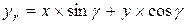 ;
;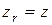 ,
,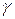 - угол поворота вокруг оси z,
- угол поворота вокруг оси z,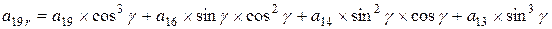 ;
;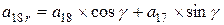 ;
;
 ;
;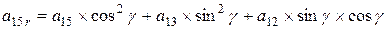 ;
;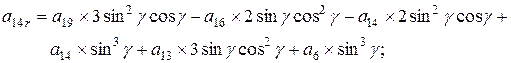
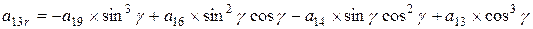 ;
;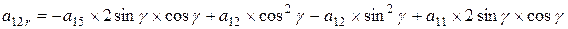 ;
; ;
; ;
; ;
;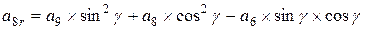 ;
; ;
;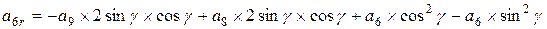 ;
; ;
; ;
;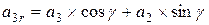 ;
;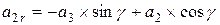 ;
;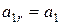 ;
;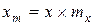 ;
; 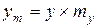 ;
; 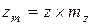 ,
, ;
; 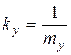 ;
; 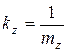 ;
;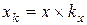 ;
; 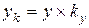 ;
; 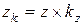 ,
, - новые координаты масштабированной точки;
- новые координаты масштабированной точки;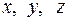 - первоначальные координаты точки;
- первоначальные координаты точки;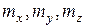 - значения масштаба увеличения по осям соответственно;
- значения масштаба увеличения по осям соответственно;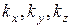 - значения масштаба уменьшения по осям соответственно.
- значения масштаба уменьшения по осям соответственно.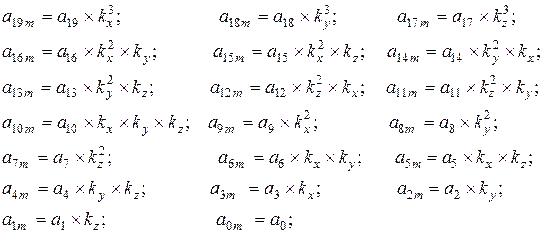
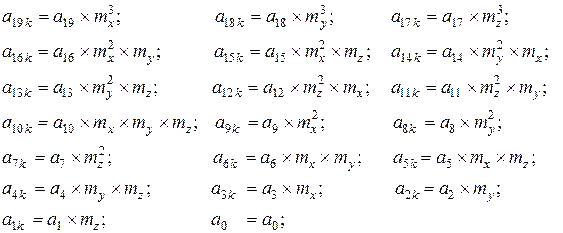
 , а меняется только значение коэффициента
, а меняется только значение коэффициента 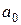 , который определяет значение нормали плоскости.
, который определяет значение нормали плоскости.
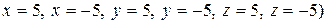 , чтобы получить уравнение 6-го порядка
, чтобы получить уравнение 6-го порядка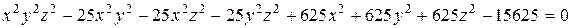 , которое описывает куб с размером 5 единиц (рис.1.87). Достаточно поставить точку выбора в центре куба, чтобы получить привычный куб при условии ограничения поверхности куба плоскостями (выбор частей плоскостей).
, которое описывает куб с размером 5 единиц (рис.1.87). Достаточно поставить точку выбора в центре куба, чтобы получить привычный куб при условии ограничения поверхности куба плоскостями (выбор частей плоскостей).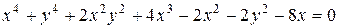 ,
,
 полученное путем перемножения коэффициентов двух уравнений круговых цилиндров 2-го порядка, смещенных в пространстве (рис.1.88), описывает довольно интересную поверхность.
полученное путем перемножения коэффициентов двух уравнений круговых цилиндров 2-го порядка, смещенных в пространстве (рис.1.88), описывает довольно интересную поверхность.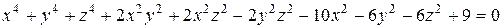 которой было получено методом объединения двух сфер. Будем менять значения коэффициентов уравнения. Если коэффициент при y 2 равный -6 изменить на -34, то получим сглаженную поверхность, где исчезла резкая граница при пересечении сфер (рис.1.90). Если коэффициент при y2 равный -6 изменить на +15, то получим разрыв поверхности и искажение форм сфер (рис.1.91). Если коэффициент при x 2 y 2 равный 2 изменить на -3, то получим другую поверхность (рис.1.92).
которой было получено методом объединения двух сфер. Будем менять значения коэффициентов уравнения. Если коэффициент при y 2 равный -6 изменить на -34, то получим сглаженную поверхность, где исчезла резкая граница при пересечении сфер (рис.1.90). Если коэффициент при y2 равный -6 изменить на +15, то получим разрыв поверхности и искажение форм сфер (рис.1.91). Если коэффициент при x 2 y 2 равный 2 изменить на -3, то получим другую поверхность (рис.1.92).






