
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема №1. Аксиоматическая теория .Содержание книги
Поиск на нашем сайте
1.1. К неопределяемым понятиям аксиоматического построения геометрии относятся…
1.2.Из приведенных высказываний истинным является следующее… · · · ·
1.3. Среди предложенных математических утверждений аксиомой является следующие… Если две прямые параллельны третьей, то они параллельны. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой. Тема №2. Теория множеств. 2.1 Установите соответствие между множествами и верными для них высказываниями. · множество бесконечно 3 · · · 2. 2 Установите соответствие между множествами и верными для них высказываниями. 1. А – множество студентов первого курса; В – множество студентов 2. А – множество студентов; В – множество людей, умеющих водить машину 3. А – множество кошек; В – множество собак
другого - 2 2.3 Установите соответствие между множествами и верными для них высказываниями.
· · · 2.4.
2.5. Даны два множества:
· · · · 2.7 Даны множества · · · · 1.8. Заданы множества
1.9. Заданы произвольные множества А, В и С. Расположите указанные справа множества так, чтобы каждое из них было подмножеством следующего за ним.
1.10. Если отношение задано неравенством:
1.11. Даны множества M={ a, b, c, d} и N={b, c, d, e, f, g}. Установите соответствия между обозначениями множеств и самими множествами. 1. M Множества: {a} - 3 {b, c, d} - 1 {a, b, c, d, e, f, g} - 2 {e, f, g} - 4 11.12. Заданы множества {(4, 6), (6, 4), (6, -4), (-6, -4), (4, -6), (-4, 2)} {-6, -4, 2, 4, 6} { {(2, 4), (2, -4), (6, 4), (6, -4), (-6, 4), (-6, -4)} истина 11.13. Принято обозначать:
11.14. Заданы произвольные множества А, В и С. Расположите указанные справа множества так, чтобы каждое из них было подмножеством следующего за ним.
11.15 Даны множества N={ a, b, c, d, e, f, g} и K={a, b, c, d, e}. Установите соответствия между обозначениями множеств и самими множествами.
1. N 2. N 3. N\K 4. K\N Множества: {a, b, c, d, e} 1 {a, b, c, d, e, f, g} 2 {f, g} 3 { } 4 11.16 Заданы множества {(1,-a), (1, в), (-3,-а), (-3, в)} - истина {(-а,1),(в,-3),(в,1),(-а,-3)} {-а, в, 1, -3} { 11.17. Заданы множества {(8,5), (8,6), (3,5), (3,6)} - истина {(5, 8), (5, 3), (6, 8), (6, 3)} {3, 5, 6, 8} { Тема №3. Комбинаторика 3.1 П Из цифр числа 4689 можно составить различные трехзначные числа, в которых цифры не повторяются. Всего таких чисел будет... 60р24 Оа24 3.2 Число различных перестановок из букв слова «зачет», в которых буква «з» стоит на первом месте, а буква «т» на последнем месте, равно… 6.
3.3 Количество различных способов выбора (порядок не имеет значения) 2 различных учебников по математической логике из 6 различных, имеющихся в библиотеке, равно… 15 С 2/6
3.4 Количество перестановок из букв слова «вальс», в которых буква «в» на первом месте, а буква «с» - в конце слова, равно…
3.5. Количество перестановок из букв слова «лидер», в которых буква «е» на первом месте, а буква «д» - в конце слова равно…. 6 3.6..Количество перестановок из букв слова «вирус», в которых буква «в» на первом месте равно…. 24
3.7. Количество перестановок из букв слова «время», в которых буква «я» на первом месте равно…. 24
Тема № 4. Алгебра высказываний.
4.2 Даны высказывания: А = «Озеро Байкал является самым чистым озером в мире» и В = «Чайковский написал 10 опер». Дизъюнкцией этих высказываний является предложение…
4.3. Высказывание A – «Джон фон Нейман – архитектор ЭВМ»; высказывание В – «Диагонали прямоугольника равны». Конъюнкцией этих высказываний (
4.4.. Известно, что длина прямоугольника
4.5. Высказывание A – «Алгебра логики изучает высказывания»; высказывание В – «Сумма углов треугольника равна
4.6. Высказывание A – «Принтер – это устройство вывода информации»; высказывание В – «Две параллельные прямые не имеют общих точек». Дизъюнкцией этих высказываний (
|
|||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.52.109 (0.01 с.) |


 В аксиомах идет речь об основных математических понятиях, таких как «точка», «прямая», «плоскость».
В аксиомах идет речь об основных математических понятиях, таких как «точка», «прямая», «плоскость». – множество натуральных чисел,
– множество натуральных чисел, – множество целых чисел,
– множество целых чисел, – множество рациональных чисел,
– множество рациональных чисел, – множество действительных чисел.
– множество действительных чисел.
 – интервал числовой оси;
– интервал числовой оси;  – отрезок числовой оси. Тогда для них истинными высказываниями являются…
– отрезок числовой оси. Тогда для них истинными высказываниями являются… Истина
Истина  Истина
Истина 
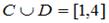

 B=A Истина
B=A Истина C=
C=  Истина
Истина и
и  . Тогда истинными высказываниями являются…
. Тогда истинными высказываниями являются… Истина
Истина

 Истина
Истина и
и  . Верным для них будет утверждение…
. Верным для них будет утверждение… 1
1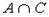 2
2 4
4 , то данному отношению принадлежит следующие пары чисел…
, то данному отношению принадлежит следующие пары чисел…

 истина
истина  N
N N
N {2,6,-6} и
{2,6,-6} и  {4,-4}, тогда декартовым произведением этих множеств АВ является множество…
{4,-4}, тогда декартовым произведением этих множеств АВ является множество… }
} истина
истина


 2
2 5
5 6
6 1
1 3
3 4
4 K
K K
K {1,-3} и
{1,-3} и  {-а, в}, тогда декартовым произведением этих множеств А´В является множество …
{-а, в}, тогда декартовым произведением этих множеств А´В является множество … }
} ) является предложение …
) является предложение … см, ширина –
см, ширина –  см. Тогда истинными высказываниями являются следующие…
см. Тогда истинными высказываниями являются следующие… ». Конъюнкцией этих высказываний (
». Конъюнкцией этих высказываний ( ) является предложение …
) является предложение … ) является предложение …
) является предложение …


