Расчет барьерной ёмкости p-n переходов.

Для решения задач необходимо ознакомиться соответствующими разделами теоретического материала [1-4].

Обедненные слои в областях n- и p- типов полупроводников имеются при отсутствии напряжения на переходе, их толщины возрастают с ростом величины обратного смещения на p-n переходе. Если уподобить обедненный слой диэлектрику плоского конденсатора, то емкость такого конденсатора

 

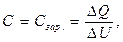
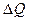где – изменение заряда неподвижных ионов в обедненных слоях, прилегающих к p-n переходу, а 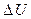– изменение напряжения на переходе. Эта емкость называется зарядной (или барьерной, или запорной), она используется в полезных целях, т.к. при обратном смещении, в отличие от прямого, емкость не зашунтирована малым активным сопротивлением перехода. Поэтому расчет зарядной емкости практически важен, подобные расчеты проводятся при разработке и проектировании емкостных элементов интегральных микросхем, а также необходимы для оценки быстродействия диодов и транзисторов. Так, в биполярном транзисторе ёмкость р-п перехода база-коллектор в нормальном активном режиме находится под обратным напряжением, в схемах включения с общей базой и общим эмиттером она является выходной ёмкостью. R-C цепочка на выходе транзистора определяет его быстродействие.

Рассмотрим примеры решения задач.

Задача 5.1.

Резко выраженный (ступенчатый) p-n переход транзистора изготовлен из легированного германия с концентрацией акцепторной и донорной примесей в его областях соответственно и . При обратном смещении величина максимального электрического поля в переходе составляет . Требуется определить толщину обедненного слоя, удельную зарядную емкость p-n перехода и полную зарядную емкость, если площадь перехода .

Решение.

Максимальная величина напряженности электрического поля в области p-n перехода определяется исходя из уравнения Пуассона. В одномерном случае

.

 

Максимальное значение напряженности

 

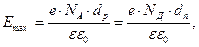
где и – толщины обедненного слоя в p- и n- областях соответственно, и 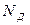– концентрации примесей в p- и n- областях, 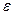- относительная диэлектрическая проницаемость материала полупроводника ( 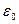= 16 для германия), – электрическая постоянная вакуума, 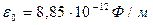, e – заряд электрона, .

Из последнего выражения находим толщины обедненных слоев в p- и n- областях р-п перехода

 

;

 

.

Полная толщина обедненного слоя представляет собой сумму толщин обеднённых слоёв в р- и п- областях.

.

Вычислим полное обратное напряжение на p-n переходе, воспользовавшись тем, что в условии задачи задана максимальная величина напряжённоти электрического поля

.

Находим зарядную емкость p-n перехода на единицу площади, т.е. удельную зарядную емкость

Полная зарядная емкость p-n перехода

Задача 5.2 (для самостоятельного решения).

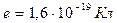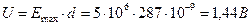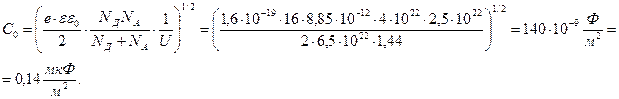
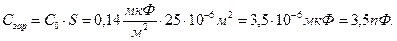
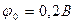Высота потенциального барьера сплавного (то есть резкого, ступенчатого) германиевого p-n перехода при тепловом равновесии . Концентрация акцепторной примеси в p- области много меньше, чем концентрация донорной примеси в n- области, она составляет 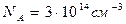. Площадь перехода 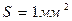. Рассчитать зарядную емкость p-n перехода, соответствующую приложенному к нему напряжению обратного смещения U при двух его значениях 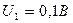и .

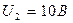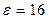При расчёте следует воспользоваться справочными данными, а именно следующими. Для германия . Электрическая постоянная вакуума , .