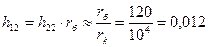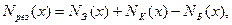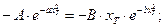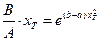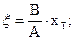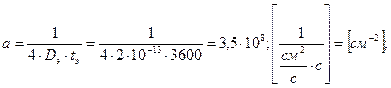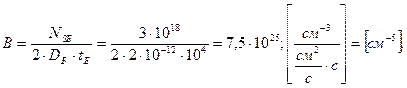Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выводы по полученным результатам.Содержание книги
Поиск на нашем сайте Проделанная работа по решению поставленных задач несомненно позволяет активизировать самостоятельную работу студентов, развивает умение выполнять информационный поиск, пользоваться справочной литературой, определять параметры и характеристики, выбирать необходимые эквивалентные схемы полупроводниковых транзисторов, даёт достаточное представление о порядке выполнения расчётов, алгоритмах их выполнения..
Задача 8.2 (для самостоятельного решения). Выбрать из справочника какой-либо биполярный транзистор (по согласованию с преподавателем) и провести для него расчёты, аналогичные представленным в настоящем разделе.
9. Расчёт h-параметров биполярного транзистора в схеме включения с общей базой . Рассмотрим эквивалентную схему биполярного транзистора с общей базой. При работе на малых сигналах транзистор удобно рассматривать как линейный активный элемент - четырехполюсник (см. рис. 9.1). Четырехполюсник характеризуется входным напряжением
Рис.9.1. Линейный активный четырехполюсник.
и напряжениями устанавливается с помощью трех систем уравнений:
Изменения этих величин связаны шестью уравнениями, которые рассмотрим попарно: первая система параметров получается из анализа уравнений (9.1):
Обозначив приращения токов
Здесь величины
называют Поэтому систему r - параметров называют системой параметров холостого хода. Так как Вторую систему параметров (9.2) можно получить из второй пары уравнений аналогично проделанному с первой парой, обозначив отношение Рассмотрим третью пару уравнений (9.3). Плоскостные транзисторы имеют следующие сопротивления: малое входное
Здесь
- входное сопротивление при коротком замыкании (КЗ) на входе;
- коэффициент передачи напряжения при XX входа;
- коэффициент передачи тока в прямом направлении при КЗ выхода;
- выходная проводимость при XX входа. Рассмотрим эквивалентную T – образную схему (рис. 9.2), элементы которой достаточно полно отражают свойства реального транзистора на низких частотах, включенного по схеме с общей базой.
Рис. 9.2. T – образная эквивалентная схема биполярного транзистора
Усилительные свойства транзистора отображены эквивалентным генератором тока где Связь h-параметров с элементами T-образной схемы. Полагая в эквивалентной схеме (см. рис. 9.2) выходное напряжение
учитывая, что
При холостом ходе на входе
Коэффициент прямой передачи тока
находим с помощью второго уравнения Кирхгофа для коллекторной цепи, полагая заданным входной ток
В этом случае можно записать
Полагая в уравнении (9.20)
Задача 9.1. Дано: Определить значения элементов на схеме (рис. 9.2). Решение. С учетом изложенного в разд., находим
Задача 9.2 (для самостоятельного решения). Дано: элементы Т – образной эквивалентной схемы биполярного транзистора: r э, r к и r б, коэффициент передачи эмиттерного тока Требуется рассчитать h – параметры. Численные значения заданных велечин по вариантам даны в табл. 9.1. Таблица 9.1 Варианты заданий к задаче 9.2.
Методические указания. Определение h – параметров возможно в следующей последовательности. Рассмотрим эту последовательность применительно к первому варианту задания.
Из выражения
Теперь определим h22 из выражения
Поскольку
Для других вариантов задания h – параметры рассчитываются аналогично.
10. Расчёт результирующего примесного распределения и точки инверсии поля в базе в структуре планарно-эпитаксиального биполярного транзистора. Результирующее примесное распределение в структуре плоскостного (планарно-эпитаксиального) биполярного транзистора (ПЭТ) представляет собой алгебраическую сумму распределений примеси в каждой из трёх областей: эмиттерной, базовой и коллекторной [1-4]. Учитывая различие в типе проводимости областей транзистора, результирующее распределение запишем в виде:
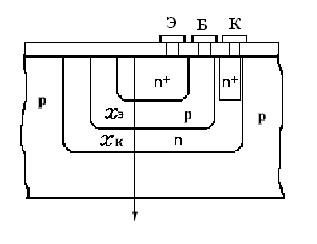
(10.1) где NЭ(x), NК(x) и NБ(x) – распределение примеси в эмиттерной, коллекторной и базовой областях, соответственно (рис.10.1). Координата x направлена вглубь полупроводниковой пластины, у поверхности x = 0.
а) б)
Рис. 10.1. Структура ПЭТ (а) и распределение концентрации легирующей примеси в структуре планарно-эпитаксиального транзистора (б).
в то время как:
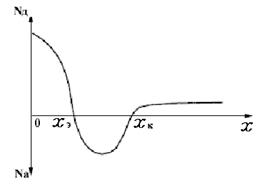
При расчёте результирующего примесного распределения NЭ(x) апроксимируется тремя erfc функциями, поскольку при высоком уровне легирования в эмиттерной области D Э является функцией концентрации донорной примеси. При этом на каждом из трёх участков эмиттерной области D Э принимается постоянным, независимым от концентрации примеси. Результирующее распределение примеси как функция от x представлено на рис. 10.2, а, б. На рис. 10.2, б распределение в базовой области представляет собой зеркальное отражение распределения на рис. 10.2, a, т.е. взято по модулю.
а) б)
доноров, Nа – концентрация акцепторов, Nрез = | Nд – Nа | - результирующая концентрация.
точке x = xт, называемой точкой инверсии. На участке xэ < x < xт поле замедляет, на участке xт < x < xк – ускоряет. Таким образом, положение точки инверсии влияет на усилительные свойства транзистора. Стремятся при проектировании сделать замедляющий участок коротким. Определяется xт из условия
(10.6)
(10.7) Распишем последовательно дифференциалы в левой и правой частях равенства (10.6):
 Обозначим: Обозначим:
Из (10.6), учитывая (10.7) – (10.8), получаем (10.9), которое перепишем в более удобном для выполнения расчётов виде
Плученное уравнение (10.10) является трансцедентным, решение данного уравнения (10.12) может быть выполнено, например, графическим путём. В результате решения данного уравнения определим значение xТ. Задача. Исходные данные: NSЭ – поверхностная концентрация области эмиттера; DЭ – коэффициент диффузии эмиттера; TЭ – время эмиттерной диффузии; xЭ – глубина эмиттера; NSБ – поверхностная концентрация базы; DБ – коэффициент диффузии базы; tБ – время диффузии базового слоя; xК – толщина коллектора. Размерности: [NSЭ], [NSБ] = см-3; [DЭ], [DБ] = см2/с; [tЭ, tБ ] = с; [xЭ, xК]= мкм. Пример решения задачи: Численные значения исходных данных: NSЭ = 1×1021 см-3; DЭ = 2×10-13 см2/с; tЭ = 3600с; xЭ = 1,5мкм; NSБ = 3×1018 см-3; DБ = 2×10-12 см2/с; tБ = 104с; xК = 3мкм; Требуется определить положение точки инверсии поля в базе биполярного транзистора xТ. Решение.
Значение xТ найдём графическим решением уравнения (10.10).
h = exp (b – a)· xT2
Для построения зависимостей x = f(xТ) и h = (xТ), составим таблицу рассчитанных значений (табл. 10.1). Вначале делаем расчет коэффициентов A, а, B и b. Затем задаёмся значениями хТ и рассчитываем значения функций x = f(xТ) и h = (xТ).:
Таблица 10.1 Зависимость значений x, h от xТ
На основании данных табл. 10.1 строим графические зависимости x(xТ) и h(xТ). Построенные зависимости представлены на рис. 10.3.
Пересечение построенных зависимостей x = f(xТ) и h = (xТ).:даёт значение xт, равное ~ 1,5мкм
Рис. 10.3. Зависимости коэффициентов x и h от xт.
Задача 10.2 (для самостоятельного решения). Заданы: NSЭ, DЭ, tЭ, xЭ, NSБ, DБ, tБ, xк. Численные значения этих параметров по вариантам даны в табл. 10.2. Требуется определить точку инверсии xТ.
Таблица 10.2 Исходные данные для решения задачи (по вариантам).
Продолжение табл. 10.2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 627; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

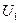 и током
и током  , а также выходным напряжением
, а также выходным напряжением 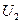 и током
и током 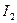 . Связь между токами
. Связь между токами
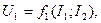
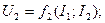 (9.1)
(9.1)
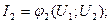 (9.2)
(9.2)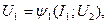
 (9.3)
(9.3)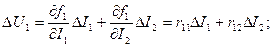 (9.4)
(9.4)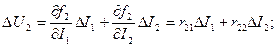 (9.5)
(9.5)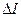 и напряжений
и напряжений 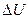 соответственно через i и u, а производные функции
соответственно через i и u, а производные функции 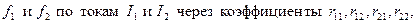 получим уравнения в виде:
получим уравнения в виде: (9.6)
(9.6)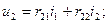 (9.7)
(9.7)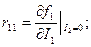

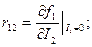
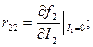 (9.8)
(9.8)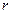 -параметрами (параметрами полных сопротивлений). Для измерения
-параметрами (параметрами полных сопротивлений). Для измерения 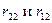 XX будет на входе, при измерении
XX будет на входе, при измерении 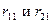 XX - на выходе.
XX - на выходе.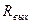 у планарных биполярных транзисторов (все выводы транзистора находятся в одной плоскости) велико, то трудно обеспечить режим XX на выходе.
у планарных биполярных транзисторов (все выводы транзистора находятся в одной плоскости) велико, то трудно обеспечить режим XX на выходе.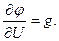 Такая система называется системой g-параметров или системой проводимостей. При определении g-параметров необходимо создавать условия короткого замыкания на выходе или входе, что трудно осуществить в реальных условиях, поскольку
Такая система называется системой g-параметров или системой проводимостей. При определении g-параметров необходимо создавать условия короткого замыкания на выходе или входе, что трудно осуществить в реальных условиях, поскольку  мало.
мало.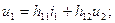 (9.9)
(9.9)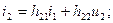 (9.10)
(9.10) (9.11)
(9.11)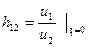 (9.12)
(9.12)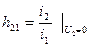 (9.13)
(9.13)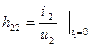 (9.14)
(9.14)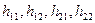 называют системой h –параметров.
называют системой h –параметров.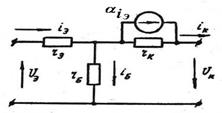
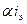 ,
, - коэффициент передачи тока транзистора (по переменному току).
- коэффициент передачи тока транзистора (по переменному току).  дифференциальные сопротивления соответственно эмиттерного и коллекторного переходов,
дифференциальные сопротивления соответственно эмиттерного и коллекторного переходов, 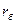 является общим для входной и выходной цепей
является общим для входной и выходной цепей и считая заданным
и считая заданным  (на входе), определим напряжение на входе:
(на входе), определим напряжение на входе: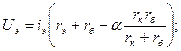 (9.15)
(9.15)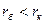 , входное сопротивление транзистора
, входное сопротивление транзистора (9.16)
(9.16)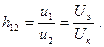 (9.17)
(9.17)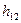 называют еще коэффициентом обратной связи по напряжению. В T - обратной схеме
называют еще коэффициентом обратной связи по напряжению. В T - обратной схеме 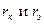
 (9.18)
(9.18)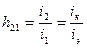 (9.19)
(9.19)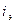
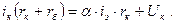 (9.20)
(9.20)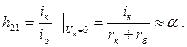 (9.21)
(9.21) , получим
, получим (9.22)
(9.22)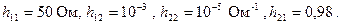
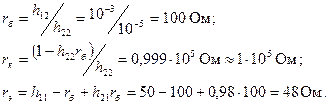
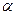 .
.

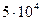
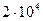

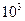


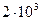
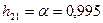 ;
;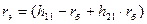 находим:
находим: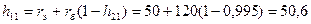 Ом.
Ом.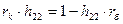
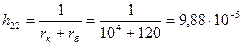 Ом
Ом 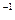 .
.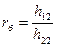 , то отсюда найдём
, то отсюда найдём