
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модифікований алгоритм симплексного пошукуСодержание книги
Поиск на нашем сайте
Розглянемо математичну постановку такої задачі: нехай потрібно відшукати локальний екстремум (мінімум) функції
При обмеженнях
визначальних припустиму область пошуку В основі базового алгоритму лежить метод комплексного пошуку /53/ з найбільш ефективними модифікаціями його, наведеними в /42/. Спочатку в припустимій області
де Відповідно до базового алгоритму /42/ на кожній ітерації комплексного пошуку заміняється “гірша” вершина комплексу. Вона відбивається через “центр ваги” інших вершин. Нехай вершини проранжировані в такий спосіб
Точка відбиття
де
Якщо
де
Уведення вершини
де
Якщо отримана точка
Якщо
Отримана на кожному з етапів припустима точка
де При багатьох гідностях наведений алгоритм має наступний принциповий недолік – мають місце випадки зациклення алгоритму. Це відбувається тоді, коли “центр ваги” комплексу Запропонована в даній роботі модифікація алгоритму комплексного пошуку полягає в тому, що в наведеному випадку повторне введення відбитої точки Дана модифікація алгоритму комплексного пошуку не тільки виключила можливість зациклення алгоритму, але й побільшала швидкість збіжності /35,96/. Це пояснюється тим, що введена операція підвищує щільність вершин комплексу в районі “кращої” вершини, що є особливо корисним на останніх ітераціях пошуку. 2.3. ДЕТЕРМІНОВАНИЙ АЛГОРИТМ БАГАТОЕКСТРЕМАЛЬНОЇ ОПТИМІЗАЦІЇ ФУНКЦІЇ, ЗАДАНОЇ НА ВІДРІЗКУ Цей і наступний параграф, відповідно до постановки задачі дослідження, даної в попередній главі, присвячені розробці й дослідженню алгоритмів багатоекстремальної оптимізації, призначених для використання в системах керування технологічними процесами. Оскільки розробка детермінованого алгоритму багатоекстремальної оптимізації, на сьогоднішній день не вирішену, то в даній роботі пропонується кілька простих алгоритмів глобального пошуку, що розвязують приватні постановки задачі (2.1), що часто зустрічаються при алгоритмізації виробничих процесів керування. Однієї з таких задач є задача багатоекстремальної оптимізації функції, заданої на відрізку. Подібно тому, як неефективно використовувати алгоритми багатоекстремальної оптимізації при відшуканні локального екстремуму функції /42/, так само ефективні алгоритми багатомірної багатоекстремальної оптимізації менш ефективні при розв'язку задач одномірної. У силу сказаного, представляється доцільної розробка спеціального алгоритму одномірної багатоекстремальної оптимізації. У даному параграфі пропонуються детермінований метод і алгоритм відшукання абсолютного мінімуму функції, заданої на відрізку, на основі комбінації методів локального пошуку й перетину паралельними площинами /49/. Розглянемо наступну постановку задачі відшукання глобального екстремуму: необхідно мінімізувати безперервну функцію
Нехай на відрізку
Ухвалюючи в якості початкової точки Покажемо, що відсутність кореня Як видне, даний алгоритм вигідно відрізняється від /49/, тим, що перетину У якості алгоритму опуклого програмування (блок4) доцільно вибрати алгоритм із високою швидкістю збіжності й не потребуючої обчислення похідних у явному виді. Таким алгоритмом може бути одномірний алгоритм Пауелла /42,43/, що володіє квадратичною збіжністю. Найбільш відповідальною й трудомісткою ланкою алгоритму є процедура знаходження кореня
У випадку, якщо дане рівняння розв'язне аналітично відносно
На жаль, у більшості випадків одержати вираження (2.23) у явному виді не вдається. Тому доводиться прибігати до чисельних методів розв'язку рівнянь /97,98/. У даному алгоритмі був застосований метод відшукання корінь довільних рівнянь Мюдлера /97,99/. З відомих методів відшукання корінь довільних рівнянь він виявляється найбільш універсальним і, як відзначається в /97/, досить надійним на практиці, хоча теоретично його збіжність у загальному випадку не доведена. Якщо мініімізуєма функція на кінцях інтервалу [a,b] свідомо вище, чим у точці абсолютного мінімуму, що належить відрізку [a,b], то від розв'язку (2.22) доцільно перейти до розв'язку нерівності
що підвищує як надійність потоку, так і його ефективність (є через число ітерацій для одержання розв'язку нерівності й те, що отримана точка, як правило, перебуває “глибше” кореня (2.22), отже краще для наступного наближення). Порівняльні характеристики даного алгоритму, як, втім, і інших багатоекстремальних алгоритмів, пропонованих у дисертації, будуть дані в наступній главі. Слід зазначити, що отриманий алгоритм ДАГП в “чисто” детермінованому виді не вдалося повідомити на багатомірний випадок. Розв'язок багатомірного рівняння (2.22) є задачею некоректної й може бути виконане аналітично лише при дуже жорстких умовах /97,100/. Розв'язок багатомірного рівняння (2.22) чисельними методами не представляється можливим, тому що вони все без винятку вимагають близької початкової точки, що в нашому випадку є метою пошуку на даному етапі (блок5). У загальному випадку розв'язок цієї задач і вдається одержати лише при використанні методу статистичних випробувань/ICI/. У якості багатомірного алгоритму опуклого програмування в блоці 4 використаний нелінійний алгоритм послідовного симплексного пошуку /43.93/, описаний 2.1 і вхідний у розроблювальний комплекс оптимізованих процедур. У комбінації ДАГП ці два методи дозволили створити досить ефективний і універсальний алгоритм глобального пошуку багатомірної функції при наявності обмежень /93,94/. Його порівняльні характеристики також будуть представлені в наступній главі.
ВИСНОВОК Програма комплексної автоматизації промисловості визначає високий темп розвитку автоматизованих систем керування технологічними процесами, технічною базою яких є мікропроцесори, міні- і спеціалізовані керуючі ЕОМ. Особливість розроблювальних систем керування полягає в тому, що незважаючи на множину різноманітних типів об'єктів керування, ці системи базуються на декількох типах керуючих обчислювальних машин у кожному з перерахованих класів. У той же час, досить поширені випадки, коли розробляється унікальне математичне забезпечення для кожного конкретного об'єкта керування. При цьому вартість математичного забезпечення часто перевищує вартість технічних засобів. Безсумнівно, що створення універсального математичного забезпечення систем керування всіма типами об'єктів не тільки малоймовірно, але й доцільно. Однак, за аналогією з технічними засобами, створення уніфікованої системи математичного забезпечення широкого класу об'єктів є розв'язною задачею. Одним зі шляхів створення уніфікованого математичного забезпечення є відомість множини задач оптимізації, що виникають на всіх стадіях алгоритмізації технологічних процесів певного класу, до декільком найбільш типовим задачам з наступною розробкою для них комплексу алгоритмів оптимізації. Дана робота присвячена питанням розробки й дослідження методів оптимізації статичних об'єктів керування, забезпечення розв'язків, що забезпечують, типових задач оптимізації, що виникають в АСУ ТП цього класу. У процесі дослідження були розглянуті й вирішені наступні задачі: 1. На основі огляду задач алгоритмізації АСУ ТП і методів оптимізації сформульована задача дослідження. Розглянуті вимоги до алгоритмів оптимізації, що працюють у рамках алгоритмізації статистичних об'єктів керування, зазначені шляхи підвищення ефективності методів локальної оптимізації й необхідність розробки методів глобальної оптимізації. 2. Розроблена модифікація алгоритму послідовного симплексного пошуку, заснована на квадратичній екстраполяції функції мети в задачах умовної оптимізації, спрямована на підвищення швидкості збіжності алгоритму. 3. Розроблена модифікація алгоритму послідовного комплексного пошуку, заснована на редукції точки відбиття, що порушувала обмеження задачі, у припустиму область у напрямку до кращої точки, спрямована на підвищення надійності й швидкості збіжності алгоритму. 4. Розроблений метод і алгоритм детермінованої багатоекстремальної оптимізації функції, заданої на відрізку, заснований на послідовній комбінації методів локальної оптимізації й пошуку кореня довільної функції, що відрізняється високою швидкістю збіжності. 5. Розроблений багатомірний інформаційно-статистичний метод і алгоритм багатоекстремального пошуку, заснований на виставі функції мети багатомірним некорельованим гаусовським випадковим процесом, що є розширенням методу інформаційно-статистичного пошуку. Алгоритм найбільш ефективний при роботі із трансцендентними функціями мети, що включають у себе синусоїди, що й мають убутний тренд у напрямку до глобального мінімуму. 6. Розроблений метод і алгоритм пошуку глобального мінімуму функції багатьох змінних, заснований на інтегральному згладжуванні функції мети, що і є найбільш ефектним при роботі з функціями, що мають обмежені втори похідні й функціональні обмеження нерівності.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ 1. Дудніков Е.Е., Цедіков Ю.М. Типові задачі оперативного керування непреривним виробництвом. – М.: Энергія, 1999.-272 с. 2. Салига В.И., Кораблев Н.М., Руденко О.Г. Автоматизованні системи керування технологічними процесами: Ідентифікація і оптимальне керування.- Харьков: Вища школа, 1989. 3. Кулик В.Т. Алгоритмізація об’єктів керування: Справочник.- Київ: Наукова думка, 1988.-362с. 4. Колін К.К., Ліпаев В.В. Проектування алгоритмів керування ЦВМ.-М.: Сов. радіо. 1990.-343с. 5. Маерс Г. Надійність програмного забезпечення. -М.: Мир,1980.-360с. 6. Растрігін Л.А., Мадшаров Н.Е. Введення в ідентифікацію об’єктов керування.-М.: Енергія, 1997.-215с. 7. Стронгін Р.Г. Монотонні алгоритми багатоекстремальної оптимізації. -В сб.: Численні методі нелінійного програмування,Харьков,1976. 8. Стронгін Р.Г. Численні методи в багатоекстремальних задачах.-М.:Наука,1998.-273с. 9. Захаров В.В. Метод інтегрального сглажування в багатоекстремальних и стохастичних задачах.- М.: Технічна кібернетика, 1980,№4. 10. Муравєв С.В., Карасташов В.А. Оптимізація модифіцированним комплексним методом Бокса.- Київ, 1982. 11. Мудров В.И. Кушко В.А. Методи обработки Измерений.-М.: Сов. Радио, 1986.-736с. 12. Авраменко В.П., Никитюк А.В. Іследованіе симплексних алгоритмів нелінійного програмування.- Харьков: Автоматизіровані системи керування і прибори автоматики, Вища школа. 13. Рубан А.И. Непараметричні процедури сглажування результатів експеримента. – М.: Системи керування,1997,№2,с.33-45. 14. Васильев Ф.П. Численні методи розв’язку екстремальних задач.- М: Наука, Главна редакція физико-математичної літератури, 1980.-520с. 15. Вершин В.Е. Автоматизовані системи керування технологічними процесами.- Л.: Машинобудування. 1993.-159с. 16. Цыпкин Я.З., Поляк Б.Т. Огрубленный метод максимального правдоподобия.- М.: Автомиатика, 1997, №12,с. 22-46 17. Попков Ю.С. и др. Ідентифікація і оптимізація нелінійних стохастичних систем.- М.: Енергія. 1995.- 440с. 18. Горский В.Г., Адлер Ю.П. Планування промислових експериментів.- М.: Металургія, 1994.- 264с. 19. Моцкус И.В. Достатні условія сходимості байесовских методів к абсолютному мінімуму непреривних функцій.- М.: Теорія оптимальних розв’язків, 1988, №4,-с.67-88. 20. Моцкус И.В. Іследованіе простого байесовского алгоритма для розв’язку багатоекстремальних задач.- Вільнюс, 1999. 21. Жилінский А.Г. Метод одномірной багатоекстремальної мінімізації.- М: Технічна кібернетика, 1986,№4,- с.71-74. 22. Эйкхофф П. Основі ідентифікації систем керування.- М.: Мир,1995.- 683с
|
||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.42.61 (0.014 с.) |


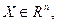 (2.12)
(2.12)




 .
. вершин. У якості первісної вершини механізмом випадкового пошуку відшукується припустима точка
вершин. У якості первісної вершини механізмом випадкового пошуку відшукується припустима точка  . Після цього інші вершини комплексу визначаються за правилом:
. Після цього інші вершини комплексу визначаються за правилом: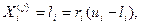
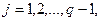
 - псевдовипадкові числа, рівномірно розподілені в інтервалі
- псевдовипадкові числа, рівномірно розподілені в інтервалі  . У процесі одержання нових вершин
. У процесі одержання нових вершин  ті точки, які порушують обмеження
ті точки, які порушують обмеження  й
й  заміняються новими, що лежать у середині відрізка, що з'єднує дану точку й “центр ваги” уже отриманих.
заміняються новими, що лежать у середині відрізка, що з'єднує дану точку й “центр ваги” уже отриманих. (2.14)
(2.14) , що заміняє “гіршу” вершину
, що заміняє “гіршу” вершину  , визначається по формулі:
, визначається по формулі: (2.15)
(2.15) - позитивний коефіцієнт відбиття
- позитивний коефіцієнт відбиття 
 - “центр ваги” комплексу
- “центр ваги” комплексу (2.16)
(2.16) то нова вершина виявляється як і раніше “гіршою” вершиною комплексу. У цьому випадку
то нова вершина виявляється як і раніше “гіршою” вершиною комплексу. У цьому випадку  (2.17)
(2.17) - коефіцієнт Хевісайда:
- коефіцієнт Хевісайда:
 :
: (2.18)
(2.18)

 :
: (2.19)
(2.19) навпіл уводиться в припустиму область
навпіл уводиться в припустиму область  (2.20)
(2.20)
 - припустима відносна точність по функції.
- припустима відносна точність по функції. (2.18). у цьому випадку введення в припустиму область
(2.18). у цьому випадку введення в припустиму область  буде не багатьом краще, чим в “гіршій” вершині комплексу
буде не багатьом краще, чим в “гіршій” вершині комплексу  . Послідовне повторення етапів уведення цієї точки в припустиму область
. Послідовне повторення етапів уведення цієї точки в припустиму область  . При цьому відбита точка зрештою обов'язково досягає певної близькості до “кращої” точки, при якій вона одночасно буде й припустимої й функція мети
. При цьому відбита точка зрештою обов'язково досягає певної близькості до “кращої” точки, при якій вона одночасно буде й припустимої й функція мети  в ній буде мати менше значення, чому в “гіршій” вершині комплексу.
в ній буде мати менше значення, чому в “гіршій” вершині комплексу. , певну на відрізку, що
, певну на відрізку, що  й має трохи локальних екстремумів
й має трохи локальних екстремумів
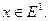 (2.21)
(2.21) локальних мінімумів з координатами
локальних мінімумів з координатами  всі
всі  й
й  - точка абсолютного мінімуму. Одним з відомих локальних методів нелінійного програмування знаходимо найближчий локальний мінімум
- точка абсолютного мінімуму. Одним з відомих локальних методів нелінійного програмування знаходимо найближчий локальний мінімум  функції
функції 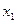 рівняння
рівняння
 в якому
в якому  процедури повторюються доти, поки в рівняння
процедури повторюються доти, поки в рівняння  не найдеться кореня
не найдеться кореня  приналежного відрізку
приналежного відрізку 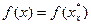 є необхідним і достатнім умовам існування в
є необхідним і достатнім умовам існування в  рівняння
рівняння  й
й  . У силу безперервності функції
. У силу безперервності функції  також безперервна й позитивно визначена в інтервалі
також безперервна й позитивно визначена в інтервалі  . З умови
. З умови  , то існує точка
, то існує точка  , досить близька до
, досить близька до  , що в обох випадках є протиріччям нашим допущенням.
, що в обох випадках є протиріччям нашим допущенням. здійснюється не навмання, а цілеспрямовано. Тому таких перетинів буде мінімальне кінцеве число й, отже, алгоритм мінімізує основні труднощі й обчислювальні витрати, пов'язані з пошуком корінь. Сам же локальний спуск при вдалому виборі одного з методів опуклого програмування не представляє скільки-небудь серйозних утруднень. Нижче на рис 2.5 представлена блок-схема алгоритму.
здійснюється не навмання, а цілеспрямовано. Тому таких перетинів буде мінімальне кінцеве число й, отже, алгоритм мінімізує основні труднощі й обчислювальні витрати, пов'язані з пошуком корінь. Сам же локальний спуск при вдалому виборі одного з методів опуклого програмування не представляє скільки-небудь серйозних утруднень. Нижче на рис 2.5 представлена блок-схема алгоритму. рівняння (блок 5)
рівняння (блок 5) (2.22)
(2.22) для певного класу функції
для певного класу функції  , те виваливши з неї
, те виваливши з неї  (2.23)
(2.23)
 (2.24)
(2.24)


