Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналіз задачі оптимізації статичних об’єктів керуванняСодержание книги
Поиск на нашем сайте
У розв'язку задачі оптимізації, як і задачі ідентифікації, історично існують два напрямки. Це так звана експериментальна оптимізація [39,40,41] і оптимізація за допомогою побудованої математичної моделі. У задачі експериментальної оптимізації, у якій функція мети задається алгоритмічно, єдино можливими для використання методами є методи прямого пошуку [39,40,41,42,43]. У задачі оптимізації за допомогою математичної моделі арсенал методів більш широкий [39,40,42,43,44]. Вибір того або іншого методу оптимізації визначається конкретною постановкою задачі. Характерними рисами задач оптимізації на етапі керування є наявність нелінійної функції мети й складної системи обмежень на керуючі параметри. Тому визначення оптимальних параметрів технологічного процесу розглянутого класу являє собою розв'язок задачі нелінійної умовної оптимізації. Відомо, що широкий клас реальних об'єктів описується квадратичною моделлю [40], в умовах якої потрібно відшукати режим, що доставляє максимум виходу при тривіальних обмеженнях на вхідні параметри. Якщо Гесіан такої моделі знаковизначен і негативний, то задача має єдиний розв'язок і його відшукання не є складним. Якщо ж Гесіан знаковизначен і позитивний, то в загальному випадку задача має множину екстремумів, розташованих на границі. Подібну ситуацію ми маємо й при відсутності знаковизначеності Гесіана, коли модель описується поверхнею типу гіперболічного параболоїда. Розглянуті ситуації характеризуються квадратичною функцією мети й тривіальною системою обмежень. Однак при наявності складної системи обмежень, що визначає неопуклу область припустимих значень, задача оптимізації в загальному випадку стає багатоекстремальної навіть при лінійній моделі. Таким чином, задача оптимізації режимів функціонування технологічних процесів у загальному виді являє собою задачу нелінійної умовної оптимізації, що часто є багатоекстремальної.
РОЗДІЛ 2
Проведений вище аналіз методів оптимізації статичних нелінійних виробничих процесів, що використовуються при алгоритмізації систем керування технологічними процесами, показав необхідність удосконалення алгоритмів симплексного й комплексного пошуку, а також розробки ефективних детермінованих процедур багатоекстремальної оптимізації на основі евристичного й статистичний^-статистичного-інформаційно-статистичного підходів. Таким чином, поставлена задача розробки комплексу алгоритмів оптимізації, що відповідають вимогам, пропонованим задачам алгоритмізації систем керування статичними нелінійними виробничими об'єктами частки, що й ефективно розвязують як, так і спільні завдання оптимізації. Сформулюємо спільну завданню оптимізації. Нехай
при обмеженнях областей, що
Оскільки алгоритм, здатний розв'язати спільне завдання оптимізації, чи навряд буде ефективний при розв'язку одноекстремальних задач /42,80/, те випливає два параграфи будуть присвячені розробці алгоритмів локальної оптимізації на основі модифікації симплексного й комплексного пошуків. Наступні параграфи, відповідно до постановки задачі дослідження, присвячуються розробці й дослідженню багатоекстремальних методів оптимізації.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 135; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.236.28 (0.009 с.) |

 - деяка довільна функція. Відзначимо, що
- деяка довільна функція. Відзначимо, що  , що доставляє глобальний мінімум функції
, що доставляє глобальний мінімум функції 
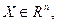 (2.1)
(2.1) визначають, пошуку:
визначають, пошуку: