
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структурний аналіз математичного забезпечення систем управління технологічними процесамиСодержание книги
Поиск на нашем сайте
У літературі [3, 5] під математичним забезпеченням систем управління технологічними процесами розуміється складання математичної моделі виробничого процесу з наступною її алгоритмізацією. Однак сьогодні це визначення не вичерпує усіх задач моделювання та алгоритмізації. Комплекс проблем математичного забезпечення систем управління технологічними процесами настільки широкий, а множина типів технологічних процесів так велика, що створення універсального математичного забезпечення для АСУ ТП представляється не тільки мало ймовірним, але й недоцільним. Однак, у рамках широких класів певних технологічних об'єктів створення для них математичного забезпечення не тільки можливе, але й з багатьох причин украй бажане. Одним з таких широких класів технологічних процесів є клас статичних технологічних процесів, які можуть бути адекватно описані наступними алгебраїчними залежностями
де Оптимальне керування цім класом об'єктів досягається шляхом мінімізації (максимізації) функції мети або критерію оптимізації
де B- вектор критерію оптимізації. Функції Основними причинами виникнення таких ситуацій є висока вартість виробництва, що не допускає проведення достатньої кількості експериментів для побудови адекватної моделі
Ця схема відбиває функціональний і інформаційний взаємозв'язок між окремими модулями системи. Незважаючи на те, що кожний модуль розробляється на окремому етапі алгоритмізації, між ними існує тісний взаємозв'язок. Тому розробку етапів алгоритмізації не можна проводити незалежно друг від друга. При цьому часто виникає необхідність внесення виправлень в алгоритми, розроблені на попередніх етапах. Однак між модулями існує не тільки інформаційний, але й змістовний взаємозв'язок, який сприяє уніфікації алгоритмів, що входять у різні модулі. Уніфікація алгоритмів, що виконують різні функції, не тільки полегшує процес проектування системи, але й сприяє розв'язку багатьох інших проблем алгоритмізації. Іншою дуже важливою властивістю системи є універсальність її використання стосовно різних об'єктів керування. Ця властивість забезпечує мінімальність необхідних змін у системі для її використання на іншому об'єкті, що має подібні характеристики (наприклад, статичність і безперервність). Обоє ці властивості системи можна досягти, визначивши загальні підходи до розв'язку найбільш важливих задач алгоритмізації. У зв'язку із цим визначимо відповідність між модулями системи алгоритмічного забезпечення (рис.1.1) і розв'язком основних задач алгоритмізації. На перших шести етапах алгоритмізації виробничого процесу розв’язується задача попередньої ідентифікації. При цьому розробляються алгоритми для блоків 3,6,7,13 і 14. Інформація про процес, яка отримується в результаті роботи алгоритмів опитування датчиків стану об'єкта (блок 13), аналізується у блоці 14. У результаті статистичного аналізу одержуємо ймовірності альтернативних гіпотез про закон розподілу перешкод на виході об'єкту. Ця інформація є вихідною для вибору критерію ідентифікації (блок 3). У блоці 7 сформована математична модель об'єкта. Інформація блоків 3 і 7 є вихідною для розв'язку задачі оцінювання параметрів математичної моделі технологічного процесу (блок 6). У результаті роботи блоків 3,6 і 7виходить математична модель об'єкта, адекватна в сенсі прийнятого критерію ідентифікації. Однак, ця модель є першим наближенням і згодом підлягає періодичному уточненню. З цією метою розробляються алгоритми для блоків 9 і 11, які розв’язують задачу планування активного експерименту. Вихідною інформацією для цього є модель технологічного процесу, що отримана на попередніх етапах. Блок 9 виробляє план активного експерименту
|
||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 124; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.189.236 (0.007 с.) |

 :
:
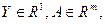


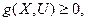


 - вихідний параметр об'єктів керування,
- вихідний параметр об'єктів керування, 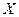 - вектор вихідних параметрів,
- вектор вихідних параметрів, 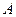 - вектор коефіцієнтів,
- вектор коефіцієнтів,  - вектор параметрів керування,
- вектор параметрів керування,  -перешкода на виході об'єкта керування,
-перешкода на виході об'єкта керування,  - функції обмеження,
- функції обмеження,  ,
, 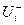 - нижні й верхні границі параметрів керування.
- нижні й верхні границі параметрів керування.
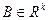
 й
й  у загальному випадку можуть бути нелінійними, розривними й багатоекстремальними. Тоді задача визначення оптимального керування
у загальному випадку можуть бути нелінійними, розривними й багатоекстремальними. Тоді задача визначення оптимального керування  буде задачею нелінійного програмування й може бути розв’язана за допомогою методів нелінійної або багатоекстремальної оптимізації. Однак більшість виробничих об'єктів згодом міняють свої характеристики, що вимагає періодичного підстроювання коефіцієнтів моделі й коефіцієнтів критерію
буде задачею нелінійного програмування й може бути розв’язана за допомогою методів нелінійної або багатоекстремальної оптимізації. Однак більшість виробничих об'єктів згодом міняють свої характеристики, що вимагає періодичного підстроювання коефіцієнтів моделі й коефіцієнтів критерію  , отже, і оптимального керування
, отже, і оптимального керування  - невідома й оптимальне керування
- невідома й оптимальне керування 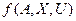 , або така нестаціонарність об'єктів керування, яка не дозволяє ефективно стежити за параметрами моделі об'єкта й коефіцієнтами
, або така нестаціонарність об'єктів керування, яка не дозволяє ефективно стежити за параметрами моделі об'єкта й коефіцієнтами 
 . Цей план надходить у блок керування додатковими обладнаннями (блок 11). Алгоритми блоку 11 виробляють керуючий вплив
. Цей план надходить у блок керування додатковими обладнаннями (блок 11). Алгоритми блоку 11 виробляють керуючий вплив  на виконавчі обладнання (блок 16). Виконавчі обладнання забезпечують задані блоком 9 вхідні параметри технологічного процесу
на виконавчі обладнання (блок 16). Виконавчі обладнання забезпечують задані блоком 9 вхідні параметри технологічного процесу 


