Модифікація алгоритму послідовного
СИМПЛЕКСНОГО ПОШУКУ
У справжньому параграфі розглянута вище постановка загальної задачі оптимізації (2.1) обмежується вимогам відшукання локального екстремуму функції 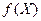 в області в області  . Порівняльний аналіз ефективності роботи різних процедур симплексного пошуку /42,91,92/ показав, що найбільш ефективною процедурою є алгоритм Нелдера-Міда в комбінації з методом ковзного допуску /43/, який надалі буде використовуватися в якості базового. Даний алгоритм полягає в організації в області пошуку . Порівняльний аналіз ефективності роботи різних процедур симплексного пошуку /42,91,92/ показав, що найбільш ефективною процедурою є алгоритм Нелдера-Міда в комбінації з методом ковзного допуску /43/, який надалі буде використовуватися в якості базового. Даний алгоритм полягає в організації в області пошуку   - верхового - верхового 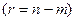 правильного багатогранника (симплекса) з довгої ребра правильного багатогранника (симплекса) з довгої ребра  і його руху в антиградієнтом напрямку, не виходячи за межі і його руху в антиградієнтом напрямку, не виходячи за межі  , за допомогою операцій відбиття, наближення, розтягання, стиску й редукції. Усі операції, за винятком редукції, проводяться в напрямку напівпрямої, що проходить від “гіршої” вершини симплекса через центр (“ваги”) протилежної до неї грані. Отримана в результаті операцій точка заміняє “гіршу” вершину симплекса. Гнучка організація руху симплекса дозволяє йому успішно долати “яри”, “хребти” і сідлові точки на поверхні функції мети. Однак, швидкість просування симплекса в антиградієнтом напрямку може бути суттєво збільшена за рахунок проведення операцій відбиття й розтягання не через центр протилежної до “гіршої” вершини грані, а ближче до напрямку дійсного антиградієнта. Цього можна досягти, завдяки оцінці градієнта гіперплощини, що проходить через вершини симплекса /40,46/ або застосовуючи рекомендації Умеда-Ічикави по обчисленню зваженого “центру ваги” /40,42,54/. Іншою модифікацією базового алгоритму, спрямованої на істотне підвищення швидкості пошуку екстремуму, є застосування квадратичної екстраполяції функції мети в напрямку вдалого розтягання й оцінки по екстраполюючій параболі мінімуму , за допомогою операцій відбиття, наближення, розтягання, стиску й редукції. Усі операції, за винятком редукції, проводяться в напрямку напівпрямої, що проходить від “гіршої” вершини симплекса через центр (“ваги”) протилежної до неї грані. Отримана в результаті операцій точка заміняє “гіршу” вершину симплекса. Гнучка організація руху симплекса дозволяє йому успішно долати “яри”, “хребти” і сідлові точки на поверхні функції мети. Однак, швидкість просування симплекса в антиградієнтом напрямку може бути суттєво збільшена за рахунок проведення операцій відбиття й розтягання не через центр протилежної до “гіршої” вершини грані, а ближче до напрямку дійсного антиградієнта. Цього можна досягти, завдяки оцінці градієнта гіперплощини, що проходить через вершини симплекса /40,46/ або застосовуючи рекомендації Умеда-Ічикави по обчисленню зваженого “центру ваги” /40,42,54/. Іншою модифікацією базового алгоритму, спрямованої на істотне підвищення швидкості пошуку екстремуму, є застосування квадратичної екстраполяції функції мети в напрямку вдалого розтягання й оцінки по екстраполюючій параболі мінімуму 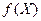 /42/. Нижче пропонується модифікований алгоритм симплексного пошуку, що володіє підвищеною швидкістю пошуку екстремуму функції декількох змінних при наявності обмежень. Причому, квадратична екстраполяція функції мети в даній модифікації проводиться з урахуванням можливості порушення обмежень задачі на операціях відбиття й розтягання /93,94/. /42/. Нижче пропонується модифікований алгоритм симплексного пошуку, що володіє підвищеною швидкістю пошуку екстремуму функції декількох змінних при наявності обмежень. Причому, квадратична екстраполяція функції мети в даній модифікації проводиться з урахуванням можливості порушення обмежень задачі на операціях відбиття й розтягання /93,94/.
У припустимій області  згідно з рекомендаціями /43/ будується вихідний симплекс із згідно з рекомендаціями /43/ будується вихідний симплекс із  -ою вершиною й довжиною ребра -ою вершиною й довжиною ребра  . Нехай в “найгіршій” вершині симплекса . Нехай в “найгіршій” вершині симплекса  функція мети функція мети  ,а в найкращій вершині ,а в найкращій вершині   . Розрахунки завершеного “центру ваги” . Розрахунки завершеного “центру ваги”  протилежної до протилежної до  грані симплекса проводиться згідно /54/ грані симплекса проводиться згідно /54/
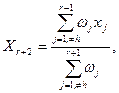 (2.2) (2.2)
де  - ваги - ваги  вершин симплекса, вершин симплекса,  - число незалежних змінних задачі (2.1). - число незалежних змінних задачі (2.1).
Зважений “центр ваги” дозволяє симплексу рухатися в напрямку, більш близькому до напрямку антиградієнта.
Операція відбиття “найгіршої” точки  через “центр ваги” симплекса через “центр ваги” симплекса  проводиться згідно з вираженням проводиться згідно з вираженням
 (2.3) (2.3)
де  - координати точки відбиття, а - координати точки відбиття, а  - коефіцієнт відбиття - коефіцієнт відбиття  . Отримана точка . Отримана точка  відповідно до методу ковзного допуску /43/ перевіряється на допустимість і якщо потрібно, то переводиться в припустиму область відповідно до методу ковзного допуску /43/ перевіряється на допустимість і якщо потрібно, то переводиться в припустиму область  (2.1). У методі ковзного допуску в досліджуваній точці перевіряється нерівність (2.1). У методі ковзного допуску в досліджуваній точці перевіряється нерівність
 (2.4) (2.4)
де  - значення критерію ковзного допуску, обумовлене як - значення критерію ковзного допуску, обумовлене як


 - довга ребра вихідного симплекса, - довга ребра вихідного симплекса,  - номер ітерації, - номер ітерації, 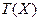 - функціонал над множиною обмежень вид, що має: - функціонал над множиною обмежень вид, що має:
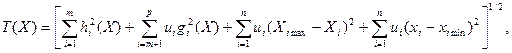
 -функція Хевисайда: -функція Хевисайда:
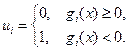
Якщо нерівність не виконується, то досліджувана точка X переводиться в припустиму область D шляхом мінімізації функціонала T(X) у простір  . Мінімізація T(X) може проводиться тим же алгоритмом послідовного симплексного пошуку. . Мінімізація T(X) може проводиться тим же алгоритмом послідовного симплексного пошуку.
Після введення  в припустиму область в припустиму область 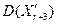 визначається значення функції в ній визначається значення функції в ній 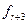 і рівняється зі значеннями функції у вершинах симплекса. Якщо і рівняється зі значеннями функції у вершинах симплекса. Якщо  , то виконується операція розтягання , то виконується операція розтягання

де  -коефіцієнт розтягання -коефіцієнт розтягання 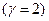 . .
У точці 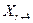 перевіряється нерівність (2.4) і у випадку його виконання точка розтягання вводиться в припустиму область - перевіряється нерівність (2.4) і у випадку його виконання точка розтягання вводиться в припустиму область - 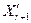 . Якщо . Якщо  , то з метою підвищення швидкості пошуку проводиться квадратична екстраполяція , то з метою підвищення швидкості пошуку проводиться квадратична екстраполяція 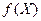 по напрямкові напівпрямої, що проходить через точки по напрямкові напівпрямої, що проходить через точки 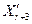 й й 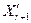 . А якщо ні, то, “гірша” вершина заміняється на відбиту . А якщо ні, то, “гірша” вершина заміняється на відбиту 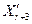 . .
Пропонована модифікація алгоритму, у відмінності від наведеної в /42/, пропонує проведення екстраполяції функції мети не по напрямкові напівпрямої, що проходить через  і і 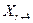 , а по напрямкові напівпрямої, що проходить через , а по напрямкові напівпрямої, що проходить через 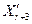 і і 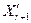 , уже введених у припустиму область D. Оскільки операція розтягання суттєво видаляє точку , уже введених у припустиму область D. Оскільки операція розтягання суттєво видаляє точку 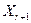 від “центру ваги” симплекса від “центру ваги” симплекса 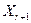 , то при цьому досить часті випадки порушення в ній обмежень задачі (2.1). І тому що після проведених крапок відбиття й розтягання в припустиму область D ці точки їжаку не лежать на одній прямій з “гіршою” крапкою симплекса , то при цьому досить часті випадки порушення в ній обмежень задачі (2.1). І тому що після проведених крапок відбиття й розтягання в припустиму область D ці точки їжаку не лежать на одній прямій з “гіршою” крапкою симплекса  , то провести екстраполяцію, як пропонується в /42/, не представляється можливим. Нижче пропонується процедура екстраполяції функції мети, що враховує можливість порушення обмежень задачі в процесі пошуку , то провести екстраполяцію, як пропонується в /42/, не представляється можливим. Нижче пропонується процедура екстраполяції функції мети, що враховує можливість порушення обмежень задачі в процесі пошуку
Квадратична екстраполяція функції мети по напрямкові здійснюється по трьом точкам: 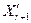 - уведеної в область D точки розтягання - уведеної в область D точки розтягання 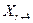 , , 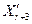 - уведеної в області D точки відбиття - уведеної в області D точки відбиття  й й 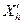 - проекції “гіршої” точки - проекції “гіршої” точки  на пряму H, що проходить через точки на пряму H, що проходить через точки 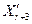 й й  . Перед екстраполяцією необхідно визначити проекцію . Перед екстраполяцією необхідно визначити проекцію  на на 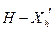 й значення функції в ній й значення функції в ній 
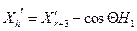 , ,
де   (2.6) (2.6)
  , , 
Відносна точка мінімуму екстраполюючої параболи  , що перебуває на прямій H із крапкою відліку в , що перебуває на прямій H із крапкою відліку в 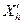 , визначається вираженням , визначається вираженням
 (2.7) (2.7)
де  . .
Точка мінімуму екстраполюючої параболи в просторі
 (2.8) (2.8)
Перевіряється на приналежність припустимої області D і якщо необхідно, те вводиться в припустиму область. У припустимій точці  визначається значення функції мети визначається значення функції мети  , яке потім рівняється с. , яке потім рівняється с.  Якщо Якщо 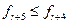 , то , то  заміняється на заміняється на  . А якщо ні, то . А якщо ні, то  заміняється на заміняється на 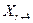 . В іншому алгоритм відповідає наведеному в /43/. Якщо . В іншому алгоритм відповідає наведеному в /43/. Якщо  , де , де  , , 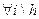 , то відбиття також зізнається вдалим і припустима відбита точка , то відбиття також зізнається вдалим і припустима відбита точка 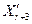 заміняє “гіршу” вершину симплекса заміняє “гіршу” вершину симплекса  . Якщо . Якщо  , то проводиться наближення відбитої точки , то проводиться наближення відбитої точки
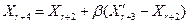 , (2.9) , (2.9)
Де 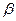 - коефіцієнт стиску - коефіцієнт стиску  ; якщо ; якщо  , те виконується операція стиску , те виконується операція стиску
 (2.10) (2.10)
Отримана точка 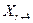 вводиться в припустиму область вводиться в припустиму область 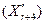 і в ній визначається значення функції мети і в ній визначається значення функції мети  . Якщо . Якщо  то виконується операція редукції симплекса до кращої точки то виконується операція редукції симплекса до кращої точки
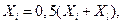  (2.11) (2.11)
Розглянутий алгоритм послідовного симплексного пошуку є досить універсальною процедурою оптимізації. Він може використовуватися при експериментальній оптимізації виробничих процесів без попередньої побудови їх моделей і ефективний при розв'язку задач оптимізації з обмеженнями типу рівностей. Однак у більш приватних задач оптимізації, що не мають обмежень – рівностей, комплексний пошук Боксу /53/ має більшу швидкість збіжності /42/. Наступний параграф присвячений розгляду алгоритму комплексного пошуку й розробці його модифікації, що підвищує його надійність.
|



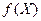 в області
в області  . Порівняльний аналіз ефективності роботи різних процедур симплексного пошуку /42,91,92/ показав, що найбільш ефективною процедурою є алгоритм Нелдера-Міда в комбінації з методом ковзного допуску /43/, який надалі буде використовуватися в якості базового. Даний алгоритм полягає в організації в області пошуку
. Порівняльний аналіз ефективності роботи різних процедур симплексного пошуку /42,91,92/ показав, що найбільш ефективною процедурою є алгоритм Нелдера-Міда в комбінації з методом ковзного допуску /43/, який надалі буде використовуватися в якості базового. Даний алгоритм полягає в організації в області пошуку  - верхового
- верхового 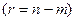 правильного багатогранника (симплекса) з довгої ребра
правильного багатогранника (симплекса) з довгої ребра  і його руху в антиградієнтом напрямку, не виходячи за межі
і його руху в антиградієнтом напрямку, не виходячи за межі  -ою вершиною й довжиною ребра
-ою вершиною й довжиною ребра  функція мети
функція мети  ,а в найкращій вершині
,а в найкращій вершині 
 . Розрахунки завершеного “центру ваги”
. Розрахунки завершеного “центру ваги”  протилежної до
протилежної до 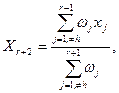 (2.2)
(2.2) - ваги
- ваги  вершин симплекса,
вершин симплекса,  - число незалежних змінних задачі (2.1).
- число незалежних змінних задачі (2.1). (2.3)
(2.3) - координати точки відбиття, а
- координати точки відбиття, а  - коефіцієнт відбиття
- коефіцієнт відбиття  . Отримана точка
. Отримана точка  (2.4)
(2.4) - значення критерію ковзного допуску, обумовлене як
- значення критерію ковзного допуску, обумовлене як

 - номер ітерації,
- номер ітерації, 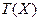 - функціонал над множиною обмежень вид, що має:
- функціонал над множиною обмежень вид, що має: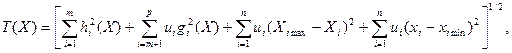
 -функція Хевисайда:
-функція Хевисайда: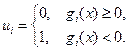
 . Мінімізація T(X) може проводиться тим же алгоритмом послідовного симплексного пошуку.
. Мінімізація T(X) може проводиться тим же алгоритмом послідовного симплексного пошуку. в припустиму область
в припустиму область 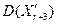 визначається значення функції в ній
визначається значення функції в ній 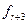 і рівняється зі значеннями функції у вершинах симплекса. Якщо
і рівняється зі значеннями функції у вершинах симплекса. Якщо  , то виконується операція розтягання
, то виконується операція розтягання
 -коефіцієнт розтягання
-коефіцієнт розтягання 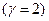 .
.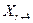 перевіряється нерівність (2.4) і у випадку його виконання точка розтягання вводиться в припустиму область -
перевіряється нерівність (2.4) і у випадку його виконання точка розтягання вводиться в припустиму область - 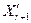 . Якщо
. Якщо  , то з метою підвищення швидкості пошуку проводиться квадратична екстраполяція
, то з метою підвищення швидкості пошуку проводиться квадратична екстраполяція 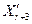 й
й  і
і 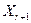 від “центру ваги” симплекса
від “центру ваги” симплекса  , то провести екстраполяцію, як пропонується в /42/, не представляється можливим. Нижче пропонується процедура екстраполяції функції мети, що враховує можливість порушення обмежень задачі в процесі пошуку
, то провести екстраполяцію, як пропонується в /42/, не представляється можливим. Нижче пропонується процедура екстраполяції функції мети, що враховує можливість порушення обмежень задачі в процесі пошуку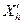 - проекції “гіршої” точки
- проекції “гіршої” точки  . Перед екстраполяцією необхідно визначити проекцію
. Перед екстраполяцією необхідно визначити проекцію 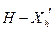 й значення функції в ній
й значення функції в ній 
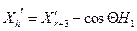 ,
,
 (2.6)
(2.6)
 ,
, 
 , що перебуває на прямій H із крапкою відліку в
, що перебуває на прямій H із крапкою відліку в  (2.7)
(2.7) .
. (2.8)
(2.8) визначається значення функції мети
визначається значення функції мети  , яке потім рівняється с.
, яке потім рівняється с.  Якщо
Якщо 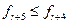 , то
, то  . А якщо ні, то
. А якщо ні, то  , де
, де  ,
, 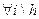 , то відбиття також зізнається вдалим і припустима відбита точка
, то відбиття також зізнається вдалим і припустима відбита точка  , то проводиться наближення відбитої точки
, то проводиться наближення відбитої точки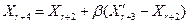 , (2.9)
, (2.9)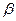 - коефіцієнт стиску
- коефіцієнт стиску  ; якщо
; якщо  , те виконується операція стиску
, те виконується операція стиску (2.10)
(2.10)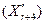 і в ній визначається значення функції мети
і в ній визначається значення функції мети  то виконується операція редукції симплекса до кращої точки
то виконується операція редукції симплекса до кращої точки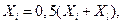
 (2.11)
(2.11)


