
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
МІнІстерство освіти і науки, молоді та спорту УкраїниСодержание книги
Поиск на нашем сайте
МІнІстерство освіти і науки, молоді та спорту України СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ Імені ВОЛОДИМИРА ДАЛЯ
Кафедра прикладної математики
Звіт з преддипломної практики
Робота захищена з оцінкою ________________________
Луганськ - 2012
Зміст ВВЕДЕННЯ- 4 РОЗДІЛ 1 Аналіз сучасного стану проблемИ синтезу систем управління технологічними процесами- 6 1.1. Структурний аналіз математичного забезпечення систем управління технологічними процесами- 7 1.2. Аналіз задачі ідентифікації об’єктів керування технологічними процесами 12 1.3. Аналіз задачі планування активних експериментів- 15 1.4. Аналіз задачі оптимізації статичних об’єктів керування- 16 РОЗДІЛ 2 РОЗРОБКА Й ДОСЛІДЖЕННЯ АЛГОРИТМІВ ОПТИМІЗАЦІЇ ВИРОБНИЧИХ ПРОЦЕСІВ- 17 2.1.МОДИФІКАЦІЯ АЛГОРИТМУ ПОСЛІДОВНОГО-- 18 СИМПЛЕКСНОГО ПОШУКУ- 18 2.2.МОДИФІКАЦІЯ АЛГОРИТМУ КОМПЛЕКСНОГО ПОШУКУ- 22 2.3. ДЕТЕРМІНОВАНИЙ АЛГОРИТМ БАГАТОЕКСТРЕМАЛЬНОЇ ОПТИМІЗАЦІЇ ФУНКЦІЇ, ЗАДАНОЇ НА ВІДРІЗКУ- 27 ВИСНОВОК- 31 СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ- 33
В основних напрямках економічного й соціального розвитку України на період до 2020 року одним з основних шляхів підвищення ефективності суспільного виробництва вказується на необхідність інтенсивного впровадження комплексної механізації й автоматизації виробничих процесів. У цьому зв'язку найважливішою науково-технічною задачею є забезпечення виробництва системами автоматичного керування з використанням мікропроцесорів. У рамках цієї задачі удосконалювання обчислювальної техніки, її елементної бази й математичного забезпечення, засобів і систем збору, передачі й обробки інформації є найважливішою проблемою природніх і технічних наук. Створенню ефективних систем керування технологічними процесами передує більша робота по експериментальному дослідженню й алгоритмізації технологічних процесів, що включає в себе методи і синтез алгоритмів статистичного аналізу, планування активних експериментів, ідентифікації, прогнозування й оптимізації. Причому, в основі більшості методів на різних етапах алгоритмізації лежить розв'язок багатоекстремальних задач оптимізації з відповідними критеріями. Тому проблеми оптимізації є ключовими при синтезі кожної конкретної системи керування технологічним процесом. Технічною базою систем керування є мікропроцесори та обчислювальні машини, що управляють, електронні обладнання регулювання й телемеханіки, виконавчі механізми, прилади й датчики систем комплексної автоматизації технологічних процесів. Однак самі по собі технічні засоби не розв’язують проблем керування. Тому не менш важливим компонентом проектування керуючих систем комплексної автоматизації технологічних процесів є математичне й програмне забезпечення керуючих обчислювальних засобів. Технічні особливості керуючих обчислювальних комплексів, а також особливості функціонування керуючих систем у реальному масштабі часу пред'являють до програм математичного забезпечення певні вимоги. У рамках даної дипломної роботи поставлена й розв’язується задача розробки комплексу алгоритмів оптимізації в задачах алгоритмізації процесів керування технологічними об'єктам. До складу комплексу включені детерміновані алгоритми локальної й багатоекстремальної оптимізації, що задовольняють вимогам алгоритмізації й розв’язують широкий клас задач на всіх етапах проектування й експлуатації системи керування. Запропоновані модифікації нелінійних симплекс - методів, спрямованих на збільшення їх швидкості збіжності й підвищення надійності пошуку при роботі зі складними обмеженнями. Розглянута група алгоритмів багатоекстремального пошуку, що дозволяють розв’язувати найпоширеніші задачі багатоекстремальної оптимізації, які виникають при проектуванні й експлуатації комплексних систем керування технологічними об'єктами. Результати аналізу послужили рекомендацією із практичного використання алгоритмів розглянутого класу. РОЗДІЛ 1
Однієї з найважливіших проблем проектування систем керування технологічними процесами є алгоритмізація процесів керування, тобто розробка зовнішнього математичного забезпечення керуючих обчислювальних машин [2, 3, 4]. Теорія алгоритмізації процесів керування виробничими об'єктами з'явилася в той момент, коли розвиток обчислювальної техніки дозволив залучати її до розв'язку складних виробничих задач. Особливості задач керування виробництвом викликали необхідність створення спеціалізованих керуючих машин або процесорів. Їх конструктивними особливостями є підвищена надійність роботи, висока швидкодія та малий об'єм оперативної пам’яті. Вони накладають на програмне забезпечення керуючих обчислювальних машин такі вимоги як: мінімальність розміру програмних модулів, мала їхня чутливість до точності обчислювальних операцій, програмна керованість часом розв'язку задач і ряд інших, що залежать від особливостей функціонального призначення системи керування Алгоритми ідентифікації й керування технологічними процесами часто ґрунтуються на методах в обчислювальному відношенні потребуючих більших об'ємів оперативної пам'яті, високої кваліфікації користувачів, тривалої підготовки до розв’язку й таке інше. Програмування таких алгоритмів для спеціалізованих керуючих машин сполучене з більшими труднощами й спричиняє втрату ефективності керуючих програм [7, 8]. Усе більш наполегливо проявляється тенденція використання спеціалізованих керуючих обчислювальних машин для розв'язку задач оптимізації процесів виробництва, пред'являє ряд вимог до їх математичного забезпечення. Аналіз методів алгоритмізації процесів виробництва у світлі цих вимог і постановка задачі дослідження становлять основний зміст даного розділу.
СИМПЛЕКСНОГО ПОШУКУ У справжньому параграфі розглянута вище постановка загальної задачі оптимізації (2.1) обмежується вимогам відшукання локального екстремуму функції У припустимій області
де Зважений “центр ваги” дозволяє симплексу рухатися в напрямку, більш близькому до напрямку антиградієнта. Операція відбиття “найгіршої” точки
де
де
Якщо нерівність не виконується, то досліджувана точка X переводиться в припустиму область D шляхом мінімізації функціонала T(X) у простір Після введення
де У точці Пропонована модифікація алгоритму, у відмінності від наведеної в /42/, пропонує проведення екстраполяції функції мети не по напрямкові напівпрямої, що проходить через Квадратична екстраполяція функції мети по напрямкові здійснюється по трьом точкам:
де
Відносна точка мінімуму екстраполюючої параболи
де Точка мінімуму екстраполюючої параболи в просторі
Перевіряється на приналежність припустимої області D і якщо необхідно, те вводиться в припустиму область. У припустимій точці
Де
Отримана точка
Розглянутий алгоритм послідовного симплексного пошуку є досить універсальною процедурою оптимізації. Він може використовуватися при експериментальній оптимізації виробничих процесів без попередньої побудови їх моделей і ефективний при розв'язку задач оптимізації з обмеженнями типу рівностей. Однак у більш приватних задач оптимізації, що не мають обмежень – рівностей, комплексний пошук Боксу /53/ має більшу швидкість збіжності /42/. Наступний параграф присвячений розгляду алгоритму комплексного пошуку й розробці його модифікації, що підвищує його надійність. ВИСНОВОК Програма комплексної автоматизації промисловості визначає високий темп розвитку автоматизованих систем керування технологічними процесами, технічною базою яких є мікропроцесори, міні- і спеціалізовані керуючі ЕОМ. Особливість розроблювальних систем керування полягає в тому, що незважаючи на множину різноманітних типів об'єктів керування, ці системи базуються на декількох типах керуючих обчислювальних машин у кожному з перерахованих класів. У той же час, досить поширені випадки, коли розробляється унікальне математичне забезпечення для кожного конкретного об'єкта керування. При цьому вартість математичного забезпечення часто перевищує вартість технічних засобів. Безсумнівно, що створення універсального математичного забезпечення систем керування всіма типами об'єктів не тільки малоймовірно, але й доцільно. Однак, за аналогією з технічними засобами, створення уніфікованої системи математичного забезпечення широкого класу об'єктів є розв'язною задачею. Одним зі шляхів створення уніфікованого математичного забезпечення є відомість множини задач оптимізації, що виникають на всіх стадіях алгоритмізації технологічних процесів певного класу, до декільком найбільш типовим задачам з наступною розробкою для них комплексу алгоритмів оптимізації. Дана робота присвячена питанням розробки й дослідження методів оптимізації статичних об'єктів керування, забезпечення розв'язків, що забезпечують, типових задач оптимізації, що виникають в АСУ ТП цього класу. У процесі дослідження були розглянуті й вирішені наступні задачі: 1. На основі огляду задач алгоритмізації АСУ ТП і методів оптимізації сформульована задача дослідження. Розглянуті вимоги до алгоритмів оптимізації, що працюють у рамках алгоритмізації статистичних об'єктів керування, зазначені шляхи підвищення ефективності методів локальної оптимізації й необхідність розробки методів глобальної оптимізації. 2. Розроблена модифікація алгоритму послідовного симплексного пошуку, заснована на квадратичній екстраполяції функції мети в задачах умовної оптимізації, спрямована на підвищення швидкості збіжності алгоритму. 3. Розроблена модифікація алгоритму послідовного комплексного пошуку, заснована на редукції точки відбиття, що порушувала обмеження задачі, у припустиму область у напрямку до кращої точки, спрямована на підвищення надійності й швидкості збіжності алгоритму. 4. Розроблений метод і алгоритм детермінованої багатоекстремальної оптимізації функції, заданої на відрізку, заснований на послідовній комбінації методів локальної оптимізації й пошуку кореня довільної функції, що відрізняється високою швидкістю збіжності. 5. Розроблений багатомірний інформаційно-статистичний метод і алгоритм багатоекстремального пошуку, заснований на виставі функції мети багатомірним некорельованим гаусовським випадковим процесом, що є розширенням методу інформаційно-статистичного пошуку. Алгоритм найбільш ефективний при роботі із трансцендентними функціями мети, що включають у себе синусоїди, що й мають убутний тренд у напрямку до глобального мінімуму. 6. Розроблений метод і алгоритм пошуку глобального мінімуму функції багатьох змінних, заснований на інтегральному згладжуванні функції мети, що і є найбільш ефектним при роботі з функціями, що мають обмежені втори похідні й функціональні обмеження нерівності.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ 1. Дудніков Е.Е., Цедіков Ю.М. Типові задачі оперативного керування непреривним виробництвом. – М.: Энергія, 1999.-272 с. 2. Салига В.И., Кораблев Н.М., Руденко О.Г. Автоматизованні системи керування технологічними процесами: Ідентифікація і оптимальне керування.- Харьков: Вища школа, 1989. 3. Кулик В.Т. Алгоритмізація об’єктів керування: Справочник.- Київ: Наукова думка, 1988.-362с. 4. Колін К.К., Ліпаев В.В. Проектування алгоритмів керування ЦВМ.-М.: Сов. радіо. 1990.-343с. 5. Маерс Г. Надійність програмного забезпечення. -М.: Мир,1980.-360с. 6. Растрігін Л.А., Мадшаров Н.Е. Введення в ідентифікацію об’єктов керування.-М.: Енергія, 1997.-215с. 7. Стронгін Р.Г. Монотонні алгоритми багатоекстремальної оптимізації. -В сб.: Численні методі нелінійного програмування,Харьков,1976. 8. Стронгін Р.Г. Численні методи в багатоекстремальних задачах.-М.:Наука,1998.-273с. 9. Захаров В.В. Метод інтегрального сглажування в багатоекстремальних и стохастичних задачах.- М.: Технічна кібернетика, 1980,№4. 10. Муравєв С.В., Карасташов В.А. Оптимізація модифіцированним комплексним методом Бокса.- Київ, 1982. 11. Мудров В.И. Кушко В.А. Методи обработки Измерений.-М.: Сов. Радио, 1986.-736с. 12. Авраменко В.П., Никитюк А.В. Іследованіе симплексних алгоритмів нелінійного програмування.- Харьков: Автоматизіровані системи керування і прибори автоматики, Вища школа. 13. Рубан А.И. Непараметричні процедури сглажування результатів експеримента. – М.: Системи керування,1997,№2,с.33-45. 14. Васильев Ф.П. Численні методи розв’язку екстремальних задач.- М: Наука, Главна редакція физико-математичної літератури, 1980.-520с. 15. Вершин В.Е. Автоматизовані системи керування технологічними процесами.- Л.: Машинобудування. 1993.-159с. 16. Цыпкин Я.З., Поляк Б.Т. Огрубленный метод максимального правдоподобия.- М.: Автомиатика, 1997, №12,с. 22-46 17. Попков Ю.С. и др. Ідентифікація і оптимізація нелінійних стохастичних систем.- М.: Енергія. 1995.- 440с. 18. Горский В.Г., Адлер Ю.П. Планування промислових експериментів.- М.: Металургія, 1994.- 264с. 19. Моцкус И.В. Достатні условія сходимості байесовских методів к абсолютному мінімуму непреривних функцій.- М.: Теорія оптимальних розв’язків, 1988, №4,-с.67-88. 20. Моцкус И.В. Іследованіе простого байесовского алгоритма для розв’язку багатоекстремальних задач.- Вільнюс, 1999. 21. Жилінский А.Г. Метод одномірной багатоекстремальної мінімізації.- М: Технічна кібернетика, 1986,№4,- с.71-74. 22. Эйкхофф П. Основі ідентифікації систем керування.- М.: Мир,1995.- 683с
МІнІстерство освіти і науки, молоді та спорту України
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.21.106 (0.009 с.) |

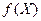 в області
в області  . Порівняльний аналіз ефективності роботи різних процедур симплексного пошуку /42,91,92/ показав, що найбільш ефективною процедурою є алгоритм Нелдера-Міда в комбінації з методом ковзного допуску /43/, який надалі буде використовуватися в якості базового. Даний алгоритм полягає в організації в області пошуку
. Порівняльний аналіз ефективності роботи різних процедур симплексного пошуку /42,91,92/ показав, що найбільш ефективною процедурою є алгоритм Нелдера-Міда в комбінації з методом ковзного допуску /43/, який надалі буде використовуватися в якості базового. Даний алгоритм полягає в організації в області пошуку  - верхового
- верхового 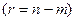 правильного багатогранника (симплекса) з довгої ребра
правильного багатогранника (симплекса) з довгої ребра  і його руху в антиградієнтом напрямку, не виходячи за межі
і його руху в антиградієнтом напрямку, не виходячи за межі  -ою вершиною й довжиною ребра
-ою вершиною й довжиною ребра  функція мети
функція мети  ,а в найкращій вершині
,а в найкращій вершині 
 . Розрахунки завершеного “центру ваги”
. Розрахунки завершеного “центру ваги”  протилежної до
протилежної до 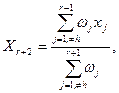 (2.2)
(2.2) - ваги
- ваги  вершин симплекса,
вершин симплекса,  - число незалежних змінних задачі (2.1).
- число незалежних змінних задачі (2.1). (2.3)
(2.3) - координати точки відбиття, а
- координати точки відбиття, а  - коефіцієнт відбиття
- коефіцієнт відбиття  . Отримана точка
. Отримана точка  (2.4)
(2.4) - значення критерію ковзного допуску, обумовлене як
- значення критерію ковзного допуску, обумовлене як

 - номер ітерації,
- номер ітерації, 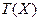 - функціонал над множиною обмежень вид, що має:
- функціонал над множиною обмежень вид, що має: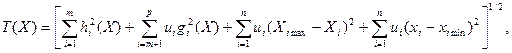
 -функція Хевисайда:
-функція Хевисайда: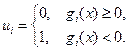
 . Мінімізація T(X) може проводиться тим же алгоритмом послідовного симплексного пошуку.
. Мінімізація T(X) може проводиться тим же алгоритмом послідовного симплексного пошуку. в припустиму область
в припустиму область 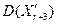 визначається значення функції в ній
визначається значення функції в ній 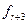 і рівняється зі значеннями функції у вершинах симплекса. Якщо
і рівняється зі значеннями функції у вершинах симплекса. Якщо  , то виконується операція розтягання
, то виконується операція розтягання
 -коефіцієнт розтягання
-коефіцієнт розтягання 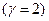 .
.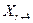 перевіряється нерівність (2.4) і у випадку його виконання точка розтягання вводиться в припустиму область -
перевіряється нерівність (2.4) і у випадку його виконання точка розтягання вводиться в припустиму область - 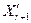 . Якщо
. Якщо  , то з метою підвищення швидкості пошуку проводиться квадратична екстраполяція
, то з метою підвищення швидкості пошуку проводиться квадратична екстраполяція 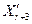 й
й  і
і 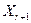 від “центру ваги” симплекса
від “центру ваги” симплекса  , то провести екстраполяцію, як пропонується в /42/, не представляється можливим. Нижче пропонується процедура екстраполяції функції мети, що враховує можливість порушення обмежень задачі в процесі пошуку
, то провести екстраполяцію, як пропонується в /42/, не представляється можливим. Нижче пропонується процедура екстраполяції функції мети, що враховує можливість порушення обмежень задачі в процесі пошуку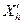 - проекції “гіршої” точки
- проекції “гіршої” точки  . Перед екстраполяцією необхідно визначити проекцію
. Перед екстраполяцією необхідно визначити проекцію 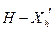 й значення функції в ній
й значення функції в ній 
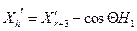 ,
,
 (2.6)
(2.6)
 ,
, 
 , що перебуває на прямій H із крапкою відліку в
, що перебуває на прямій H із крапкою відліку в  (2.7)
(2.7) .
. (2.8)
(2.8) визначається значення функції мети
визначається значення функції мети  , яке потім рівняється с.
, яке потім рівняється с.  Якщо
Якщо 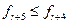 , то
, то  . А якщо ні, то
. А якщо ні, то  , де
, де  ,
, 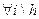 , то відбиття також зізнається вдалим і припустима відбита точка
, то відбиття також зізнається вдалим і припустима відбита точка  , то проводиться наближення відбитої точки
, то проводиться наближення відбитої точки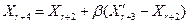 , (2.9)
, (2.9)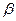 - коефіцієнт стиску
- коефіцієнт стиску  ; якщо
; якщо  , те виконується операція стиску
, те виконується операція стиску (2.10)
(2.10)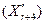 і в ній визначається значення функції мети
і в ній визначається значення функції мети  то виконується операція редукції симплекса до кращої точки
то виконується операція редукції симплекса до кращої точки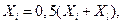
 (2.11)
(2.11)


