Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
II. Метод попарного сравненияСодержание книги
Поиск на нашем сайте
1. При использовании метода попарного сравнения эксперты проводят попарную оценку рассматриваемых факторов в форме матриц. В 1-й строке и 1-м столбце матрицы указываются обозначения оцениваемых факторов, а на пересечении i-й строки и j-го столбца эксперт проставляет оценку i-го фактора по сравнению с j-м фактором. При этом, если фактор Таблицы 3-8 Матрицы попарного сравнения факторов экспертами
2. Определим математическое ожидание попарной оценки сравниваемых факторов. Для этого будем использовать следующие формулы:
где
Получим:
3. Построим матрицу математических ожиданий, куда внесём полученные значения (таблица 9). Таблица 9 Матрица математических ожиданий оценок попарного сравнения факторов
Произведём суммирование по строкам (факторам) таблицы 9. На основании полученных сумм осуществим ранжирование факторов по степени важности. Чем больше сумма баллов
Вывод. Рассмотренные модификации метода экспертных оценок (метод простого ранжирования и метод попарного сравнения) дают тождественный результат. Наиболее значимым для повышения успеваемости группы фактором является время проведения занятий. Далее в порядке убывания значимости следуют: материальная заинтересованность студента; посещаемость; качество преподавания; семейное положение студента; желание учиться и здоровье; уровень организации учебного процесса. Таким образом, чтобы повысить успеваемость группы, необходимо особое внимание обратить на время проведения занятий, размер материальных выплат студентам и посещаемость. Однако следует заметить, что значение коэффициента конкордации меньше 0,5, поэтому желательно повторить рассмотренный процесс или улучшить состав экспертов в целях получения более достоверных оценок рассматриваемых факторов.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 684; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.68.39 (0.006 с.) |

 более значим, чем фактор
более значим, чем фактор  , то это обозначается 1. Если фактор
, то это обозначается 1. Если фактор 


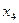




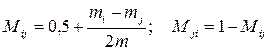 ,
,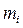 – число предпочтений, отданных экспертом i-му фактору при попарной оценке (количество единиц);
– число предпочтений, отданных экспертом i-му фактору при попарной оценке (количество единиц);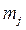 – число предпочтений, отданных экспертом j-му фактору при попарной оценке (количество нулей);
– число предпочтений, отданных экспертом j-му фактору при попарной оценке (количество нулей); – число опрошенных экспертов.
– число опрошенных экспертов.


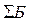 , тем важнее фактор. Таким образом, получим:
, тем важнее фактор. Таким образом, получим: