
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лінійні однорідні диференціальні рівняння другого порядку зі сталими коефіцієнтамиСодержание книги
Поиск на нашем сайте
Розглянемо лінійне однорідне диференціальне рівняння другого порядку
де Теорема 8.3. Частинний розв'язок диференціального рівняння (8.24) має вигляд
Доведення. Покажемо, що функція
Отриманий вираз може мати нульове значення тільки при Всі коефіцієнти характеристичного рівняння є відповідними коефіцієнтами диференціального рівняння. Теорема 8.4. Якщо корені характеристичного рівняння: 1) дійсні і різні
2) дійсні і рівні
3) комплексно спряжені (
1. Нехай корені характеристичного рівняння дійсні і різні:
Отже, згідно з теоремою (8.2) можна сконструювати загальний розв'язок диференціального рівняння (8.24)
2. Нехай корені характеристичного рівняння дійсні і рівні ( За теоремою (8.3) один частинний розв'язок рівняння має вигляд Знайдемо першу і другу похідні цієї функції
Підставимо
3. Нехай корені характеристичного рівняння комплексно спряжені:
Застосовуючи формулу Ейлера, вираз
або
Отримані функції є частинними розв'язками рівняння (8.24), але містять у собі уявну одиницю
або
Приклад 8.10. Знайти частинний розв'язок рівняння Розв’язання. Тут характеристичне рівняння має вигляд Після диференціювання загального розв'язку, одержимо
Підставляючи в початкові умови
Звідки знайдемо, що Отже, частинний розв'язок, що задовольняє зазначеним початковим умовам, має вигляд Приклад 8.11. Знайти загальний розв'язок рівняння Розв’язання. Тут характеристичне рівняння Приклад 8.12. Знайти загальний розв'язок рівняння Розв’язання. Характеристичне рівняння даного диференціального рівняння має вигляд
|
||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 418; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

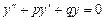 , (8.24)
, (8.24) і
і  – деякі числа.
– деякі числа.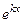 , де число
, де число  – корінь рівняння
– корінь рівняння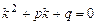 .
.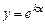 за зазначених умов задовольняє рівняння (8.24). Для даної функції
за зазначених умов задовольняє рівняння (8.24). Для даної функції 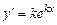 ,
, 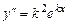 . Підставивши у рівняння (8.24), одержимо
. Підставивши у рівняння (8.24), одержимо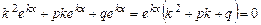 .
.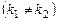 , то загальний розв'язок рівняння (8.24) має вигляд
, то загальний розв'язок рівняння (8.24) має вигляд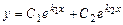 ; (8.25)
; (8.25)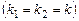 , то загальний розв'язок рівняння (8.24) має вигляд
, то загальний розв'язок рівняння (8.24) має вигляд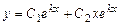 ; (8.26)
; (8.26) ,
, 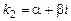 ,
,  ), то загальний розв'язок рівняння (8.24) має вигляд
), то загальний розв'язок рівняння (8.24) має вигляд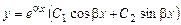 . (8.27)
. (8.27) . Тоді за теоремою (8.3) частинними розв'язками диференціального рівняння (8.24) є функції
. Тоді за теоремою (8.3) частинними розв'язками диференціального рівняння (8.24) є функції 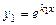 ,
, 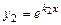 . Ці розв'язки лінійно незалежні, оскільки
. Ці розв'язки лінійно незалежні, оскільки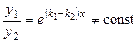 .
.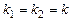 ), що можливо, якщо дискримінант квадратного рівняння
), що можливо, якщо дискримінант квадратного рівняння 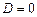 . При цьому, розв’язуючи характеристичне рівняння, одержуємо
. При цьому, розв’язуючи характеристичне рівняння, одержуємо 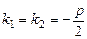 .
.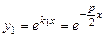 . Інший частинний розв'язок повинен бути лінійно незалежним від першого. Покажемо, що таким розв'язком може бути функція
. Інший частинний розв'язок повинен бути лінійно незалежним від першого. Покажемо, що таким розв'язком може бути функція  . Покажемо, що вона задовольняє рівняння (8.24).
. Покажемо, що вона задовольняє рівняння (8.24).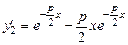 ,
, 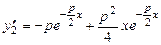 .
. ,
, 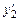 ,
, 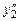 , у диференціальне рівняння (8.24) і після перетворень одержимо
, у диференціальне рівняння (8.24) і після перетворень одержимо  , оскільки за умовою дискримінант характеристичного рівняння
, оскільки за умовою дискримінант характеристичного рівняння 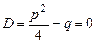 . Отже, функція
. Отже, функція 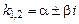 де
де 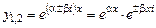 .
.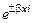 запишемо у вигляді
запишемо у вигляді 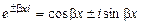 . При цьому частинні розв'язки рівняння (8.24) приймають вигляд
. При цьому частинні розв'язки рівняння (8.24) приймають вигляд
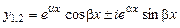 .
.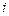 . Неважко показати, що якщо функція
. Неважко показати, що якщо функція 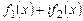 є розв'язком рівняння (8.24), то окремо функції
є розв'язком рівняння (8.24), то окремо функції 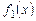 і
і 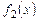 також є його розв'язками. Тому приймемо за перший частинний розв'язок функцію
також є його розв'язками. Тому приймемо за перший частинний розв'язок функцію 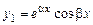 , за другий частинний розв'язок
, за другий частинний розв'язок  . Очевидно, що ці функції лінійно незалежні, тому в такому випадку загальний розв'язок рівняння (8.24) має вигляд
. Очевидно, що ці функції лінійно незалежні, тому в такому випадку загальний розв'язок рівняння (8.24) має вигляд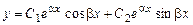
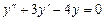 , якщо відомо, що
, якщо відомо, що 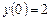 ,
,  .
.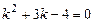 і його корені
і його корені 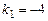 ,
, 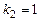 дійсні і різні, тому, застосовуючи формулу (8.25) загальний розв'язок рівняння запишемо у вигляді
дійсні і різні, тому, застосовуючи формулу (8.25) загальний розв'язок рівняння запишемо у вигляді 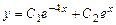 .
.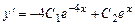 .
. ,
, 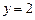 ,
, 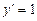 , одержимо систему рівнянь
, одержимо систему рівнянь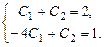
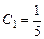 ,
, 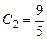 .
. .
. .
.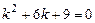 має корені
має корені 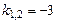 , отже, за формулою (8.26) загальний розв'язок рівняння має вигляд
, отже, за формулою (8.26) загальний розв'язок рівняння має вигляд 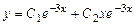 .
.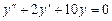 .
.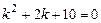 . Його дискримінант
. Його дискримінант 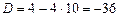 , а
, а 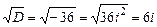 . Корені рівняння
. Корені рівняння 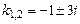 є комплексно спряженими. Тут
є комплексно спряженими. Тут 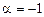 ,
, 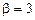 . За формулою (8.27) загальний розв'язок рівняння буде
. За формулою (8.27) загальний розв'язок рівняння буде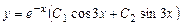 .
.


