
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деякі диференціальні рівняння другого порядку, що допускають зниження порядку.
1. Найпростіше диференціальне рівняння другого порядку має вигляд
Послідовно двічі інтегруючи і тим самим знижуючи порядок рівняння, будемо мати
Приклад 8.7. Знайти частинний розв'язок диференціального рівняння Розв’язання. Загальний розв'язок диференціального рівняння одержуємо, двічі інтегруючи його послідовно:
Підставляючи у вирази початкові умови, одержуємо систему рівнянь для визначення значень
Шуканий частинний розв'язок має вигляд 2. Диференціальне рівняння другого порядку, що не містить явно функції
Введемо нову невідому функцію, прийнявши
Це диференціальне рівняння першого порядку відносно функції
Підставляючи замість
Проінтегрувавши його, одержимо загальний розв'язок даного рівняння
Приклад 8.8. Знайти частинний розв'язок диференціального рівняння Розв’язання. Дане рівняння не містить явно шуканої функції, тому замінимо Знайдемо допоміжну функцію
Складемо систему рівнянь для визначення функцій
Розв’язуючи перше рівняння, знаходимо, що Отже, Інтегруючи, маємо Щоб із загального розв'язку рівняння виділити частинний, який задовольняє початковим умовам Отже, частинний розв'язок даного рівняння має вигляд
3. Диференціальне рівняння другого порядку, що не містить явно незалежної змінної
Таке рівняння допускає зниження порядку, якщо за нову незалежну змінну взяти Тоді, застосувавши правило диференціювання складної функції, одержимо Підставляючи значення
Розв'язок цього рівняння знайдемо у вигляді Замінюючи Приклад 8.9. Знайти загальний розв'язок диференціального рівняння Розв’язання. Дане рівняння не містить у собі явно незалежну змінну Оскільки
|
|||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 299; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.252.201 (0.008 с.) |
 . (8.18)
. (8.18) ,
, ,
, , що задовольняє початковим умовам
, що задовольняє початковим умовам  ,
,  .
. ,
, .
. і
і  :
: звідки
звідки 
 .
. , має вигляд
, має вигляд . (8.19)
. (8.19) ,
,  . Тоді рівняння (8.19) буде
. Тоді рівняння (8.19) буде .
. . Розв’язуючи його, одержуємо
. Розв’язуючи його, одержуємо .
. , приходимо до найпростішого диференціального рівняння першого порядку
, приходимо до найпростішого диференціального рівняння першого порядку .
. .
. , що задовольняє початковим умовам
, що задовольняє початковим умовам  ,
,  .
. , що є лінійним рівнянням першого порядку.
, що є лінійним рівнянням першого порядку. . Тоді
. Тоді  . Підставимо значення
. Підставимо значення  в рівняння і підберемо функції
в рівняння і підберемо функції  і
і  так, щоб виконувалася рівність
так, щоб виконувалася рівність або
або  .
.
 . Підставивши знайдене значення
. Підставивши знайдене значення  .
. або
або  . Але оскільки
. Але оскільки  , то загальний розв'язок заданого рівняння знайдемо, проінтегрувавши функцію
, то загальний розв'язок заданого рівняння знайдемо, проінтегрувавши функцію  .
. .
. ,
,  ,
,  , одержимо, що
, одержимо, що  ,
,  .
. .
. має вигляд
має вигляд . (8.20)
. (8.20) .
. або
або  .
.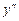 у рівняння (8.20) одержуємо диференціальне рівняння першого порядку відносно функції
у рівняння (8.20) одержуємо диференціальне рівняння першого порядку відносно функції 
 .
. .
. , одержуємо
, одержуємо  – рівняння з подільними змінними. Після поділу змінних прийдемо до рівності
– рівняння з подільними змінними. Після поділу змінних прийдемо до рівності  , інтегруючи яку, знайдемо загальний розв'язок даного рівняння у вигляді
, інтегруючи яку, знайдемо загальний розв'язок даного рівняння у вигляді  .
. .
. ,
,  , яке є рівнянням з подільними змінними. Після поділу змінних прийдемо до рівняння
, яке є рівнянням з подільними змінними. Після поділу змінних прийдемо до рівняння  , інтегруючи яке маємо
, інтегруючи яке маємо  або
або  . Звідки
. Звідки  .
. або
або  . Інтегруючи, одержуємо
. Інтегруючи, одержуємо  – загальний інтеграл заданого рівняння
– загальний інтеграл заданого рівняння


