
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лінійні неоднорідні диференціальні рівняння другого порядку. Метод варіації довільних сталих⇐ ПредыдущаяСтр 12 из 12
Лінійне неоднорідне диференціальне рівняння другого порядку має вигляд
Знання якого-небудь частинного розв'язку рівняння (8.28) дозволяє звести задачу про розв'язання цього рівняння до задачі про розв'язання відповідного однорідного рівняння (8.21). Теорема 8.5. Загальний розв'язок рівняння (8.28) є сумою якого-небудь частинного розв'язку і загального розв'язку відповідного йому однорідного рівняння: Дійсно, якщо
Якщо відомо загальний розв'язок однорідного рівняння (8.21), то загальний розв'язок рівняння (8.28) можна обчислити за допомогою так званого методу варіації довільних сталих, запропонованого Лагранжем. Як знаємо, загальний розв'язок рівняння (8.21) має вигляд Припустимо, що загальний розв'язок рівняння (8.28) має такий же вигляд, але
Підберемо функції Диференціюючи рівність (8.29), одержуємо
Будемо вимагати, щоб
Тоді перша похідна приймає вигляд
Підставляючи в рівняння (8.28) знайдені за умов (8.30) значення
Оскільки функції
Отже, для знаходження функцій Оскільки функції
Зазначимо, що така система має єдиний розв'язок, тому що її визначник є визначником Вронського, який для лінійно незалежних функцій Розв’язуючи систему, знайдемо
де Загальний розв'язок рівняння (8.28) приймає вигляд
причому функція Зазначимо, що метод варіації довільних сталих завжди приводить до розв'язку, але часто буває громіздким через складні інтеграли, за допомогою яких обчислюються функції Приклад 6.13. Знайти загальний розв'язок диференціального рівняння
Розв’язання. Однорідне диференціальне рівняння, що відповідає заданому неоднорідному має вигляд Знайдемо загальний розв'язок заданого рівняння у вигляді
Система (8.32) для даного рівняння приймає вигляд
Розв’язуючи систему, одержимо
Загальний розв'язок рівняння
або після перетворень Тут
|
|||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.110.58 (0.006 с.) |
 . (8.28)
. (8.28)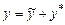 .
.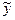 – загальний розв'язок однорідного рівняння, відповідного даному, то
– загальний розв'язок однорідного рівняння, відповідного даному, то 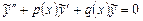 . Якщо
. Якщо 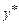 – частинний розв'язок неоднорідного рівняння (8.28), то
– частинний розв'язок неоднорідного рівняння (8.28), то 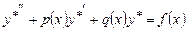 . Покажемо що
. Покажемо що 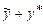 задовольняє рівняння (8.28). Для цього обчислимо першу і другу похідні від
задовольняє рівняння (8.28). Для цього обчислимо першу і другу похідні від 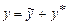 і підставляючи в рівняння (8.28), одержуємо
і підставляючи в рівняння (8.28), одержуємо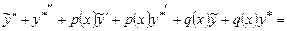
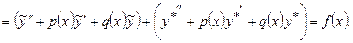
 .
. і
і  – деякі невідомі функції, тобто
– деякі невідомі функції, тобто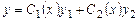 . (8.29)
. (8.29)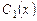 і
і 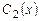 так, щоб вираз (8.29) задовольняв рівняння (8.28).
так, щоб вираз (8.29) задовольняв рівняння (8.28).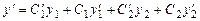 .
.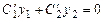 . (8.30)
. (8.30)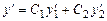 і
і 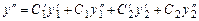 .
. і
і 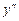 , після перетворень одержуємо
, після перетворень одержуємо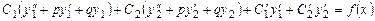 .
. і
і  задовольняють рівняння (8.21), то в останньому рівнянні перші дві дужки дорівнюють нулю і рівняння матиме вигляд
задовольняють рівняння (8.21), то в останньому рівнянні перші дві дужки дорівнюють нулю і рівняння матиме вигляд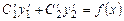 . (8.31)
. (8.31) відомі, то маємо систему двох лінійних рівнянь першого степеня з двома невідомими
відомі, то маємо систему двох лінійних рівнянь першого степеня з двома невідомими 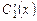 і
і 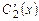 :
: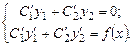 (8.32)
(8.32) .
.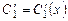 ,
, 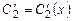 , звідки
, звідки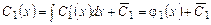 ,
,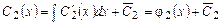 ,
,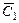 ,
, 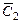 – довільні сталі.
– довільні сталі.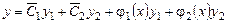 , (8.33)
, (8.33)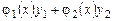 є його частинним розв'язком.
є його частинним розв'язком.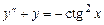 .
. . Його характеристичне рівняння має корені
. Його характеристичне рівняння має корені 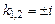 , яким відповідають частинні розв'язки
, яким відповідають частинні розв'язки 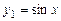 ,
,  .
.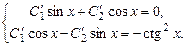

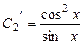 . Знайдемо
. Знайдемо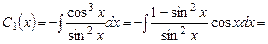
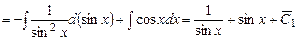 ,
,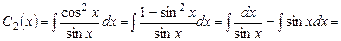
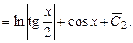
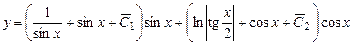
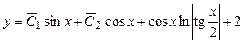 .
.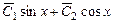 – загальний розв'язок однорідного диференціального рівняння, що відповідає заданому,
– загальний розв'язок однорідного диференціального рівняння, що відповідає заданому, 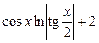 – його частинний розв'язок.
– його частинний розв'язок.


