
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лінійні однорідні диференціальні рівняння другого порядку. Загальні властивості.Содержание книги
Поиск на нашем сайте
Лінійним однорідним диференціальним рівнянням другого порядку називається рівняння виду
де Теорема 8.1. Якщо функції Доведення. Нехай функції
Отже, функція Щоб відповісти на це питання, розглянемо поняття лінійної залежності функцій. Будемо називати функції Очевидно, що якщо функції Так, функції Для лінійно незалежних функцій
Даний визначник, називається визначником Вронського для функцій Отже, для лінійно незалежних функцій Аналогічно, якщо функції Теорема 8.2. Якщо
де Доведення. З теореми 8.1 випливає, що функція Доведемо тепер, що які б не були початкові умови
Визначником даної системи лінійних рівнянь, у якій
а значить система (8.23) має єдиний розв'язок. Отже, для будь-яких початкових умов завжди можна з розв'язку (8.22) знайти частинний розв'язок, що задовольняє їм, а значить розв'язок (8.22) є загальним. З доведеної теореми випливає, що для відшукання загального розв'язку (8.22) досить знайти два лінійно незалежних частинних розв'язки і скласти їхню лінійну комбінацію з довільними сталими.
|
||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 294; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.247.59 (0.008 с.) |

 , (8.21)
, (8.21) і
і  неперервні функції на деякому проміжку;
неперервні функції на деякому проміжку;  – шукана функція.
– шукана функція. і
і  частинні розв'язки рівняння (8.21), то функція
частинні розв'язки рівняння (8.21), то функція  при будь-яких значеннях довільних сталих також є його розв'язком.
при будь-яких значеннях довільних сталих також є його розв'язком. та
та 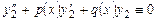 . Покажемо, що функція
. Покажемо, що функція  ,
, 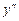 у диференціальне рівняння (8.21), одержимо
у диференціальне рівняння (8.21), одержимо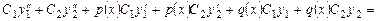

 тільки при
тільки при 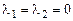 і лінійно залежними, якщо знайдеться хоча б одне відмінне від нуля число
і лінійно залежними, якщо знайдеться хоча б одне відмінне від нуля число  (
( чи
чи  ) таке, що для будь-якого значення аргументу лінійна комбінація
) таке, що для будь-якого значення аргументу лінійна комбінація 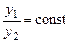 і, якщо функції
і, якщо функції  .
.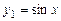 ,
,  лінійно незалежні, тому що
лінійно незалежні, тому що 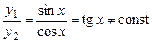 , а функції
, а функції  лінійно залежні, оскільки
лінійно залежні, оскільки 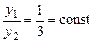 .
. , тобто
, тобто  . А це можливо лише при
. А це можливо лише при 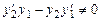 , що за допомогою визначника другого порядку можна записати у вигляді
, що за допомогою визначника другого порядку можна записати у вигляді .
. .
.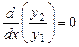 , тобто
, тобто  . Звідки
. Звідки  , а це означає, що визначник Вронського
, а це означає, що визначник Вронського  для будь-якого
для будь-якого  .
. і
і  – довільні сталі, є його загальним розв'язком.
– довільні сталі, є його загальним розв'язком.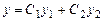 є розв'язком рівняння (8.21) при будь-яких сталих
є розв'язком рівняння (8.21) при будь-яких сталих 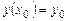 ,
,  , можна так підібрати значення довільних сталих
, можна так підібрати значення довільних сталих  (8.23)
(8.23)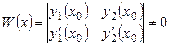 ,
,


