
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основное кинетическое уравнение фильтрования.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ректификация. Принцип действия ректификационной колонны. Материальный баланс ректификации. Равновесие в системе жидкость-пар. Законы Рауля,Дальтона. Понятие азеотропы. Диаграмма t-x,y;y-x. Материальный баланс. Материальный баланс для всей ректификационной установки может быть представлен двумя уравнениями: по всем веществам f p w G = G + G (7.5) по легколетучему компоненту f f p p w w G x = G x + G x, (7.6) где Gf – мольный расход исходной смеси, подаваемой на разделение в колонну, (кмоль)/ч; Gw – мольный расход кубового остатка, отбираемого из колонны, (кмоль)/ч; f p w x, x, x – содержание легколетучего компонента в исходной смеси, дистилляте и кубовом остатке соответственно в мольных долях (мольных процентах). По уравнениям (7.5) и (7.6) определяют расход дистиллята и кубового остатка при известном расходе исходной смеси и содержании легколетучего компонента в исходной смеси, дистилляте и остатке:
Уравнения (7.5)–(7.8) не изменятся, если вместо молярных расходов использовать массовые расходы, а вместо молярных составов – массовые составы. Материальный баланс может быть составлен также для укрепляющей и исчерпывающей частей колонны. При составлении этих материальных балансов в силу допущения 1 удобнее пользоваться мольными расходами и мольными составами. Пересчет массового состава в мольный проводят по формуле
(7.9) где х, Q – мольный и массовый состав смеси соответственно; MA, MB – молекулярная масса легколетучего и высококипящего компонентов соответственно.
Гидравлика 4.Уравнение неразрывности в дифференциальной форме(вывод)
Основы защиты интеллектуальной собственности ТБО (экология) Химический катализ. О скорости процесса Скорость (удельная скорость) химической реакции w rJ - количество (моль) n J одного из реагентов или продуктов, прореагировавших (или образовавшихся) в единицу времени t в единице реакционного пространства
Явления переноса
1. ρ и μ= const (T=const) 2. течение стационарное => 3. течение одномерное wz≠0;wx=wy=0
4. течение жидкости происходит на участке с установившимся течением Запишем ур-ние Навье-Стокса и урав-ние неразрывности 1.
2. Уравнение новье-стокса
 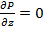
Модифицированное давление p- p gz=P
Пусть (2)=С1, т.е. мы разбиваем выражение (2) на два уравн-ия и => p=C1* z+C2. Зададим граничные условия Z=0; p=pвх; z=L; p=pвых=> ∆p- перепад давлений на участке длины L
Сложим, левые и правые части и подставим в (3)
Уравн-ия (3) в декартовых координатах заменим ур-ниями (8),(9),кот. Являются обыкновенным диф уравнением с частной производной 2-го порядка, для решения кот-го урав. (8)-(9) должны добавится след. Условия однозначности: граничные условия: r=R, wz(R)=0 (10) условие ограниченности wz при 0≤r≤R, wz≠∞ (11) после двухкратного интегрирования (8) получаем
(11)=> A=0; (10) и A=0 => B=∆pR2/4μl Подставляя А и В в (12), получаем решение задачи Пуазейля
Характеризует распределение скорости жидкости в плоскости по координатам x и y,кот.явля-ся параболическим
Характеризует распределение скорости жидкости в плоскости покоординатам x и y,которые являются параболическими.
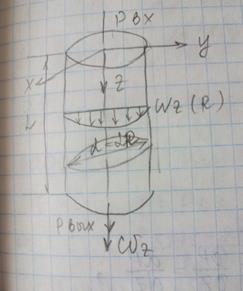
Химическая технология(ОХТ) Химкад. Основное кинетическое уравнение фильтрования. Фильтрование под действием перепада давления. Два режима фильтрования и основные виды фильтрующей аппаратуры. Фильтрование под действием перепада давления. В емкость 1 размещена опорная решетка 4, на которой смонтирована фильтрующая перегородка, состоящая из дренажной сетки 3 и фильтрующей ткани 2. Необходимый перепад давления обеспечивается либо нагнетанием жидкости или газа в обьем аппарата над фильтром, либо созданием вакуума под фильтром. В результате фильтрования на фильтрующей перегородке отлогается осадок.
Основное кинетическое уравнение фильтрования:
Воспользовавшись уравн-ми применительнок движению жидкости через фильтрующую перегородку и через осадок и имея ввиду постоянство расхода жидкости:
Где ∆p1 – перепад давления,вызываемый фильтрующей перегородкой;dτ-время;l-высота слоя зернистого материала; r-удельное сопротивление зернистого материала. Суммируя левые и правые части равенств и преобразуя полученное выражение найдем: dV/Fdτ=(∆p1+∆p2)/(Rф+lr)=∆p/(Rф+lr) где ∆p=∆p1+∆p2- общий перепад давления на фильтре. Высота слоя осадка l=Vx/F,то dV/Fdτ=∆p/(Rф+Vxr/F) или (Vxr/F)dV+RфdV=∆pFdτ –основное кинетическое уравнение фильтрования. Режимы: постоянной разности давлений и постоянной скорости. 1)режим постоянной разности давлений V2xr+2RфVF=2∆pF2τ,решим относительно τ, τ=rl2/(2∆px)+Rфl/(∆px),где ∆p=const и VF=V/F=l/x,VF-удельная производительность фильтра VF= Для режима фильтрования при постоянном перепаде давления продолжительность фильтрования пропорциональна квадрату объема получаемого фильтра. dV/Fdτ=V/Fτ=W=const,решим относительно ∆p и умножим на τ, получим ∆p=W2xrτ+WRф. Для режима с постоянной скоростью перепад давления возрастает по мере увеличения продолжительности фильтрования. Процессы фильтрования усложняются по причинам: взвешенные частицы осаждаются под действием силы тяжести,поэтому толщина слоя осадка растет непропорционально раствору фильтрата; мелкозернистые осадки уплотняются под давлением фильтрования, и их гидравлическое сопротивление r увеличивается с ростом перепада давления rx=ro∆pxn или rx=ro(1+a∆pxm),где rx-удельное сопротивление осадка при любом перепаде давления, ro-удельное сопротивление осадка при перепаде давления в отношении рабочего перепада давления к перепаду давления в опыте;a,m,n- коэффициенты,определяемые опытным путем. В подавляющем случае полученные на фильтрах осадки подвергают промывки для удаления жидкости, входившей в состав суспензии. Продолжительность промывки находится из уравнения dVпр/Fdτ=const то τпр=VпрRобKв/(∆pF), где Kоб-сумма сопротивлений фильтрующей перегородки;Kв-поправочный коэффициент 4 способа задания перепада давления: 1. Гидростатическое фильтрование 2. Вакуумирование пространства под фильтрующей перегородкой(фильтры,в кот. Осуществляется такой способ называются нутч-фильтры) 3. Создание давления над фильтрующей перегородкой(под перегородкой- Pатм, над перегородкой P избыточное) 4. Центробежное фильтрование
|
||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.28.73 (0.012 с.) |

 (7.7)
(7.7) (7.8)
(7.8)



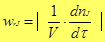 Скорость химических превращений
Скорость химических превращений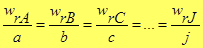 Из законов стехиометрии следует, что
Из законов стехиометрии следует, что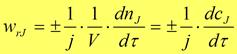
 4.Течение в круглой трубе.
4.Течение в круглой трубе.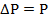 вх-Pвых,,жидкость ньютовская,несжимаемая;течение изотермическое=>допущения:
вх-Pвых,,жидкость ньютовская,несжимаемая;течение изотермическое=>допущения: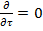
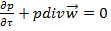
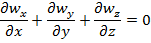
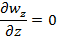
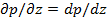
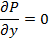
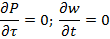
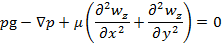
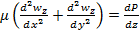 (2)
(2)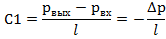
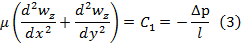
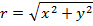
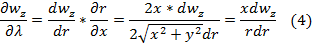
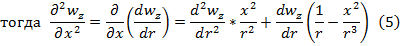
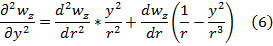
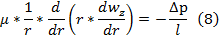 ,где
,где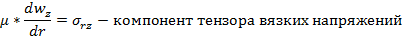
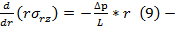 уравнение Коши для течения в цилиндрических трубах с постоянной площадью сечения.
уравнение Коши для течения в цилиндрических трубах с постоянной площадью сечения.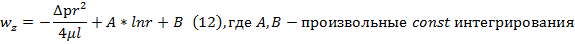
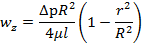
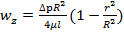 -уравнение Пуазейля
-уравнение Пуазейля
 Будем считать, что в процессе фильтрования не происходит забивки пор фильтрующей перегородки и сопротивление ее в процессе не меняется. Осадок можно рассматривать как слой зернистого материала, а фильтрование жидкости- как движение потока через этот слой и фильтрующую перегородку.
Будем считать, что в процессе фильтрования не происходит забивки пор фильтрующей перегородки и сопротивление ее в процессе не меняется. Осадок можно рассматривать как слой зернистого материала, а фильтрование жидкости- как движение потока через этот слой и фильтрующую перегородку. где dV-обьем жидкости,прошедший через фильтр; dτ – время; F- площадь фильтра; ∆p- перепад давления на фильтре; l – высота слоя зернистого материала; r – удельное сопротивление зернистого материала.
где dV-обьем жидкости,прошедший через фильтр; dτ – время; F- площадь фильтра; ∆p- перепад давления на фильтре; l – высота слоя зернистого материала; r – удельное сопротивление зернистого материала.





