
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамическая характеристика.Содержание книги
Поиск на нашем сайте
Динамическая характеристика объекта показывает, как регулируемая величина в результате регулирующего воздействия изменяется во времени. Изменение регулируемой величины зависит от свойств объекта и от характера возмущения. Наихудшие условия для регулирования имеют место при скачкообразном возмущении. Поэтому параметры объекта принято определять по динамической характеристике, представляющей собой изменение регулируемой величины во времени при скачкообразном изменении положения регулирующего органа. Такая характеристика называется переходной характеристикой объекта или характеристикой разгона.
ПИД – регулятор. ПИД – регуляторам называется регулятор, у которого перемещение РО пропорционально отклонению регулируемой величины от задания, интегралу от этого отклонения и скорости его изменения, т.е.
где Передаточная функция ПИД – регулятора
Как видно из уравнения (13.7), регулирующее воздействие состоит из пропорциональной, интегральной и дифференциальной составляющих. Последняя из них тем больше, чем больше скорость изменения отклонения регулируемой величины, т.е. регулирующее воздействие вырабатывается как бы заранее, не дожидаясь наступления значительного отклонение регулируемой величины. Введение дифференциальной составляющей закон регулирования позволяет улучшить качество переходного процесса в АСР. Однако, настройка ПИД – регулятора, связанная с определением трёх параметров, сложна, при неправильной настройке качество регулирования может оказаться хуже, чем при использовании более простых регуляторов. 3. 3 .Алгебраический критерий устойчивости Гурвица. Алгебраический критерий устойчивости Гурвица применяется для замкнутых систем. Однако, как правило, известна W(s) разомкнутой САУ. В этом случая надо ”мысленно” замкнуть систему единичной обратной отрицательной связью (ООС), найти передаточную функцию замкнутой системы по формуле Wз(s)= и записать характеристическое уравнение системы Q2(s)=0, т.е. a0sn+ a1sn-1+...+ an-1s+ an=0. Формулировка критерия устойчивости Гурвица: для устойчивости замкнутой САУ необходимо и достаточно, чтобы при a0>0 все миноры, расположенные по главной диагонали определителя Гурвица, были строго положительны.
Различают три типа границы устойчивости системы из условия Dn=anDn-1=0 Это следующие границы: 1)первый тип границы устойчивости, который называется апериодической границей устойчивости an=0; 2) второй тип границы устойчивости, который называется колебательной границей устойчивости Dn-1=0; 3) третий тип границы устойчивости называется бесконечной a0=0, когда один из корней характеристического уравнения равен бесконечности, т.е. sj=¥ Следует отметить, что наиболее опасной является нахождение системы на колебательной границы устойчивости.
Билет №24 Функциональная схема АСР.
Каждому элементу принципиальной схемы соответствует блок, имеющий вход и выход. Вход и выход пред-ставлены обобщёнными физическими величинами. РО – регулирующий орган – входит в состав ОУ (реостат с ОВГ); ИМ – исполнительный механизм (двигатель М) - приводит к изменению положения регулирующего органа ОУ; РЕГ – регулятор (УМ); ЗУ – задающее устройство (потенциометр Rз). ЧЭ – чувствительный элемент, датчик (в данной системе специализированное устройство отсутствует). 2 И – регуляторы. И – регулятором называется такой регулятор, у которого скорость перемещения РО пропорционально отклонению регулируемого параметра от заданного значения. Передаточная функция И – регулятора
где У И – регулятора нет жесткой зависимости между отклонением регулируемой величины и положением РО. В момент прекращения работы АР регулирующий орган может занимать любое положение в пределах возможного диапазона перемещений. Основное достоинства И – регуляторов отсутствие остаточного отклонения регулируемой величины по окончании процесса регулирования. Это объясняется тем, что регулирующее воздействие регулятора на объект прекращается в тот момент, когда отклонение регулируемой величины от заданного значения становится равным нулю. Недостатком И – регулятора является относительно низкая скорость, которая характеризуется значением параметра настройки регулятора
3.Принцип регулирования по отклонению. (Принцип обратной связи). АСР по отклонению работает по замкнутому циклу, т.е. имеет обратную связь.
Управляющее воздействие U(t) формируется как функция от отклонения регулируемой величины y(t) от ее предписанного значения x(t): U(t)=F [ E(t) ], где E(t)=x(t) - y(t) y(t) – текущее значение регулируемой величины. x(t) - предписанное значение регулируемой величины (заданное воздействие) Достоинство: Информация о регулируемом параметре поступает на вход АР через ОС и учитывается при формировании управленческого воздействия. Недостаток: 1. Имеет ошибку регулирования при переходном процессе. 2. Имеет свойство к неустойчивости и склонности к колебаниям при работе системы с большим коэффициентом передачи.
Билет №25
|
||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.253.224 (0.01 с.) |

 (13.7)
(13.7) = 1/Тии
= 1/Тии  = Тд – параметры настройки ПИД–регулятора, Тд-время дифференцирования
= Тд – параметры настройки ПИД–регулятора, Тд-время дифференцирования (13.8)
(13.8)

 или
или  (12.3)
(12.3) (12.4)
(12.4)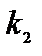 = 1/Ти параметры настройки И – регулятора, Ти - постоянная интегрирования
= 1/Ти параметры настройки И – регулятора, Ти - постоянная интегрирования . Чем больше
. Чем больше 



