
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 7 Программирование рекурсивных алгоритмовСодержание книги
Поиск на нашем сайте
Понятие рекурсии Рекурсия - это способ определения процесса/объекта «в терминах самого себя», в терминах некоторого более простого случая этого же процесса/объекта. Рекурсивные определения используются во многих областях науки, особенно в математике. В математике рекурсией называется способ описания функций или процессов через самих себя. Примером рекурсивно описываемой функции является факториалъная функция: 0! = 1; для всех n > 0 n! = n*(n-1)!, которая для
Здесь уже не очевидно, какая глубина рекурсии будет достигнута при конкретных вычислениях. Однако в общем случае можно утверждать, что указанные рекурсивные вычисления требуют конечной глубины рекурсии. Если описание предназначено для практических вычислений, то глубина рекурсии должна быть конечной. Рекурсивные определения часто используются и в информатике. Например, описание синтаксиса формальных языков с помощью БНФ- нотаций (форм Бэкуса-Наура). В языках программирования рекурсия используется как способ описания подпрограмм (прежде всего функций), содержащих прямо или косвенно обращение к себе самой. Для исполнения таких подпрограмм требуется особая организация вычислительного процесса, так как при рекурсивных вычислениях необходимо сохранение информации об иерархии связей и локальных переменных всех рекурсивных вызовов, чтобы по окончании цепочки рекурсивных вызовов можно было восстановить каждое предшествующее прерванное состояние подпрограммы. Почти все системы рекурсивного программирования основываются на идее стека. Стеком является структура памяти магазинного типа LIFO (Last In First Out) - «последним пришел - первым ушел». Рекурсия вошла в программирование в значительной степени благодаря системам обработки списков и языкам функционального программирования, где использование рекурсии естественно в силу рекурсивной природы реализуемого вычислительного процесса и рекурсивной структуры обрабатываемых данных. Проникновение рекурсивных методов в практику традиционного (императивного) программирования началось с языка Алгол, допускающего рекурсивные обращения к процедурам. Дальнейшая практика рекурсивных вычислений показала, что разумное применение рекурсии является эффективным методом программирования, существенно упрощает запись многих сложных алгоритмов, а в ряде случаев оказывается незаменимым средством. Область практического применения рекурсии - это сложные задачи численного анализа, алгоритмы трансляции, операции над списками, алгоритмы последовательных испытаний и многое другое.
|
||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 215; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.6.9 (0.007 с.) |

 n > 0 определяется рекуррентным соотношением через значение факториала от (n-1); в свою очередь, (n-1)! определяется через (n-2)! и т. д. до сведения к значению 0!, которое определено явно и равно единице. Любое рекурсивное описание должно содержать явное определение функции для некоторых/начальных значений аргумента/аргументов, к которому сводится процесс вычисления значения функции в общем случае. Число промежуточных вычислений этой же функции в процессе вычисления ее значения для заданных аргумента/аргументов - это глубина рекурсии. Для факториальной функции глубина рекурсии при любом значении аргумента очевидна, например при вычислении 3! рекурсия имеет глубину в 3 уровня. Однако обычно глубина рекурсии не является столь очевидной даже при простейших описаниях. Примером может служить рекурсивное определение биномиальных коэффициентов или числа сочетаний
n > 0 определяется рекуррентным соотношением через значение факториала от (n-1); в свою очередь, (n-1)! определяется через (n-2)! и т. д. до сведения к значению 0!, которое определено явно и равно единице. Любое рекурсивное описание должно содержать явное определение функции для некоторых/начальных значений аргумента/аргументов, к которому сводится процесс вычисления значения функции в общем случае. Число промежуточных вычислений этой же функции в процессе вычисления ее значения для заданных аргумента/аргументов - это глубина рекурсии. Для факториальной функции глубина рекурсии при любом значении аргумента очевидна, например при вычислении 3! рекурсия имеет глубину в 3 уровня. Однако обычно глубина рекурсии не является столь очевидной даже при простейших описаниях. Примером может служить рекурсивное определение биномиальных коэффициентов или числа сочетаний  :
: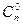 = 1 для п > 0;
= 1 для п > 0;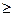 0;
0; +
+  для n
для n 


