
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод прохождения отрезка с переменным шагомСодержание книги
Поиск на нашем сайте
В отличие от двух предыдущих этот метод позволяет найти не один, а несколько корней, если таковые имеются на выбранном интервале. Он предоставляет возможность локализовать каждый из искомых корней (определить все отрезки [ a,b ]). Сами корни находят одним из первых двух методов. Пример 4.15 Суть метода заключается в следующем. 1.Выбирается интервал [ А, В ] значений аргумента Х, на котором ищутся корни. 2.Определяется начальное значение шага Н = (В - А)/ n, где n — начальное количество точек на интервале. 3.Проходят интервал [ А, В ] с шагом Н, вычисляя значения функции f(x) и f(x+H). 4.Если вычисленная пара значений функции имеет разные знаки, корень локализован. Его можно определить, например методом Ньютона. После нахождения корня отступают от него на величину шага Н. 5.Уменьшают шаг, например: Н: = Н / 2 6.Пункты 3 — 5 выполняют до тех пор, пока не будут найдены все корни. Program Roots; Const n= 20; { начальное количество точек на интервале } Var A, B, X, y1, y2, lev, Prav, E: Real; Predpol, Naideno: Integer; { количества корней } Function f(x: Real): Real; Begin f:= { здесь должна быть формула для вычисления функции} End; Function Prf(x: Real): Real; Begin Prf:= { здесь будет формула для вычисления производной} End; Procedure Newton(Lev,E: Real; Var x:Real); { нахождение корня методом Ньютона } { Lev - левая граница, x - корень } Var Y, xn: Real; Begin x:= Lev; { вычисление корня } Repeat xn:= x-f(x)/Prf(x); y:= Abs(xn-x); x:= xn; Until y <= E; X:= xn; End; Begin Writeln('Введите интервал нахождения корней и погрешность'); Readln(A, B, E); Writeln('Введите предполагаемое количество корней'); Readln(Predpol); { Начальный шаг } H:=(B-A)/2; { Поиск корней } Repeat Naideno:=0; { найдено корней } X:=A; While x < B do Begin Y1:= f(x); Y2:= f(x+H); If ((y1>=0) And (y2<0))Or((y1<0) And (y2>=0)) then Begin { корень локализован } Lev:= x; Newton(Lev, E, x); Y1:= f(x); Writeln('Корень = ', Xsl:8:4); Writeln('Функция = ', y2:10:7); End; X:= x + H; End; H:= H / 2; Until (Predpol = Naideno) Or (H <= E); If Predpol <> Naideno Then Writeln('Количество корней задано неверно'); Writeln('Работа окончена'); Readln; End. Вычисление определенных интегралов Известно, что определенный интеграл некоторой функции на f(x) интервале [ a,b ] равен площади фигуры, ограниченной кривой f(x), осью х и вертикальными линиями, проходящими через границы интервала. Вычисление такого интеграла приближенными методами предполагает замену указанной фигуры более простыми, площади которых можно найти по формулам, применяемым в элементарной геометрии. Очевидно, что чем меньше размеры элементарных фигур — тем точнее результат. Если разность между двумя последовательными приближениями окажется меньше заданной погрешности Е, то последнее значение можно считать результатом.
Общий алгоритм вычисления определенного интеграла можно представить следующим образом. 1. Ввести a, b и Е. 2. Вычислить начальное значение площади (приближение). 3. Повторять Вычислить очередное приближение Пока абсолютная величина разности между соседними приближениями не будет меньше или равна Е. 4. Закончить. В качестве элементарных фигур, которыми заменяется исходная, наиболее часто используют прямоугольники или трапеции. Соответственно методы приближенного вычисления определенного интеграла называют: 1. Метод прямоугольников и 2. Метод трапеций. Метод прямоугольников Метод основан на замене площади сложной фигуры суммой площадей прямоугольников, высота которых равна значению функции f(x), а ширина — hx, шагу по оси х. Очевидно, что чем меньше шаг, тем точнее аппроксимация. Площадь элементарного прямоугольника равна f(x)* hx. Алгоритм вычисления определенного интеграла рассматриваемым методом может быт таким. 1. Ввести a, b и Е. 2.1. Начальное значение шага hx = (b-a)/n, где n — начальное количество точек; 2.2. Вычислить площадь S 1 = S S прямоуг (hx) 2.3. Повторять 2.3.1. hx:= hx / 2; 2.3.2. Вычислить площадь S 2 = S S прямоуг (hx); 2.3.3. Y:= | S2 - S1 |; 2.3.4. S1:= S2 Пока не будет y £ Е. 2.4. Вывести S 2. 3. Закончить. В приведенном алгоритме дважды вычисляется сумма площадей элементарных прямоугольников. Эту операцию можно оформить в виде процедуры или функции. Пример 4.16 Программа, которая реализует описанный алгоритм с использованием функции f(x) и процедуры вычисления площади методом прямоугольников приведена ниже. Program Integral; Const n= 20; { начальное количество точек на интервале } Var a, b, hx, s1, s2, E, y: Real; Function f(x: Real): Real; Begin f:= { здесь должна быть формула для вычисления функции} End; Procedure S_Rect(a,b,h:Real; Var S:Real); { вычисление интеграла методом прямоугольников } { a и b — границы интервала, h — шаг по оси х }
{ S — результат } Var X: Real; Begin S:=0; X:=a; While x<b do Begin S:= S + f(x)*h; x:= x+h; End; End; Begin { основная программа } Writeln('Введите интервал и погрешность'); Readln(a, b, E); { Начальный шаг } hx:=(b-a)/n; { Начальное значение интеграла (площади) } S_Rect(a,b,hx,s1); { Вычисление очередных приближений } Repeat hx:=(b-a)/2; S_Rect(a,b,hx,s2); y:=Abs(s2-s1); s1:=s2; Until y <= E; Writeln('Интеграл = ', s2:10:6); Writeln('Работа окончена'); Readln; End. Метод трапеций Метод основан на замене площади сложной фигуры суммой площадей трапеций, высота которых равна шагу по оси х (hx), а основания — значениям функции f(x) и f(x + hx). Очевидно, что он позволяет точнее аппроксимировать функцию и быстрее получить результат. В этом можно убедиться, подсчитав количество приближений обоими методами. Из геометрии известно, что площадь элементарной трапеции равна (f(x) + f(x + hx)) / (2* hx). Алгоритм вычисления определенного интеграла рассматриваемым методом отличается от предыдущего только процедурой нахождения площадей s1 и s2. Эта процедура может быть предствалена в следующем виде. Procedure S_Trap(a,b,h:Real; Var S:Real); { вычисление интеграла методом трапеций } { a и b — границы интервала, h — шаг по оси х } { S — результат } Var X: Real; Begin S:=0; X:=a; While x<b do Begin S:= S + (f(x) + f(x + h)) / (2* h).; x:= x+h; End; End; Вызов в основной программе с именем Integral процедуры S_Trap вместо S_Rect позволит реализовать в ней метод трапеций. Пример 4.17 Найти сумму ряда x y = x - ----- + ----- - ----- + … 2! 3! 4! С точностью Составим программу: x Program iter; a = a *----- общий член ряда. uses crt; i var y = y +a cумма ряда. x, y, a: real; i = integer; esp: = real; begin Clr Scr; - очищение экрана Writeln (' введите x, esp'); readln (' x, esp);
While abc (a)>esp do begin Вычисление суммы ряда - Writeln ('y=', y, ' кол. итер.=', i); end. 1шаг 2 шаг 3 шаг a = (-1)*(x/1) a = -(x)*(x/2) a = -(-x a = +x a = x
|
||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 204; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.253.53 (0.007 с.) |

 x
x 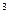 x
x 
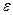 = 10
= 10 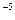 , точность считается достигнутой, если очередной член ряда по модулю <
, точность считается достигнутой, если очередной член ряда по модулю <  определение начальных значений.
определение начальных значений.



