Использование статистических

Методов

Из данного приложении вы узнаете, как:

• определять степень взаимосвязанности двух переменных, вычисляя наиболее часто используемый коэффициент корреляции — пирсоново г;

• проводить простой регрессионный анализ

• двумя способами находить хи-квадрат (%²), т. е. проводить проверку номинальных данных;

• осуществлять проверку по критерию Стьюдента;

Разумное применение статистических методов

Один из важнейших навыков психолога-исследователя состоит в способности выбрать подходящий вид статистического анализа. В главах 4,7-9 вы уже частично познакомились с этим процессом. Из главы 4 вы узнали о различных видах шкалы измерений (номинальной, порядковой, интервальной и шкалы отношений) и о различиях между описательной статистикой и статистикой вывода. Также вы узнали, как вычислять некоторые общие величины, используемые в описательной статистике, например среднее арифметическое и стандартное отклонение, и познакомились с процедурой проверки гипотез. Главы 4,7 и 8 познакомили вас с проверкой по критерию Стьюдента и дисперсионным анализом (ANOVA), применяемым при заключительном анализе эксперимента. В главе 9 были описаны коэффициенты корреляции.

Из этого приложения вы узнаете, как выбрать подходящий вид анализа для полученных вами данных в соответствии с выбранным планом исследования, как проводить такой анализ и интерпретировать результаты с помощью статистических таблиц. Возможно, вы будете пользоваться пакетами программ, например Statistical Package for Social Sciences (SPSS), которые предназначены для машинной статистической обработки результатов, но изучение примеров, приведенных в этом приложении, позволит вам лучше понять, как осуществляются подобные процедуры.

Какой вариант статистического анализа использовать — зависит от различных факторов, в том числе от: а) цели анализа: изучить взаимосвязь или провести срав-

нение, б) использованной шкалы измерений, в) особенностей плана исследования: например, является ли независимая переменная меж- или внутрисубъектной, и в некоторых случаях от г) размера выборки.

Если цель анализа — определить степень взаимосвязи двух изучаемых переменных, потребуется вычислить коэффициент корреляции. Самый общий из них — пирсоново г. Он используется, если измерения проводятся по интервальной шкале или шкале отношений. При использовании порядковой шкалы вычисляется «эр» Спирмена (обозначается г), показывающее степень взаимосвязи между двумя наборами порядковых данных. В случае номинальных данных также можно измерить взаимосвязь (коэффициент сопряженности — С). Ниже приведен пример вычисления пирсонова г. Как найти г и С, можно узнать из учебника по статистике.

Если целью анализа является сравнение двух или более экспериментальных условий, чтобы обнаружить существующие между ними различия, можно воспользоваться несколькими методами анализа. Приведенные в данном приложении примеры иллюстрируют некоторые наиболее общие подходы: проверку по критерию хи-квадрат (х²), {/-тест Мэнна—Уитни, проверку по критерию Стьюдента и дисперсионный анализ (ANOVA). Проверка по критерию х-квадрат проводится, если получены номинальные данные, в случае порядковых данных используется U-тест Мэнна—Уитни. Проверка по критерию Стьюдента и ANOVA требуют, чтобы данные были получены по интервальной шкале или шкале отношений.

Оценка взаимосвязей

Пример 1. Пирсоново г

Если обе переменные измеряются либо по интервальной шкале, либо по шкале отношений, их взаимосвязь можно оценить с помощью пирсонова г. Предположим, к примеру, что исследователь хочет определить взаимосвязь между количеством времени, бесполезно потраченного студентами, и их средним баллом. Средний балл варьируется от 0,0 до 4,0, а потраченное без пользы время — это количество часов, проводимых в неделю за определенными занятиями (например, просмотром мыльных опер). Для девяти студентов получены следующие данные.

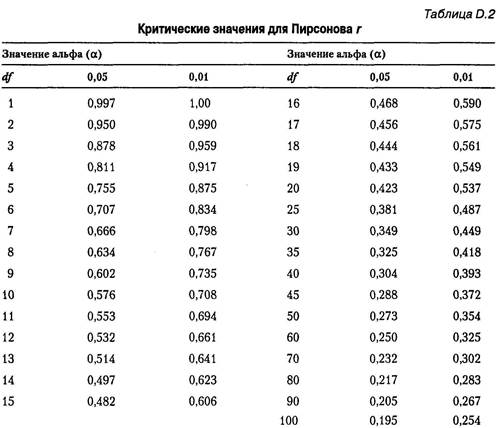
Шаг 3. Определите, является ли г значимым (т. е. отличается ли от нуля). Узнать это можно с помощью табл. D.2 приложения D, в которой приведены «критические значения» (cv - critical values) величины г. Сначала определите степень свободы (df - degree of freedom). Для Пирсонова rdf= N- 2, где N— это количество пар оценок. В нашем примере df = 8 -2 = 6. В строке таблицы, где df=&, вы найдете два критических значения: одно для уровня значимости, равного 0,05 (cv — 0,707), и второе для 0,01 (cv = 0,834). Если найденное значение равняется или превышает критическое значение, то можно отвергнуть нулевую гипотезу о том, что г-0. Это означает возможность вывода о том, что корреляция является статистически значимой. В данном случае значение -0,89 является значимым при уровне значимости 0,01, так как оно больше критического значения, равного 0,834. Таким образом, вероятность того, что найденное значение корреляции (-0,89) является случайностью, очень мала (0,01 или 1 из 100). Является ли значение корреляции положительным или отрицательным, не важно — учитывается его абсолютное значение. Если вы внимательно изучите таблицу D.2, то сможете заметить один важный факт, касающийся корреляции. Если у вас всего несколько пар оценок (как в приведенном выше примере), корреляция должна быть довольно высокой, чтобы ее можно было охарактеризовать как значимую. Имея лишь несколько пар оценок, довольно легко случайно получить высокое значение корреляции. С другой стороны, при большом количестве пар оценок корреляция, кажущаяся весьма низкой, может тем не менее быть значимой.

Пример 2. Регрессионный анализ

Из главы 9 вы узнали о том, что наличие корреляции дает возможность делать прогнозы с помощью процедуры, называемой «регрессионным анализом». В ходе анализа определяется линия регрессии, которая служит основой для построения прогнозов. Ниже показан регрессионный анализ примера исследования взаимосвязи бесполезно потраченного времени и среднего балла. Формула для нахождения линии регрессии:

Y-a + bX,

где а = точка на оси У; Ь = наклон кривой; Х= известное значение; У = предполагаемое значение.

Шаг 1. Вычислите все составляющие:

s_x где г = пирсоново г = -0,89;

s = стандартное отклонение (см. табл. 4.4); 5_у = 0,63; s_x = 9,43;

Ь = -0,89^ = (0,89)(0,07) = -0,06. 9,43

а =?-ЬХ,

где у = среднее арифметическое для Y = 2,80;

X = среднее арифметическое для X — 28,88;

а = 2,80 - (-0,06)(28,88) = 4,53.

Шаг 2. Подставьте значения для точки на оси Yu наклона кривой в формулу регрессии:

Y - а + ЬХ - 4,53 + (-О.Об)Х - 4,53 - 0.06Х.

Шаг 3. Используйте формулу для предположений.

Если Патрик потратил без пользы 40 часов, каков его предположительный средний балл?

7=4,53-0,06.

X = 4,53 - (0,06)(40) = 4,53 - 2,40 = 2,13.

Если Патриция потратила 20 часов без пользы, каков ее предположительный средний балл?

У- 4,53 -0,06.

X - 4,53 - (0,06)(20) = 4,53 - 1,20 = 3,33.

Оценка различий

Пример 3. Степень согласия %²

Если отчет о данных включает в себя указание числа попаданий некоторого явления в определенную категорию, то становится ясно, что использована номинальная шкала измерений. Чтобы определить, является ли частота этого события систематической величиной или просто случайностью, требуется провести заключительную проверку номинальных данных. Проверка по критерию хи-квадрат (%²) — это наиболее общая статистическая процедура, используемая в случае номинальных данных. Есть две разновидности этой процедуры, различающиеся в зависимости от того, сколько наборов значений получено, один или два. Процедуру, используемую в случае одного набора значений, иногда называют «степень согласия %²», так как с ее помощью определяют, отклоняется ли частота, полученная в исследовании, от частоты, ожидаемой по теории вероятности или в соответствии с конкретной предсказываемой моделью.

В качестве примера предположим, что у студентов складывается мнение, будто используемые преподавателем задания на выбор ответа содержат искажения: пять вариантов ответа не одинаково часто являются правильными. Им кажется, что варианты б, в и г являются правильными чаще, чем а или д. Преподаватель заинтересовался этим вопросом и решил оценить все задания на выбор ответа, использованные в предыдущем семестре. Было подсчитано, сколько раз выбирается каждый из вариантов ответа. Если искажение отсутствует, это значение должно быть примерно одинаковым для всех вариантов. Таким образом, нулевая гипотеза говорит, что для каждого из вариантов ожидаемая частота выбора будет одинаковой. Общее количество вариантов в заданиях на выбор ответа равняется 400, а следовательно, ожидаемая частота (Е) для каждого из вариантов равняется 400/5 = 80. В действительности получены следующие значения частоты:

Вариант а: 62.

Вариант б: 85.

Вариант в: 78.

Вариант г: 111.

Вариант д: 64.

Итого: 400.

488 Приложение С, Использование статистических методов

Шаг 1 Вычислите все составляющиеО-Е: 62- 80 = -18;

85-80= +5;78-80= -2;111-80 = +31;64-80= -16. (О-Е)²: (-18)²=324;

(+5)²= 25; (-2)²= 4; (+31)²=961; (-16)²= 256.

Шаг 2 Подставьте составляющие в формулу для х² и найдите его значение:

Шаг 3 Определите, значимо ли найденное значение у}.

В табл. D.3 приведены «критические значения» для %². Степень свободы для х² в случае одной выборки равняется количеству категорий минус 1, в данном случае 4 (5 - 1 = 4). В строке таблицы для df= 4 находятся два критических значения: одно для уровня значимости 0,05 (cv — 9,49), а второе —для уровня 0,01 (о)= 13,28). Найденное значение превышает оба критических значения, а следовательно, коэффициент %² значим при уровне значимости 0,01. Преподаватель сделает вывод, что в распределении вариантов правильных ответов для задания на выбор присутствует некоторое искажение. Варианты а и д действительно используются реже других.

Пример 4. х² - два набора значений

В исследованиях по психологии чаще всего находят х², если получено более одного набора значений частоты. Наиболее распространенный вариант — использование двух различных групп испытуемых и разделение членов каждой группы на одну или несколько категорий в зависимости от изучаемого вопроса. Предположим, к примеру, что исследователь хочет определить, влияют ли половые различия на выбор определенных предметов в качестве профилирующих. Чтобы выяснить количество мужчин и женщин, выбравших психологию, биологию и математику, изучаются заявления, подаваемые поступающими студентами (т. е. проводится архивная процедура). В следующей таблице, называемой «факторной таблицей», приведены полученные результаты:

Нулевая гипотеза говорит, что на выбор предметов не влияют половые различия. Для проверки нулевой гипотезы для полученных значений частоты находится х². Формула для х² в случае двух наборов значений:

Шаг 4 Определите, значимо ли найденное значение %².

Степень свободы для %² в случае двух наборов значений равняется: (кол-во рядов - 1)(кол-во столбцов - 1) = (3 -1)(2 - 1) = 2.

В табл. D.3 в строке для df= 2 критические значения равны 5,99 (уровень значимости 0,05) и 9,21 (уровень 0,01). Найденное значение, равное 6,66, больше первого критического значения, но меньше второго, а следовательно, коэффициент х² значим для уровня значимости 0,05, но не для 0,01. Половые различия влияют на выбор профилирующего предмета: значительно больше женщин показали интерес к психологии и значительно больше мужчин — к математике. И женщины, и мужчины показали одинаковый интерес к биологии.

Пример 5. Проверка по критерию Стьюдента — независимые группы

В исследованиях с одной независимой переменной, принимающей всего два значения, различия между двумя наборами оценок часто оцениваются с помощью критерия Стьюдента. Как вы помните из главы 7, есть два основных вида проверки по критерию Стьюдента — они различаются в зависимости от того, являются ли группы испытуемых, на которых получены оценки, независимыми или нет. Независимые группы образуются, если испытуемые распределяются случайным образом или используется субъектная переменная, например пол или возраст. Такие экспериментальные планы требуют проверки по критерию Стьюдента для независимых групп. Проверка по критерию Стьюдента для зависимых групп (иногда называемых «коррелированными» группами) используется, когда одни и те же испытуемые изучаются при обоих условиях эксперимента или если разные группы участников определенным образом взаимосвязаны — либо посредством процедуры уравнивания (см. пример 7), либо с помощью естественного уравнивания, которое наблюдается в случае сравнения родителей с детьми. Ниже представлен простой способ вычисления коэффициента Стьюдента для независимых групп. Для вычислений используется дисперсия, которая, как вы помните из главы 4, является важным показателем изменчивости набора оценок, и находится ее квадратный корень, что дает стандартное отклонение. Более подробно о вычислении стандартного отклонения см. табл. 4.4. В целом, при проверке по критерию Стьюдента для независимых групп сравниваются различия между группами с дисперсией в пределах каждой группы. Исследователи надеются, что различия между группами будут огромными, тогда как изменчивость в пределах групп будет небольшой.

Предположим, исследователь проводит простой эксперимент с памятью и с помощью случайного распределения сформировал две группы испытуемых. Одна группа изучает список из 25 слов при скорости показа 2 с на слово, а другая — при скорости 4 с на слово. Ниже приведено количество слов, запомненных пятью членами каждой группы.

В ходе проверки по критерию Стьюдента разница между двумя средними арифметическими, полученными по результатам эксперимента, делится на «стандартную ошибку различия» — предположительную оценку того, как сильно должны расходиться значения среднего арифметического при влиянии случайных факторов или возникновении ошибки. Исследователь надеется на то, что числитель будет большим, а знаменатель — маленьким, а следовательно, будет большим значение t. В таком случае различия между средними арифметическими будут больше, чем ожидается при воздействии только случайных факторов.

Шаг 2. Подставьте составляющие в формулу и вычислите значение t.

Шаг 3. Определите, является ли найденное значение t значимым.

Степень свободы для коэффициента Стьюдента для независимых групп равняется:

(п, + п₂-2)-(5 + 5-2)-8. В табл. D5 представлен список критических значений для оценки результатов проверки по критерию Стьюдента. В строке, где df= 8, критические значения равняются 2,31 (уровень значимости 0,05) и 3,36 (уровень значимости 0,01). Найденное значение 4,13 превосходит оба из них (знак минус не учитывается), а следовательно, t значимо для уровня 0,01. В данном случае будет разумно отвергнуть нулевую гипотезу и заключить, что у испытуемых, которым демонстрировали слова с разной скоростью, запоминание различается.

Шаг 4. Оцените силу эффекта.

Как вы помните из главы 4, обычно исследователи не только выясняют, являются ли различия между значениями среднего арифметического статистически значимыми, но также определяют относительную силу эффекта, вызываемого экспериментальным воздействием. При проверке по критерию Стьюдента сила эффекта равняется величине изменчивости зависимой переменной, вызываемой независимой переменной (Cohen, 1988). Существуют различные способы оценки силы эффекта; один из наиболее распространенных — коэново d. Чтобы его вычислить, необходимо найти разность между значениями среднего арифметического и разделить ее на предполагаемое стандартное отклонение в популяции, значение которого находится для обоих групп:

Чтобы найти предполагаемое стандартное отклонение в популяции, необходимо сложить значения дисперсии для двух групп и из полученного значения извлечь квадратный корень. Получаем:

s = V5,3 = 6,7=^ = 3,46.

Тогда сила эффекта равняется:

_J=13,4-19,8 3,46

Что означает такой результат? Согласно общим принципам, предложенным Коэном (процитировано в Spatz, 1997), силу эффекта можно разделить на малую (около 0,2), среднюю (около 0,5) и большую (около 0,8). По этому стандарту 1,85 — это очень большой эффект (знак минус можно не учитывать, он лишь показывает, какое из значений среднего арифметического стоит первым в числителе). Таким образом, увеличение ско-

рости показа с 2 до 4 секунд на слово в данном примере имеет заметное влияние на запоминание.

Примечание, анализ силы эффекта можно провести для второго вида проверки по критерию Стьюдента, с которым вы сейчас познакомитесь, а также для различных видов ANOVA (анализа дисперсии). Чтобы изучить конкретные процедуры, обратитесь к учебнику по статистике.

Пример 6. Проверка по критерию Стьюдента — зависимые группы

Как было отмечено ранее, проверка по критерию Стьюдента для зависимых групп проводится, если используются планы с повторяемыми измерениями и уравненными группами, а независимая переменная принимает два значения. Каждая пара оценок будет иметь определенные внутренние взаимосвязи, поскольку получена от: а) испытуемых, имеющих некоторое сходство между собой, или б) одних и тех же испытуемых. Так же как коэффициент Стьюдента для независимых групп, в случае зависимых групп этот коэффициент отражает отношение действительных различий между значениями среднего арифметического к изменчивости в пределах каждого условия. Процедура включает вычисление корреляции между двумя наборами оценок и подстановку этого значения в формулу для нахождения коэффициента Стьюдента. В приведенном ниже примере используется упрощенная формула, позволяющая проводить непосредственное вычисление коэффициента Стьюдента без предварительного нахождения пирсонова г.

Предположим, что исследователь для сравнения двух способов обучения компьютерной грамотности — курса для самостоятельного изучения и обычного лекционного курса — использует план с уравненными группами. 10 студентов в каждой группе были уравнены по среднему баллу и коэффициенту вербального интеллекта. Так, пара испытуемых N1 (см. ниже) состоит из двух человек, имеющих примерно одинаковые средний балл и уровень интеллекта. Зависимая переменная может принимать максимальное значение, равное 35. Ниже приведены данные исследования и результаты предварительного анализа, включающего вычисление DhD² для каждой пары оценок.

Шаг 3. Определите, является ли найденное значение t значимым.

Степень свободы для коэффициента Стьюдента для независимых групп равняется количеству пар оценок минус 1, в данном случае ^=10-1 = 9. Снова воспользуйтесь табл. D.5. Для строки, в которой df = 9, критические значения равны 2,26 (уровень значимости 0,05) и 3,25 (уровень значимости 0,01). Найденное значение (6,63) превышает оба критических значения, а следовательно, г значим при уровне значимости 0,01. Таким образом, курс для самостоятельного изучения эффективнее традиционного лекционного курса.

ПРИЛОЖЕНИЕ О

Статистическиетаблицы

В данном приложении вы найдете таблицы, используемые, когда необходимо принять статистически обоснованное решение:

Таблица D1. Случайные числа.

Таблица D2. Критические значения для пирсонова г.

Таблица D3. Критические значения для хи-квадрат (%²).

Таблица DA. Критические значения для [/-теста Мэнна—Уитни.

Таблица D5. Критические значения для распределения t (двусторонний тест).

Таблица D6. Критические значения для распределения F.

Таблица D. 1 Случайные числа

 

Источник: Fisher, R.A., & Yates, F. (1963) Statistical tables for biological, agricultural, and medical research (6^th ed.). Table VII. Edinburg: Oliver & Boyd.

 

Чтобы U, вычисленное на основании полученных данных, было значимым, его значение должно равняться или быть ниже, чем значение, приведенное в таблице. Прочерки в ячейках таблицы означают, что для установленного уровня значимости решение принять невозможно. Источник: Kirk, R. Е (1984). Elementary Statistics. Belmont, CA: Brooks/Cole.

 

 

 

 

 

 

ПРИЛОЖЕНИЕ Е

Ответы к заданиям для повторения

В этом приложении даны ответы к приведенным в конце каждой главы заданиям на множественный выбор и некоторым упражнениям. В ответах к заданиям на множественный выбор в скобках указывается номер страницы, на которой излагается соответствующий материал. В руководстве для преподавателей приведен полный список ответов к упражнениям.