
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства функции распределения двумерной случайной величиныСодержание книги
Поиск на нашем сайте
1. Функция распределения Утверждение следует из того, что 2. Функция распределения при при 3. Если хотя бы один из аргументов обращается в
Функция распределения 4. Если один из аргументов обращается в
где Произведение события 5. Если оба аргумента равны Это следует из того, что совместное осуществление достоверных событий Наиболее полным, исчерпывающим описанием многомерной случайной величины является закон ее распределения. При конечном множестве возможных значений многомерной случайной величины такой закон может быть задан в форме таблицы (матрицы), содержащей всевозможные сочетания значений каждой из одномерных случайных величин, входящих в систему, и соответствующие им вероятности. Так, если рассматривается двумерная случайная величина
Таблица 4.1
Здесь Функция распределения имеет вид
Чтобы по таблице распределения найти вероятность того, что одномерная случайная величина примет определенное значение, надо просуммировать вероятности Определение. Условным законом распределения одной из одномерных составляющих двумерной случайной величины
Если зафиксировать значение одного из аргументов, например положить
Аналогично, условное распределение случайной величины
Случайные величины
В противном случае, при невыполнении этого равенства, случайные величины Определение. Зависимость между двумя случайными величинами называется вероятностной (стохастической или статистической), если каждому значению одной из них соответствует определенное (условное) распределение другой.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 196; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.92.96 (0.007 с.) |

 есть неотрицательная функция, заключенная между нулем и единицей, т.е.
есть неотрицательная функция, заключенная между нулем и единицей, т.е.  .
. есть вероятность.
есть вероятность.
 ,
,

 .
. , функция распределения
, функция распределения  .
. и их произведения представляют невозможные события.
и их произведения представляют невозможные события. , функция распределения
, функция распределения  ,
, ,
, и
и  – функции распределения случайных величин
– функции распределения случайных величин  и
и  , т.е.
, т.е. 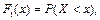
 .
.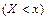 и достоверного события
и достоверного события 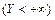 есть само событие
есть само событие  . Аналогично можно показать, что
. Аналогично можно показать, что  .
. .
. есть событие достоверное.
есть событие достоверное. , то ее двумерное распределение можно представить в виде таблицы (матрицы) распределения, в каждой клетке
, то ее двумерное распределение можно представить в виде таблицы (матрицы) распределения, в каждой клетке  которой располагаются вероятности произведения событий:
которой располагаются вероятности произведения событий:  .
.








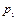













 ;
;  , с условием нормировки:
, с условием нормировки:  .
. , где
, где 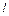 – единичные ступенчатые функции. Единичной ступенчатой функцией называется функция вида
– единичные ступенчатые функции. Единичной ступенчатой функцией называется функция вида
 из соответствующей этому значению строки (столбца) данной таблицы.
из соответствующей этому значению строки (столбца) данной таблицы. , то полученное распределение случайной величины
, то полученное распределение случайной величины  при условии
при условии 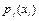 этого распределения будут условными вероятностями события
этого распределения будут условными вероятностями события  , найденными в предположении, что событие
, найденными в предположении, что событие  .
. .
. называются независимыми, если их совместная функция распределения
называются независимыми, если их совместная функция распределения  .
.


