
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Повторные независимые испытанияСодержание книги Поиск на нашем сайте
Схема испытаний Бернулли. Формула Бернулли Предположим, что производится Теорема. Пусть в опыте
Доказательство. Данная формула доказывается следующим образом. Рассмотрим события
где
Следствия: 1) если 2) 2.2. Предельное поведение вероятностей Несмотря на элементарность формулы Формула Пуассона Теорема Пуассона. Если вероятность
Доказательство. Воспользуемся формулой Бернулли:
Учитывая, что Так как
то Строго говоря, условие теоремы Пуассона
При больших Простейший поток событий Во многих практических ситуациях приходится выяснять закономерности появления определенного типа событий: прибытие судов в порт, отказов в работе устройств и т.д. Расчет многих предприятий, например количество парикмахерских, количество касс в магазине, число коек в больнице, число шлюзов на реке и т.д., связано с так называемым потоком событий. Определение. Поток событий называется простейшим, если он обладает следующими свойствами: – стационарности – для любой группы конечного числа непересекающихся интервалов времени появление в них соответственно – отсутствия последействия – вероятность поступления k событий в некоторый промежуток времени не зависит от того, сколько событий и как поступило до этого промежутка времени; – ординарности – невозможность появления двух и более событий за очень маленький промежуток времени. Обозначим через Можно доказать, что вероятность того, что за время
где 2.2.3. Наивероятнейшее число появления события Если Рассмотрим два соседних числа: Между ними имеет место одно из трех соотношений:
Рассмотрим первое соотношение, т.е. Воспользуемся формулой Бернулли
Раскроем скобки и соберем слагаемые с
Итак, если
Т.е при
Если Теорема о вероятности наивероятнейшего числа успехов. Для расчета вероятности наивероятнейшего числа успехов используется формула, дающая приближенный результат. Точность формулы зависит от числа испытаний и по мере увеличения их числа возрастает:
|
||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.242.169 (0.01 с.) |

 независимых испытаний, каждое из которых может иметь два исхода: «успех» с вероятностью
независимых испытаний, каждое из которых может иметь два исхода: «успех» с вероятностью  и «неудачу» с вероятностью
и «неудачу» с вероятностью  . Такая схема называется схемой Бернулли. Термины «успех» и «неудача» употребляются лишь в силу традиции. Важно лишь наличие двух различных исходов испытания.
. Такая схема называется схемой Бернулли. Термины «успех» и «неудача» употребляются лишь в силу традиции. Важно лишь наличие двух различных исходов испытания. производится
производится  независимых испытаний в одних и тех же условиях, причем некоторое событие
независимых испытаний в одних и тех же условиях, причем некоторое событие  в каждом опыте появляется с одной и той же вероятностью
в каждом опыте появляется с одной и той же вероятностью  события
события  , состоящего в том, что в
, состоящего в том, что в  раз, вычисляется по формуле Бернулли:
раз, вычисляется по формуле Бернулли:
 и
и 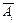 , которые заключаются в том, что событие
, которые заключаются в том, что событие  -м испытании,
-м испытании,  . Тогда очевидно:
. Тогда очевидно: ,
, . Все события
. Все события  ,
,  , несовместны по построению. Следовательно, получаем
, несовместны по построению. Следовательно, получаем

 то используют формулу Бернулли;
то используют формулу Бернулли; .
.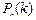

 =
=  , при больших
, при больших  при неограниченном увеличении числа
при неограниченном увеличении числа  , причем произведение
, причем произведение  стремится к постоянному числу
стремится к постоянному числу  , то вероятность того, что событие
, то вероятность того, что событие 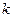 раз в
раз в 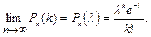
 .
. т.е. при достаточно больших
т.е. при достаточно больших  , тогда
, тогда 
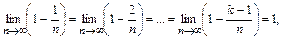
 и
и 

 при
при  , так что
, так что  , противоречит исходной предпосылке схемы испытаний Бернулли, согласно которой вероятность наступления события в каждом испытании
, противоречит исходной предпосылке схемы испытаний Бернулли, согласно которой вероятность наступления события в каждом испытании  . Однако если вероятность
. Однако если вероятность  – незначительно (будем полагать, что
– незначительно (будем полагать, что  ), то приближенная формула Пуассона верна.
), то приближенная формула Пуассона верна. . Если
. Если 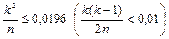 , то относительная погрешность составляет 1%.
, то относительная погрешность составляет 1%. событий зависит только от этих чисел и от длин промежутков времени;
событий зависит только от этих чисел и от длин промежутков времени; промежуток времени, который нас интересует, через
промежуток времени, который нас интересует, через  интенсивность потока, т.е. количество событий за единицу времени.
интенсивность потока, т.е. количество событий за единицу времени. ,
, – среднее число появления события за
– среднее число появления события за 
 . Выясним, при каком значении аргумента эта функция достигает максимума, проще говоря, какое из чисел
. Выясним, при каком значении аргумента эта функция достигает максимума, проще говоря, какое из чисел  является наибольшим.
является наибольшим. .
. ,
, 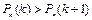 ,
, 
 , т.к.
, т.к.  .
. ;
;  и учитывая, что
и учитывая, что  , получим
, получим или
или  .
. , так как
, так как  , то
, то  . Пусть
. Пусть 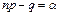 и тогда
и тогда  . Аналогично, рассматривая соотношения
. Аналогично, рассматривая соотношения 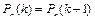 , получим
, получим  и
и  .
. , то
, то 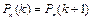 , (если
, (если  – целое);
– целое);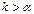 функция
функция  , которое заключено между
, которое заключено между  :
:  или
или  .
. .
.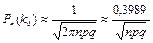 .
.


