
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства дисперсии случайной величиныСодержание книги Поиск на нашем сайте
1. Дисперсия постоянной величины равна нулю
2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат: Учитывая свойство математического ожидания, получим:
3. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом её математического ожидания:
Или
Доказательство. Пусть Тогда
4. Дисперсия алгебраической суммы конечного числа независимых случайных величин равна сумме их дисперсий:
Доказательство.
Обозначая
Обращаем внимание на то, что дисперсия как суммы, так и разности независимых случайных величин
5. Дисперсия центрированной случайной величины равна Доказательство.
6. Дисперсия нормированной случайной величины равна 1. Доказательство.
Определение. Модой Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным. Определение. Медианой
Квантилем уровня
Под Некоторые квантили получили особое название. Очевидно, что введенная выше медиана случайной величины есть квантиль уровня 0,5, т.е. Определение. Начальными Замечание. Для дискретной случайной величины интегралы заменяются суммами:
Замечание. Центральный момент второго порядка
Центральные моменты
и т.д. Например,
(при выводе учли, что Выше отмечено, что математическое ожидание Центральный момент третьего порядка Полученная величина
Если распределение симметрично относительно математического ожидания, то коэффициент асимметрии Центральный момент четвертого порядка Эксцессом случайной величины называется число
Если распределение симметрично относительно математического ожидания, то эксцесс Кривые, более островершинные, чем нормальная, обладают положительным эксцессом, более плосковершинные – отрицательным эксцессом.
|
|||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 147; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.12.234 (0.008 с.) |

 .
. .
. .
.
 .
. , где
, где  .
. .
. . Учитывая, что а – величина постоянная, неслучайная, найдем
. Учитывая, что а – величина постоянная, неслучайная, найдем .
. .
. .
.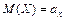 ,
,  и учитывая, что для независимых случайных величин
и учитывая, что для независимых случайных величин 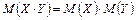 , получим:
, получим: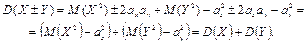
 и
и  равна сумме их дисперсий, т.е.
равна сумме их дисперсий, т.е. .
. .
. .
. .
. случайной величины
случайной величины  или плотность вероятности
или плотность вероятности  достигает максимума).
достигает максимума). непрерывной случайной величины
непрерывной случайной величины  .
. (или q -квантилем) называется такое значение
(или q -квантилем) называется такое значение  случайной величины, при котором функция её распределения принимает значение, равное
случайной величины, при котором функция её распределения принимает значение, равное  .
. -й точкой подразумевается квантиль
-й точкой подразумевается квантиль  , т.е. такое значение случайной величины
, т.е. такое значение случайной величины  .
. . Квантили
. Квантили  и
и  получили название соответственно верхнего и нижнего квартилей.
получили название соответственно верхнего и нижнего квартилей.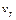 и центральными
и центральными  моментами порядка
моментами порядка  непрерывной случайной величины
непрерывной случайной величины 

 является дисперсией случайной величины
является дисперсией случайной величины  .
.

 – неслучайная величина).
– неслучайная величина). , или начальный момент первого порядка, характеризует среднее значение или положение распределения случайной величины
, или начальный момент первого порядка, характеризует среднее значение или положение распределения случайной величины  , – степень рассеяния распределения
, – степень рассеяния распределения  служит для характеристики асимметрии (скошенности) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, её делят на
служит для характеристики асимметрии (скошенности) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, её делят на  , где
, где  – среднее квадратическое отклонение случайной величины
– среднее квадратическое отклонение случайной величины  называется коэффициентом асимметрии случайной величины:
называется коэффициентом асимметрии случайной величины: .
. .
. служит для характеристики крутости (островершинности или плосковершинности) распределения.
служит для характеристики крутости (островершинности или плосковершинности) распределения.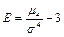 .
. .
.


