
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Одияко, Н.Н., Голодная, Н.Ю.Содержание книги Поиск на нашем сайте
Н.н. одияко Н.Ю. ГОЛОДНАЯ
ТЕОРИЯ ВЕРОЯТНОСТЕЙ Учебное пособие
Рекомендовано Дальневосточным региональным учебно-методическим центром (ДВ РУМЦ) в качестве учебного пособия для студентов направления 080700.62 «Бизнес-информатика» и специальности 080116.65 «Математические методы в экономике» вузов региона
Владивосток Издательство ВГУЭС ББК 22.171 О 42
Рецензенты: А.Ю. Чеботарев, д-р физ.-мат. наук, зав. каф. математической физики и компьютерного моделирования ИМКН ДВГУ; В.Н. Гемба, канд. экон. наук, доцент каф. математики и моделирования ТГЭУ
Одияко, Н.Н., Голодная, Н.Ю. О 42 ТЕОРИЯ ВЕРОЯТНОСТЕЙ [Текст]: учебное пособие. – Владивосток: Изд-во ВГУЭС, 2010. – 232 с.
ISBN
Учебное пособие разработано в соответствии с программой курса, а также требованиями образовательного стандарта России. Излагаются основы теории вероятностей. Основные понятия иллюстрируются различными примерами экономического содержания. Содержит достаточно большое количество решённых задач, задачи для самостоятельного решения и по 30 вариантов индивидуальных заданий по различным разделам дисциплины. Предназначено студентам специальностей 080116.65 «Математические методы в экономике» и 080700.62 «Бизнес-информатика».
ББК 22.171
ISBN © Издательство Владивостокский
экономики и сервиса, 2010 ВВЕДЕНИЕ Настоящее учебное пособие достаточно полно освещает основные положения теории вероятностей в соответствии с программой дисциплины «Теория вероятностей» и Государственного стандарта по специальности «Математические методы в экономике». Оно может быть использовано при изучении раздела «Теория вероятностей» дисциплины «Высшая математика» студентами всех специальностей вуза. Поэтому большинство примеров и задач имеют социально-экономическую направленность. С этой же целью в пособии излагается материал, показывающий связь теории вероятностей и математической статистики с конкретными экономическими приложениями. Изложение ведется от частного к общему, от простого к сложному. Это создает возможности для ведения индивидуального преподавания, позволяет использовать основной материал для разных экономических специальностей, а более сложный – для студентов специальности «Математические методы в экономике». Каждый преподаватель, основываясь на программе конкретной специальности, определяет, какой материал следует давать более подробно, а какой – менее подробно или вообще опустить, рекомендовать к самостоятельному изучению.
Пособие включает в себя основы теории вероятностей: случайные события и их вероятности; случайные величины, их распределения и числовые характеристики; важнейшие предельные теоремы теории вероятностей; введение в теорию случайных процессов. Теория вероятностей изучает свойства массовых случайных событий, способных многократно повторяться при воспроизведении определенного комплекса условий. Основное свойство любого случайного события, независимо от его природы, – мера или вероятность его осуществления. Теория вероятностей – математическая наука. Из первоначально заданной системы аксиом вытекают другие ее положения и теоремы. Впервые законченную систему аксиом сформулировал в 1936 г. советский математик академик А.Н. Колмогоров в своей книге «Основные понятия теории вероятностей». Теория вероятностей вначале развивалась как прикладная дисциплина. В связи с этим ее понятия и выводы имели окраску тех областей знаний, в которых были получены. Лишь постепенно выкристаллизовалось то общее, что присуще вероятностным схемам, независимо от области их приложения: массовые случайные события, действия над ними и их вероятности, случайные величины и их числовые характеристики. Большой вклад в развитие теории вероятностей внесли русские и советские ученые. Приложения способствовали зарождению теории вероятностей, они же питают ее развитие как науки, приводя; к появлению все новых ее ветвей и разделов. На теорию вероятностей опирается математическая статистика, задача которой состоит в том, чтобы по ограниченным данным (выборке) восстановить с определенной степенью достоверности характеристики, присущие генеральной совокупности, т.е. всему мыслимому набору данных, описывающему изучаемое явление. За несколько последних десятилетий от теории вероятностей «отпочковались» такие отрасли науки, как теория случайных процессов, теория массового обслуживания, теория информации, эконометрическое моделирование и др. Этот процесс продолжается и теперь.
Одной из важнейших сфер приложения теории вероятностей является экономика. В настоящее время трудно себе представить исследование и прогнозирование экономических явлений без использования эконометрического моделирования, регрессионного анализа, трендовых и сглаживающей моделей и других методов, опирающихся на теорию вероятностей. С развитием общества народное хозяйство все более усложняется; следовательно, по законам развития динамических систем должен усиливаться статистический характер законов, описывающих социально-экономические явления. Все это предопределяет необходимость овладения методами теории вероятностей как инструментом статистического анализа и прогнозирования экономических явлений и процессов. Тема 1. СЛУЧАЙНЫЕ СОБЫТИЯ Основные понятия комбинаторики Для успешного решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики. Комбинаторикой называют раздел математики, в котором изучаются задачи следующего типа: сколько комбинаций, удовлетворяющих тем или иным условиям, можно составить из элементов данного множества. Алгебра событий Определение. События Определение. Суммой событий Определение. Произведением событий Определение. Разностью событий Определение. Событие
Графически соотношения демонстрируют диаграммы Венна:
Определение. События Замечание. Все законы алгебры высказываний будут верны и для событий, например: Вероятность события Геометрические» вероятности Рассмотрим «геометрические» вероятности: это пример опыта с непрерывным пространством элементарных событий. В случае опыта с равновероятными исходами вероятность
где
Для отрезка – это длина отрезка, для плоскости – площадь фигуры, для тела – объем тела. 1.3.5. Условная вероятность. Определение. Условной вероятностью По определению Рассмотрим формулу для опыта, сводящегося к схеме случаев: Пусть событиям
Теорема. Доказательство. Так как
Учитывая, что Следствие. Определение. События Определение. Формула Теорема. В определении условной вероятности мы требовали, чтобы Пусть Доказательство. Представим событие Так как Теорема. Если события Доказательство. Так как Теорема. Если Доказать самостоятельно. Определение. События Определение. Если любые два события из Теорема. Если события Доказательство. Если события Последнее равенство является необходимым и достаточным условием независимости событий. Замечание. На практике правило умножения вероятностей применяется вместе с правилом сложения вероятностей. Формула полной вероятности Определение. Предположим, что событие Теорема. Пусть с опытом
Доказательство. По условию событие
Данная формула используется в опытах, не сводящихся к схеме случаев.
Формулы Байеса Теорема. Пусть с опытом
Доказательство. Так как Откуда
Замечание. Формулы Байеса предназначены для вычисления после проведения опыта вероятностей гипотез при условии, что событие Решение типовых задач Пример 1. На станцию прибыли 10 вагонов разной продукции. Вагоны помечены номерами от одного до десяти. Найти вероятность того, что, среди пяти выбранных для контрольного вскрытия вагонов окажутся вагоны с номерами 2 и 5? Решение. Событие Воспользуемся формулой Общее число возможных комбинаций для контрольного вскрытия равно числу сочетаний из 10 по 5, т.е.
Пример 2. Из 20 акционерных обществ (АО) четыре являются банкротами. Гражданин приобрел по одной акции шести АО. Какова вероятность того, что среди купленных акций две окажутся акциями банкротов? Решение.Событие Воспользуемся формулой Общее число комбинаций выбора АО равно числу сочетаний из 20 по 6, т.е.
Пример 3. На полке находится 10 книг, расставленных в произвольном порядке. Из них три книги по теории вероятностей, три – по математическому анализу и четыре – по линейной алгебре. Студент случайным образом достает одну книгу. Какова вероятность того, что он возьмет книгу по теории вероятностей или по линейной алгебре? Решение. Событие событие Вероятности того, что студент взял книгу по теории вероятностей и по линейной алгебре соответственно таковы:
События
Пример 4. Контролер проверяет изделия на соответствие стандарту. Известно, что вероятность соответствия стандарту изделий равна 0,9. Какова вероятность того, что из двух проверенных изделий оба будут стандартными, если события появления стандартных изделий независимы? Какова вероятность того, что из двух проверенных изделий только одно стандартное? Решение: а) учитывая то, что события
б) пусть Аналогично
Если обозначить вероятность появления стандартного изделия через
В данном случае
Пример 5. В районе 100 поселков. В пяти из них находятся пункты проката сельхозтехники. Случайным образом отобраны два поселка. Какова вероятность того, что в них окажутся пункты проката? Решение. Пусть Вероятность события
Рассмотрим событие
Искомая вероятность найдется как вероятность произведения зависимых двух событий
Пример 6. На автозавод поступили двигатели от трех моторных заводов. От первого завода поступило 10 двигателей, от второго – 6 и от третьего – 4 двигателя. Вероятности безотказной работы этих двигателей в течение гарантийного срока соответственно равны 0,9; 0,8; 0,7. Какова вероятность того, что: а) установленный на машине двигатель будет работать без дефектов в течение гарантийного срока; б) проработавший без дефекта двигатель изготовлен на первом заводе, на втором заводе? Решение. Обозначим через
а) вероятность того, что наугад взятый двигатель проработает без дефектов, найдем по формуле полной вероятности:
б) если двигатель проработал без дефектов гарантийный срок, то вероятности того, что оно изготовлен на первом, на втором заводах, найдем по формуле Байеса:
1.5. Задачи для самостоятельного решения 1. Некто, набирая номер телефона, забыл две последние цифры номера телефона абонента, но помнит, что последняя цифра меньше предпоследней. Какова вероятность того, что при однократном пользовании телефоном-автоматом, некто наберет нужный номер телефона. 2. Для студенческой лотереи были пронумерованы 500 билетов номерами от 1 до 500. Организаторы лотереи сделали ее беспроигрышной. Все выигрыши разделили на три вида: а) «самый большой выигрыш» – том стихов Пушкина – приходится на билеты, номера которых содержат три одинаковых цифры; б) «средний выигрыш» – набор фломастеров – приходится на билеты, номера которых содержат две одинаковых цифры. Определить вероятность того, что: а) взятый наудачу билет окажется выигрышным; б) на взятый билет выиграют «средний выигрыш»; в) на взятый билет выиграют «большой выигрыш». 3. Имеются 50 экзаменационных билетов, каждый из которых содержит два вопроса. Экзаменующийся знает ответ не на все 100 вопросов, а только на 60. Определить вероятность того, что экзамен будет сдан, если для этого достаточно ответить на оба вопроса из своего билета, или на один вопрос из своего билета, или на один (по выбору преподавателя) вопрос из дополнительного билета. 4. При стрельбе была получена частота попадания 0,6. Сколько было сделано выстрелов, если получено 12 промахов? 5. Из пяти карточек с буквами А, Б, В, Г, Д наугад одна за другой выбираются три и располагаются в ряд в порядке появления. Какова вероятность, что получится слово «ДВА»? 6. В коробке 3 белых и 7 черных шаров. Какова вероятность того, что вынутые наугад два окажутся черными? 7. В лифт семиэтажного дома на первом этаже вошло 4 человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со второго. Найти вероятность того, что 1) все пассажиры выйдут на четвертом этаже; 2) все пассажиры выйдут одновременно; 3) все пассажиры выйдут на разных этажах. 8. Стержень длины 9. После бури на участке между 40-м и 70-м километрами телефонной линии произошел обрыв провода. Какова вероятность того, что разрыв произошел между 50-м и 55-м километрами линии? 10. Считается равновероятным попадание снаряда в любую точку площади в 10000 11. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадает также и в кольцо, образованное построенными окружностями. Предполагается, что попадание точки на плоскость большого круга равновозможно для любой части его. 12. Какой толщины должна быть монета, чтобы вероятность падения на ребро была бы 13. Общество из 14. Два охотника стреляют в волка, причем каждый делает по одному выстрелу. Для первого охотника вероятность попадания в цель 0,7, для второго – 0,8. Какова вероятность попадания в волка (хотя бы при одном выстреле)? Как изменится результат, если охотники сделают по два выстрела? 15. В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся: а) одно окрашенное изделие; б) два окрашенных изделия. 16. Из 100 изготовленных деталей 10 имеют дефект. Для проверки были отобраны пять деталей. Какова вероятность того, что среди отобранных деталей две окажутся бракованными? 17. В группе из 10 студентов, пришедших на экзамен, 3 подготовлены отлично, 4 – хорошо, 2 – посредственно и 1 – плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный – на 16, посредственно – на 10, плохо – на 5. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что студент подготовлен: а) отлично; б) плохо. 18. В продажу поступили 1000 пальто с трех фабрик. С первой фабрики поступили 300 пальто, среди них 10 второсортных, со второй фабрики поступили 450 пальто, среди них 12 второсортных. С третьей фабрики поступили 250 пальто, среди них 8 второсортных. Покупателю подали для примерки пальто первого сорта. На какой фабрике вероятнее всего пошито это пальто? 19. Вероятность появления брака на первом станке равна 0,02, на втором – 0,01 и на третьем – 0,03. Производительность первого станка вдвое больше третьего, а производительность второго станка в 4 раза больше производительности первого станка. Детали, изготовленные на трех станках, хранятся на одном складе. Кладовщик взял наудачу одну деталь, она оказалась стандартной. На каком из станков вероятнее всего была изготовлена эта деталь. 20. Некоторый механизм состоит из 3 деталей типа А, пяти деталей типа Б, двух деталей типа В, шести деталей типа Г и четырех деталей типа Д. Вероятность повреждения детали тапа А равна 0,02, типа Б – 0,05, типа В – 0,10, типа Г – 0,03, типа Д – 0,09. Механизм вышел из строя. Какого типа деталь вероятнее всего повреждена? 21. В первой коробке 35 радиоламп, среди них 4 нестандартных. Во второй коробке 20 радиоламп, среди них 1 нестандартная. В третьей коробке 45 радиоламп, среди них 5 нестандартных. Из третьей коробки взяли наудачу 1 радиолампу и переложили во вторую коробку. Затем из второй коробки была наудачу взята радиолампа и переложена в первую коробку. После этого из первой коробки наудачу извлекли радиолампу. Какова вероятность того, что эта лампа стандартная? 22. В порт приходят корабли только из трех пунктов отправления. Вероятность появления корабля из первого пункта равна 0,2, из второго пункта – 0,6. Найти вероятность прибытия корабля из третьего пункта. 23. Имеются два одинаковых ящика с шарами. В первом ящике 2 белых и 1 черный шар, во втором – 1 белый и 4 черных шара. Наудачу выбирают один ящик и вынимают из него шар. Какова вероятность, что вынутый шар окажется белым? 24. В цехе работают 20 станков. Из них 10 марки 25. Имеются два ящика: в первом 3 белых шара и 2 черных; во втором 4 белых и 4 черных. Из первого ящика во второй перекладывают, не глядя, два шара. После этого из второго ящика берут один шар. Найти вероятность того, что этот шар будет белым. 26. Предположим, что 5% всех мужчин и 0,25% всех женщин дальтоники. Наугад выбранное лицо страдает дальтонизмом. Какова вероятность того, что это мужчина? Считать, что мужчин и женщин одинаковое число. 27. На фабрике, изготовляющей болты, первая машина производит 25%, вторая – 35%, третья – 40% всех изделий. В их продукции брак составляет соответственно 5%, 4% и 2%. Какова вероятность того, что случайно выбранный болт дефектный? Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен первой, второй, третьей машиной? 1.6. Индивидуальные домашние задания Вариант 1 1. Из полного набора костей берут наугад 5 костей домино. Найти вероятность того, что среди них хотя бы одна будет с шестёркой. 2. В партии из 15 деталей имебтся 10 стандартных. Наудачу отобраны 7 деталей. Найти вероятность того, что среди отобранных деталей 5 стандартных. 3. Буквы, составляющие слово «Одесса» написаны по одной на 6 карточках. Карточки смешиваются. Затем по одной вынимаются 3 карточки. Определить вероятность того, что, записывая подряд слева направо, получим слово «сад». 4. У рыбака есть 3 излюбленных места для ловли рыбы, которые он посещает с равной вероятностью каждое. Если он ловит на первом месте, рыба клюёт с вероятностью 0,3; на втором – 0,4; на третьем – 0,3. Известно, что рыбак, выйдя на ловлю, три раза закинул удочку, а рыба клюнула только один раз. Найти вероятность того, что он удил рыбу на первом месте. 5. Электролампы изготовляются на трёх заводах. Первый завод производит 45% общего количества электроламп, второй – 40%, третий – 15%. Продукция первого завода содержит 70% стандартных ламп, второго – 80%, третьего – 81%. В магазин поступает продукция всех трёх заводов. Какова вероятность, что купленная в магазине лампа окажется стандартной. 6. Два стрелка производят по одному выстрелу в мишень. Вероятность попадания первым стрелком равна 0,9; а вторым – 0,8. Найти вероятность того, что мишень поразит только один стрелок. 7. Четыре пловца взяли старт на соревнованиях по плаванию. Вероятность уложиться в рекордное время у первого пловца равна 0,95, у второго – 0,92, у третьего – 0,9 и у четвертого – 0,88. Найти вероятности того, что а) все пловцы станут рекордсменами; б) только два пловца станут рекордсменами. Вариант 2 1. В студенческой группе 10 дружинников. Среди них трое в возрасте 18–19 лет, пятеро – от 20 до 22 лет, двое – от 23 до 24. Путём жеребьёвки из дружинников должен быть выбран один человек на дежурство. Какова вероятность того, что его возраст окажется от 18 до 22 лет. 2. Вероятность попадания в цель первого стрелка равна 0,3, второго – 0,1. Стрелки выстрелили одновременно. Какова вероятность того, что один из них попадает в цель, другой не попадает? 3. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик наудачу взял один валик, а затем второй. Найти вероятность того, что один из взятых валиков конусный, а второй эллиптический с точностью до 0,01. 4. В группе из 10 студентов, пришедших на экзамен, 3 подготовились отлично, 4 – хорошо, 2 – посредственно, 1 – плохо. Всего 20 вопросов. Отлично подготовленный студент может ответить на 20 вопросов, хорошо – на 16, посредственно – на 10, плохо – на 5. Вызванный наудачу студент ответил на 3 произвольно заданных вопроса. Найти вероятность того, что этот студент подготовлен: 1) отлично, 2) плохо. 5. Стрельба производится по 5 мишеням типа А, по 3 типа В, по 2 типа С. Вероятность попадания в мишень типа А равна 0,4; В – 0,1; С – 0,15. Найти вероятность поражения мишени. 6. Из полн
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 139; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.65.133 (0.013 с.) |

 и
и  называются равными:
называются равными:  , если
, если  ,
,  .
.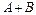 , состоящее в том, что в опыте произойдет хотя бы одно из этих событий.
, состоящее в том, что в опыте произойдет хотя бы одно из этих событий. , состоящее в одновременном появлении этих событий.
, состоящее в одновременном появлении этих событий. и
и  , состоящее в том, что событие
, состоящее в том, что событие  называется противоположным событию
называется противоположным событию  ,
,  до
до  и
и  .
.
 Æ.
Æ. ,
,  ,
,  .
. определяется как «доля» тех исходов, которые приводят к наступлению события
определяется как «доля» тех исходов, которые приводят к наступлению события  ,
, – мера тех исходов, которые приводят к наступлению
– мера тех исходов, которые приводят к наступлению  – мера бесконечного числа исходов.
– мера бесконечного числа исходов. события
события  называется вероятность осуществления события
называется вероятность осуществления события  .
. случаев соответственно из всех
случаев соответственно из всех  возможных и равновозможных случаев. Допустим, что событие
возможных и равновозможных случаев. Допустим, что событие  , причем из них только
, причем из них только  случаев благоприятствуют событию
случаев благоприятствуют событию  .
. .
. , то
, то  .
. (свойство умножения событий), получим
(свойство умножения событий), получим  .
. .
. , то есть,
, то есть,  – условная вероятность события
– условная вероятность события 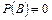 , но в некоторых случаях такое ограничение представляется ненужным.
, но в некоторых случаях такое ограничение представляется ненужным. , тогда равенство
, тогда равенство  выполняется автоматически.
выполняется автоматически. , тогда
, тогда  . Так как
. Так как  , то
, то  . Но так как
. Но так как  и
и  , то
, то  и
и  .
. , то
, то  . Это значит, что если
. Это значит, что если  , тогда
, тогда  и из того, что
и из того, что  , следует, что
, следует, что  ,
, 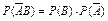 , а это значит, что
, а это значит, что  .
. называются независимыми (в совокупности), если вероятность появления любого из них
называются независимыми (в совокупности), если вероятность появления любого из них  не меняется при наступлении какого угодно числа событий
не меняется при наступлении какого угодно числа событий  из этой же совокупности.
из этой же совокупности. ,
,  и так далее. Тогда
и так далее. Тогда  .
. может наступить только вместе с одним из нескольких попарно несовместных событий
может наступить только вместе с одним из нескольких попарно несовместных событий  , образующих полную группу. Условимся называть эти события (по отношению к
, образующих полную группу. Условимся называть эти события (по отношению к  .
. , так как
, так как  попарно несовместны, то и события
попарно несовместны, то и события  попарно несовместны, следовательно, по аксиоме 3 из определения вероятности события
попарно несовместны, следовательно, по аксиоме 3 из определения вероятности события  и по теореме о вероятности произведения событий получаем
и по теореме о вероятности произведения событий получаем .
. . До опыта были известны вероятности гипотез
. До опыта были известны вероятности гипотез  и соответствующие условные вероятности
и соответствующие условные вероятности  . В этом случае условная вероятность гипотезы при условии, что событие
. В этом случае условная вероятность гипотезы при условии, что событие  .
. и
и  .
. , то
, то  .
.
 .
. . Число исходов, благоприятствующих данному событию, будет равно числу таких комбинаций, в которых две цифры будут 2 и 5, а остальные будут составлять сочетания, число которых равно
. Число исходов, благоприятствующих данному событию, будет равно числу таких комбинаций, в которых две цифры будут 2 и 5, а остальные будут составлять сочетания, число которых равно  . Тогда искомая вероятность будет равна
. Тогда искомая вероятность будет равна
 . Число благоприятствующих исходов определяется как произведение
. Число благоприятствующих исходов определяется как произведение  , где первый сомножитель указывает число комбинаций выбора АО-банкротов из четырех. Но с каждой такой комбинацией могут встретиться АО, не являющиеся банкротами. Число комбинаций таких АО будет
, где первый сомножитель указывает число комбинаций выбора АО-банкротов из четырех. Но с каждой такой комбинацией могут встретиться АО, не являющиеся банкротами. Число комбинаций таких АО будет  . Тогда искомая вероятность будет равна
. Тогда искомая вероятность будет равна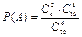 , т.е.
, т.е.  .
. ,
,  .
. и
и  несовместны. Поэтому искомая вероятность находится как сумма вероятностей:
несовместны. Поэтому искомая вероятность находится как сумма вероятностей: .
. (первое изделие стандартное) и
(первое изделие стандартное) и  (второе изделие стандартное) независимы, используем формулу
(второе изделие стандартное) независимы, используем формулу , т.е.
, т.е.  ;
; – событие, состоящее в том, что только первое изделие стандартное;
– событие, состоящее в том, что только первое изделие стандартное;  – только второе изделие стандартное. Событие
– только второе изделие стандартное. Событие  можно рассматривать как произведение двух событий
можно рассматривать как произведение двух событий  , т.е. появилось первое событие и не появилось второе.
, т.е. появилось первое событие и не появилось второе. . События
. События  и
и  несовместные, поэтому
несовместные, поэтому .
. , а вероятность противоположного события через
, а вероятность противоположного события через  , то получим
, то получим .
. .
. – событие, состоящее в том, что в первом выбранном поселке находится пункт проката;
– событие, состоящее в том, что в первом выбранном поселке находится пункт проката; 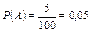 .
.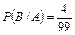 .
. .
. ,
,  события установки на автомашину двигателей, изготовленных соответственно на первом, втором или третьем моторных заводах. Вероятности этих событий таковы:
события установки на автомашину двигателей, изготовленных соответственно на первом, втором или третьем моторных заводах. Вероятности этих событий таковы: ;
;  ;
;  ;
;
 ;
; .
. сломали на три части, выбирая наудачу места разлома. Найти вероятность того, что из получившихся трех частей можно составить треугольник.
сломали на три части, выбирая наудачу места разлома. Найти вероятность того, что из получившихся трех частей можно составить треугольник. . Определить вероятность попадания снаряда в мост, находящийся на этой площади, если длина 200 м и ширина 10 м.
. Определить вероятность попадания снаряда в мост, находящийся на этой площади, если длина 200 м и ширина 10 м. ?
? . Вероятность того, что качество детали окажется отличным, для этих станков соответственно равна: 0,9; 0,8 и 0,7. Какой процент деталей отличного качества выпускает цех в целом?
. Вероятность того, что качество детали окажется отличным, для этих станков соответственно равна: 0,9; 0,8 и 0,7. Какой процент деталей отличного качества выпускает цех в целом?


