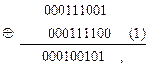Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двійково-десяткові коди з самодоповненням
Необхідність заміни операції віднімання в ЕОМ операцією додавання, що виконується за допомогою спеціальних машинних кодів, привела до розробки ДДК, які мають властивість самодоповнення. В оберненому коді з самодоповненням кожний розряд [ аi ]2 подається як доповнення до 2-1, тобто [ аi ]2 = 2-1 – аi. Доповнення до 2-1=1 дорівнює 0, якщо аі = 1, і 1, якщо аі = 0, тобто є інверсією цифри аi. Для десяткового коду потрібно знаходити доповнення до 9. Зручність цих кодів полягає в тому, що ДДК цифри, яка є доповненням до 9, аналогічно двійковому коду знаходиться простою інверсією двійкових зображень десяткового числа в коді, для якого відшукується доповнення. Таким чином, якщо розряд десяткового числа аi подано тетрадою двійкових розрядів q 4 q 3 q 2 q 1, то доповнення до 9 визначається як [ аі ]10 = Найбільшого поширення з ДДК із самодоповненням дістали код Айкена (2 4 2 1) і код із надмірністю 3 (8 4 2 1), які наведено в табл. 6.4. Як випливає з таблиці, при заміні цифр усіх чотирьох розрядів коду з 0 на 1 (або навпаки) дістаємо доповнення до 9 для кодованої десяткової цифри.
Таблиця 6.4 – Побудова кода Айкена та кода з надмірністю 3
Двійково- шістнадцятковий код У двійково-шістнадцятковому коді для запису двійкового байта (вісім розрядів двійкового коду) використовується шістнадцяткова система числення. При цьому чотирирозрядні двійкові числа (тетради) записуються шістнадцятковим символом. Так, запис двійкових послідовностей 1100 0110, 0010 1101 має вигляд.С6 і.2D, де крапка перед символами вказує на відмінність дворозрядного двійково-шістнадцяткового числа від дворозрядних шістнадцяткових чисел. У цьому прикладі (С6)16 = (198)10 і (2D)16 = (45)10. Двійково-шістнадцятковий код широко застосовується для скороченого запису кодових комбінацій байтової структури. Рефлексні коди Особливість побудови рефлексних кодів полягає в тому, що сусідні кодові комбінації на відміну від двійкових простих кодів різняться цифрою тільки в одному розряді, тобто кодова відстань між ними дорівнює одиниці. Іншою особливістю цих кодів є те, що зміна елементів у кожному розряді при переході від комбінації до комбінації відбувається в два рази рідше, ніж у простому коді, завдяки чому значно спрощується кодер. Крім того, при додаванні двох сусідніх комбінацій рефлексного коду за модулем 2 кількість одиниць дорівнюватиме кількості розрядів мінус 3, тобто одиниці, що використовується для перевірки правильності прийнятої кодової комбінації.
Свою назву рефлексні коди дістали через наявність осей симетрії, відносно яких виразно проглядається ідентичність елементів у деяких розрядах. Вісь симетрії, що розміщується в n -значному рефлексному коді між комбінаціями, які відповідають рівням (2 n -1-1) і 2 n -1, називається головною. Щодо неї є ідентичність елементів в (n -1) розрядах симетричних кодових комбінацій. Можна утворити велику кількість двійкових рефлексних кодів, у яких дві сусідні комбінації відрізнятимуться тільки одним символом (табл. 6.5).
Таблиця 6.5 – Побудова рефлексних кодів
Найбільшого поширення з рефлексних кодів дістав код Грея (табл. 6.6), який, на відміну від інших, простіший при перетворенні його на двійковий простий код. Обернене перетворення двійкового простого коду на код Грея виконується за алгоритмом
де n, починаючи зліва). Таблиця 6.6 – Побудова кода Грея
Таким чином, для утворення комбінації коду Грея практично досить зсунути двійкову комбінацію простого коду на один розряд праворуч, порозрядно додати її за модулем 2 до початкової кодової комбінації без перенесення між розрядами і відкинути молодший розряд здобутої суми. Декодування (обернене перетворення) коду Грея можна виконати двома способами: - перший спосіб
де xn і yn - відповідно значення старшого розряду двійкового простого коду та коду Грея (і = п - 1, п - 2,..., 1, починаючи зліва);
- другий спосіб
де уj - значення розрядів коду Грея, а сума береться за всіма розрядами цього коду від і -годо n -го (старшого, крайнього зліва). Іншими словами, щоб перейти від коду Грея до двійкового простого коду, треба: - залишити цифру старшого розряду без зміни; - кожну наступну цифру інвертувати стільки разів, скільки одиниць є перед нею в коді Грея, або виконати послідовне порозрядне підсумовування за модулем 2 першого (старшого) та другого розрядів комбінації цього коду (1 До характерних особливостей коду Грея належить те, що, по-перше, кожна наступна комбінація завжди відрізняється від попередньої тільки в одній позиції (одному розряді); по-друге, зміна значень елементів у кожному розряді при переході від комбінації до комбінації відбувається в два рази швидше, ніж у двійковому простому коді, тобто якщо в останньому зміна елемента першого (молодшого) розряду відбувається з чергуванням елементів 0-1-0-1-..., елемента другого розряду - з чергуванням елементів 00-11-00-11-..., елемента третього розряду - з чергуванням елементів 0000-1111-0000-1111-... і т. д., то в коді Грея відповідно маємо такі чергування елементів: для першого розряду 11-00-11-00-..., для другого 0000-1111-0000-1111-... і т. д., що дає змогу при тій самій швидкості кодера досягати вищої точності кодування порівняно з двійковим простим кодом; по-третє, при додаванні двох сусідніх комбінацій за модулем 2 кількість одиниць дорівнюватиме кількості розрядів мінус 3, що використовується для перевірки наявності помилки в прийнятій кодовій комбінації; по-четверте, в цьому коді можна виділити кілька осей симетрії, відносно яких спостерігається ідентичність елементів у деяких розрядах. Так, має місце симетрія деяких розрядів відносно осей, проведених між числами 1 і 2, 3 та 4, 5 і 6, 7 та 8, 9 і 10, 11 та 12 (див. табл. 6.6). Код Грея широко застосовується для аналого-цифрового перетворення різних неперервних повідомлень. Він дає змогу зменшити кількість помилок від завад, які виникають при передачі інформації по каналах зв'язку. До недоліків цього коду належить “невагомість” кодової комбінації, коли вага одиниці в ній не визначається номером розряду, на місці якого вона знаходиться, а переведення кодової комбінації з двійкової системи числення в десяткову не визначатиме порядковий номер комбінації в коді Грея. Такі коди важко декодувати, тому перед декодуванням їх, як правило, перетворюють на двійковий простий код, після чого й обробляють останній. Приклад Перетворити на код Грея двійковий простий код 000111001. Розв’язання. Перетворення двійкового простого коду на код Грея виконується за алгоритмом
тобто шукана кодова комбінація має вигляд 000100101.
Коди, що виявляють помилки Особливість кодів, які виявляють помилки, полягає в тому, що кодові комбінації, які входять до складу цих кодів, різняться кодовою відстанню, не меншою ніж dmin = 2.
Такі коди умовно можна поділити на дві групи: коди, в яких використовуються всі комбінації, але до кожної з них за обумовленим правилом додаються r перевірних елементів; коди, утворені зменшенням кількості дозволених комбінацій. До першої групи кодів, що виявляють помилки, належать коди з перевіркою на парність і непарність; код із простим повторенням; інверсний та кореляційний коди; до другої - код зі сталою вагою. Код з кількістю одиниць у комбінації, кратною трьом, може належати до першої або другої групи кодів залежно від методики його побудови.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 625; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.66.151 (0.013 с.) |
 , де
, де  - заперечення двійкової цифри qі.
- заперечення двійкової цифри qі.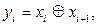
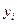 - значення і -го розряду коду Грея;
- значення і -го розряду коду Грея;  ,
,  - відповідні значення розрядів двійкового числа (і =1, 2, …,
- відповідні значення розрядів двійкового числа (і =1, 2, …,

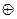 2), після чого послідовно додати 1
2), після чого послідовно додати 1