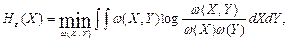Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інформаційні втрати при кодуванні неперервних джерел
Стосовно неперервного джерела на відміну від дискретного можна говорити про нескінченний алфавіт повідомлень, кожне з яких відрізняється від сусідніх на нескінченно малу величину, та нескінченний ансамбль повідомлень. Однак у цьому разі замість імовірностей окремих повідомлень з алфавіту прийнято говорити про диференціальний закон розподілу ймовірностей ω (х) випадкової величини х. Інакше ω (х) називається функцією розподілу густини ймовірностей неперервного повідомлення. При цьому кількість інформації, наявна в прийнятому неперервному повідомленні, як і раніше визначається різницею значень ентропії (невизначеності) джерела повідомлень до та після одержання повідомлення. Нехай густина імовірності ω (х) має вигляд, показаний на рис. 4.1. Проквантуємо за рівнем випадкову величину х із дискретною ∆х. Імовірність того, що хn ≤ х ≤ хп+1, становить р (хi)= ω (хi) ∆х, тобто визначається площею Si, прямокутника:
Рис. 4.1- Розподіл густини імовірності ω (х)
Координату точки хi визначає теорема про середнє. При цьому має виконуватися умова нормування
Ентропія такого штучно утвореного дискретного джерела визначається так, як викладено в пункті 2.3.
Зробимо зворотний перехід до неперервного джерела через спрямування ∆х до 0 та граничний перехід:
оскільки згідно з (4.3)
Друга складова в (4.5) прямує до нескінченності. Отже, ентропія Н (х) неперервного джерела має дорівнювати нескінченності, тобто точне подання випадкового відліку неперервного джерела (одного його повідомлення) потребує нескінченної кількості, скажімо, двійкових розрядів, тому що несе нескінченну кількість інформації. Проте в реальних умовах відлік неперервних повідомлень на приймальному боці виконують у дискретних точках хп , хп+ 1,... (див. рис. 4.6). Це зумовлено скінченною точністю та роздільною здатністю технічних засобів (здатністю їх розрізняти хп і хп+ 1при ∆х → 0). За цих обставин величина ∆х є малою, але має скінченне значення. Таким чином, вираз (4.5) ентропії неперервного джерела має дві складові, одна із яких визначається законом неперервного розподілу ймовірностей, а інша - допустимою точністю (похибкою) ∆х кодування неперервного джерела.
Перша складова
називається диференціальною ентропією,що залежить від статистичних властивостей неперервного джерела. Якщо пронормувати х,щоб зробити цю величину безрозмірною, то можна визначити h (х)у двійкових одиницях (при цьому основа логарифма має дорівнювати двом). Друга складова зовсім не залежить від статистики джерела, Можливий стан джерела повідомлень до одержання повідомлення у на виході каналу визначається розподілом ω (х),а після одержання відліку з неперервного ансамблю у на виході - неперервним законом розподілу умовної імовірності ω (х/y),за яким можна знайти умовну ймовірність, користуючись поняттям елементарної площини ∆х ∆у та роблячи, як і раніше, граничний перехід ∆х → 0, ∆у → 0. Як і в (4.5), загальна умовна ентропія Н (х/у) дорівнює нескінченності, але кількість інформації в цьому відліку, як і раніше, дорівнює різниці безумовної та умовної ентропії джерела відносно виходу каналу, тобто
де ω (х, y) - сумісна щільність імовірності значення відліку у та фактичного значення неперервного повідомлення на виході каналу. Тут h (х), h (х/y) - безумовна й умовна диференціальна ентропія джерела. Друга складова Таким чином, кількість інформації в одному відліку, що передається неперервним каналом, визначається різницею безумовної та умовної диференціальної ентропії неперервного джерела відносно виходу каналу, причому вираз h (х/y)характеризує інформаційні втрати на один відлік при кодуванні неперервного джерела. У теорії вимірювання випадкових величин користуються іншою кількісною мірою інформації - епсилон-ентропією. Припустимо, що випадкова величина У містить інформацію про іншу випадкову величину X - дійсне значення вимірюваної величини, тобто Y є відліком Х упевних одиницях. За цієї умови мінімальна кількість інформації про Х, яка міститься в Y і потрібна для того, щоб за Y відтворити Х із середньоквадратичною похибкою, що не перевищує ε2 (де ε > 0 – наперед задана величина), називається епсилон-ентропією:
При цьому мінімум кількості інформації відшукується за всіма законами розподілу ймовірностей ω (X / Y), тобто
Цю величину, як правило, подають у вигляді
де ω (X, Y) - сумісна щільність розподілу ймовірностей X і Y; ω (X), ω (Y), - одновимірні щільності розподілу цих імовірностей.
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 270; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.153.51 (0.009 с.) |
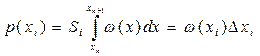 . (4.1)
. (4.1)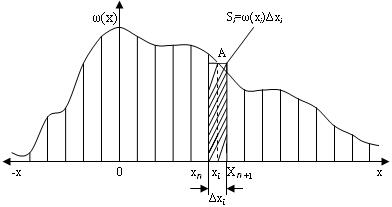
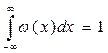 . (4.2)
. (4.2)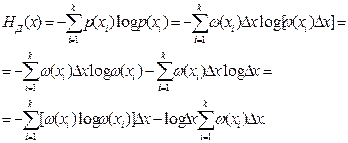 (4.3)
(4.3) (4.4)
(4.4)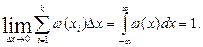
 (4.5)
(4.5)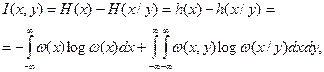 (4.6)
(4.6)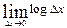 в Н (х) та Н (х/y)виявляється однаковою і при відніманні зникає.
в Н (х) та Н (х/y)виявляється однаковою і при відніманні зникає. .
.