Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Надмірність повідомлень і кодів
Від надмірності повідомлень і кодів, якими вони передаються, залежить максимальна кількість інформації, що може бути передана по каналу за одиницю часу. Розрізняють два види надмірності: природну та штучну. Першою описується надмірність первинних алфавітів, а другою - вторинних. Природна надмірність поділяється на семантичну та статистичну. Семантична надмірність випливає з того, що будь-яку думку, яка міститься в повідомленні, можна висловити коротше. Є багато способів усунення семантичної надмірності: заміною деяких типових повідомлень, які зустрічаються досить часто, умовними позначеннями; введенням таблиць, куди заносяться характерні елементи повідомлення; застосуванням скорочень тощо. Статистична надмірність спричинена нерівномірним розподілом якісних ознак первинного алфавіту та взаємозалежністю їх. Це можна побачити на прикладі англійського алфавіту, що містить 26 літер. Максимальне значення ентропії англійського алфавіту Hmах = 1оg2 q = lоg2 26 = 4,7 біт. Проте у зв'язку з тим, що ймовірність появи літер англійського алфавіту не однакова, ентропія англійської мови значно менша ніж 4,7 біт і без урахування взаємозалежності між словами становить приблизно 2,35 біт. Якщо ж урахувати дійсну частоту появи літер у текстах, різних сполученнях і слів у різних повідомленнях, то інформацію, що передається, можна значно скоротити, стиснути. Коефіцієнт ущільнення інформації визначається виразом K ущ = Н/Н mах, а надмірність - виразом R над = 1 – К ущ = 1 - Н/Н mах. (5.3) Із (5.3) випливає, що для зменшення надмірності повідомлення необхідно збільшити ентропію первинного алфавіту. Для англійської мови R над тобто можна відновити зміст англійських текстів, складених з 50 % алфавіту. До видів статистичної надмірності алфавітів належать такі поняття, як надмірність R над.зв, зумовлена статистичним зв'язком між елементами повідомлення, та надмірність R над.р, спричинена нерівноймовірним розподілом елементів у повідомленні. Надмірність R над.зв вказує на інформаційний резерв повідомлень із взаємозалежними елементами відносно повідомлень, які мають статистичний зв'язок між елементами: R над.зв = 1 - Н/Н ', де Тут Н' теж має надмірність через нерівномірний розподіл імовірностей окремих елементів алфавіту.
Надмірність Н над.рвказує на інформаційний резерв повідомлень, елементи яких нерівноймовірні: R над.р = 1 – Н/Н mах. де Повна статистична надмірність алфавіту визначається виразом R над = R над.зв + R над.р - R над.зв R над.р. При незначних R над.зв і R над.р цей вираз набуває вигляду R над = R над.зв + R над.р, тому що зі зменшенням R над.зв і R над.р добуток їх прямує до нуля. Для усунення статистичної надмірності алфавітів використовують оптимальні нерівномірні коди; при цьому статистична надмірність первинного алфавіту значно зменшується завдяки більш раціональній побудові повідомлень у вторинному алфавіті. Так, при передачі десяткових чисел двійковим кодом трьома двійковими розрядами можна передати і цифру 5, і цифру 8, тобто для передачі п'яти та восьми повідомлень треба мати коди однакової довжини. Довжина комбінації двійкового коду визначається виразом
де N - кількість повідомлень, яку необхідно передати; q 1, q 2 - відповідно якісні ознаки первинного та вторинного алфавітів. Так, для передачі N = 5 повідомлень двійковим кодом (q = 2)потрібно
Загалом надмірність від округлення визначається виразом
де К - округлене до найближчого цілого значення К над = У даному разі
що характеризує недовантаженість коду. Вираз
можна застосувати для визначення довжини кодів з рівноймовірними та взаємонезалежними елементами. Для двійковою коду (q = 2)цей вираз дійсний тільки тоді, коли ймовірність, появи 0 та 1 однакові. Проте в рівномірних кодах, як правило, нулі зустрічаються частіше, ніж одиниці. Тому надмірність, закладену в природу коду, повністю усунути не можна. Однак надмірність від нерівноймовірності появи елемента та надмірність від округлення зменшуються зі збільшенням довжини кодового блока. На відміну від природної надмірності, яка характерна для первинних алфавітів і присутня в повідомленні ще до того, як воно перетворюється на код, штучна надмірність вводиться її нього у вигляді r додаткових елементів спеціально для підвищення його завадостійкості. Таким чином, з п розрядів коду, з яких k несуть інформаційне навантаження, r = п - k розрядів вводяться як коректувальні. Ця величина характеризує абсолютну коректувальну надмірність, а величина
- відносну коректувальну надмірність коду.
Оптимальне кодування У теорії інформації існує кілька методик побудови оптимальних з точки зору швидкості передачі інформації безнадмірних кодів. До оптимальних безнадмірних кодів (з точки зору довжини їх, тобто швидкості передачі інформації) належать нерівномірні коди, які передають повідомлення комбінаціями мінімальної середньої довжини. Оптимальним кодуванням називається процедура перетворення символів первинного алфавіту q 1на кодові комбінації вторинного алфавіту q 2,при якій середня довжина повідомлення у вторинному алфавіті мінімальна. Основним завданням оптимального кодування є досягнення рівності між кількістю інформації І, що виробляється джерелом повідомлень, та обсягом інформації Q на вхо Перша універсальна методика побудови ОНК ґрунтується па методиці Шеннона - Фано і передбачає цю побудову вкодовому алфавіті з кількістю якісних значень q. Згідно з цією методикою виконують такі процедури: 1) множину з N повідомлень, які кодуються, розташовують у порядку спадання ймовірностей; 2) впорядковані за ймовірностями повідомлення розбивають, по можливості, на q рівноймовірних груп; 3) кожній з груп завжди в одній і тій самій послідовності присвоюють символи алфавіту q (всім повідомленням першої групи - першу якісну ознаку цього алфавіту, всім повідомленням другої групи - другу якісну його ознаку тощо); 4) створені групи розбивають, по можливості, на рівноймовірні підгрупи, кількість яких дорівнює або менша ніж q (якщо після розбивання в групі залишається одне повідомлення, то подальший поділ стає неможливим); 5) кожній з утворених підгруп присвоюють якісні ознаки з алфавіту q за процедурою п.3; 6) розбивання та присвоєння ознак алфавіту q повторюють доти, поки після чергового поділу в утворених підгрупах залишиться не більш як одне повідомлення. Друга універсальна методика побудови ОНКґрунтується на відомій методиці Хаффмена. Згідно з цією методикою виконують такі процедури: 1) множину з N повідомлень, що кодуються, розташовують у порядку спадання ймовірностей; 2) останні N 0повідомлень (2 ≤ N 0 ≤ q)об'єднують у нове повідомлення з імовірністю, що дорівнює сумі ймовірностей об'єднуваних повідомлень; 3) утворену множину (N - N 0 + 1) повідомлень розташовують у порядку спадання ймовірностей; 4)об'єднують останні q повідомлень і впорядковують множину повідомлень у порядку спадання ймовірностей. Так діють доти, доки ймовірність чергового об'єднаного повідомлення не дорівнюватиме одиниці; 5) будують кодове дерево, починаючи з кореня, і гілкам цього дерева присвоюють якісні ознаки кодового алфавіту q. Кодові комбінації ОНК - це послідовність якісних ознак, які зустрічаються на шляху від кореня до вершини кодового дерева. Для того щоб перевірити оптимальність коду відносно довжини
Таким чином, утворений код дійсно оптимальний, оскільки n сер < п.
Приклад Побудувати двійковий ОНК Шеннона — Фано і Хаффмена для восьми повідомлень джерела з імовірностями Р (х 1)= 0,3; Р (х2) = 0,2; Р (х 3) = 0,15; Р (х 4)= 0,12; Р (х 5) = 0,1; Р (х 6) = 0,08; Р (х 7) = 0,03; Р (х 8)= 0,02. Розв'язання. Користуючись першою універсальною методикою побудови ОНК, будуємо заданий код (табл. 5.2).
Таблиця 5.2 – Побудова ОНК за першою методикою
Перевіряємо утворений код на оптимальність, для чого визначаємо середню кількість елементів, яка припадає на одну комбінацію коду Шеннона - Фано: n сер= 2(0,3 + 0,2) + 3(0,15 + 0,12 + 0,1) + 4 · 0,08 + 5(0,03 + 0,02) = = 1 + 1,11 + 0,32 + 0,25 = 2,68 < 3, тобто код оптимальний. Користуючись другою універсальною методикою побудови ОНК будуємо заданий код (табл. 5.3).
Таблиця 5.3 – Побудова ОНК за другою методикою
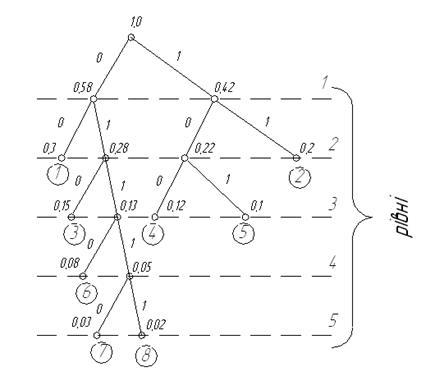
В таблиці використовуємо суму імовірності повідомлення останніх номерів так: 0,03 + 0,02 = 0,05; 0,12 + 0,1 + 0,08 + 0,05 = 0,13; 0,12 + 0,1 = 0,22; 0,22+ + 0,2 = 0,42; 0,58 + 0,42 = 1. Будуємо кодове дерево, що має вигляд, зображений на рис. 5.4.
Рисунок 5.4 – Побудова кодового дерева для утвореного коду
Перевіряємо утворений код на оптимальність, для чого визначаємо середню кількість елементів, яка припадає на одну комбінацію коду Хаффмена: n сер = 2(0,3 + 0,2) + 3(0,15 + 0,12 + 0,1) + 4 · 0,08 + 5 (0,03 + 0,02) = = 1 + 1,11 + 0,32 + 0,25 = 2,68 < З, тобто код оптимальний.
Кодування повідомлень
Повідомлення, що надходять від первісних джерел, як правило, кодуються. Кодування застосовується як для спрощення оброблення повідомлень, так і для підвищення завадостійкості їх передачі по лініях і в каналах зв’язку, де спотворюються сигнали, що спричиняє появу помилок у повідомленнях. Для кодування повідомлень, які надходять з джерела інформації, на першому етапі (первинне оброблення повідомлень) використовуються первинні коди, які мають мінімальну кодову відстань dmin = 1 і не можуть застосовуватися для виявлення та виправлення помилок. Для підвищення завадостійкості передачі повідомлень використовується вторинне кодування комбінацій первинного коду коректувальними кодами, що виявляють і виправляють помилки.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 960; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.227.76 (0.022 с.) |


 .
. або
або 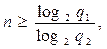
 двійкових символів.
двійкових символів.


 (5.4)
(5.4)

 ді приймача повідомлень.
ді приймача повідомлень.