
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інформаційні втрати при передачі інформації по дискретному каналу
Задача дискретного каналу полягає в тому, щоб повідомлення bi однозначно відповідало повідомленню аi. Це було б можливе тоді, коли р (аi /bi) = р (bi /ai) = 1 для всіх i = 1... К. А це означає, що мають виконуватися рівності р (аi, bi) = р (аi) = р (bi)та р (аi /bj) = р (bj /ai) = 0 або p (аi , bj) = 0 для всіху j ≠ i. Цей випадок стосується каналу з малими завадами, які не можуть спотворити повідомлення аi джерела А так, щоб спостерігач В помилився під час розпізнавання стану джерела В та вибору повідомлення bj. Наведені вище умови означають повний збіг ансамблів А та В (нагадаємо, що до ансамблю входять множина повідомлень і множина імовірностей їх). А якщо це так, то середня кількість переданої інформації на одне повідомлення Н (А)при повній відсутності інформаційних втрат дорівнює такій самій кількості прийнятої інформації Н (В),тобто І (А, В) = Н (А) = H (В) = Н (А, В). (3.6)
Н (А / В) = Н (B / A) = 0. (3.7) Таким чином, кількість переданої інформації за відсутності завад дорівнює ентропії об'єднання джерел А та В або безумовній ентропії одного з них. У разі повної статистичної незалежності джерел А та В,що характеризує високий рівень завад, коли повідомлення bi ніяк статистично незумовлене повідомленням ai, маємо Н (А / В) = Н (А); Н (B / A) = Н (В). (3.8) При цьому ентропія об'єднання двох джерел становитиме Н (А, В) = Н (B, A) = Н (А) + Н (В). (3.9) У разі статистичної незалежності джерел А та В ніяка інформація від А до В через її повне спотворення не передається. Інформаційною мірою цього спотворення є умовна ентропія одного джерела відносно іншого, яка збільшується від нуля згідно з (3.7) до максимуму згідно з (3.8) у міру зростання статистичної зумовленості джерел А та В. У проміжному випадку неабсолютної статистичної залежності джерел А та В завади деякою мірою спотворюють повідомлення, що статистичне відбивається у вигляді матриць імовірностей перехресних переходів. При цьому умовна ентропія має певні рівні: 0 ≤ Н (А / В) ≤ Н (А);0 ≤ Н (B / A) ≤ Н (B). (3.10) Ураховуючи викладене, кількість інформації, що передається в каналі, можна визначити так. Якщо джерело А вибрало певне повідомлення, то воно виробляє кількість інформації, що дорівнює Н (А). Джерело В,вибравши повідомлення
Спостерігач В (приймальний пристрій), вибравши повідомлення I (А, В) = Н (А) - Н (А / В). (3.11) Вираз (3.11) збігається повністю з (3.6) за умови (3.7) при малих завадах і з урахуванням того, що за умови статистичної незалежності (3.8) джерел (великі завади в каналі) I (А, В)= 0. (3.12) Згадаємо, що Н (А, В) = Н (B, A); тому Н (А) + Н (B / A) = Н (В) + Н (A / B). (3.13) Знак рівності тут не зміниться, якщо від обох частин (3.13) відняти суму Н (B / A)+ Н (A / B), тобто Н (А) - Н (A / B) = Н (В) - Н (B / A). (3.14) звідки I (А, В) = I (B, A). (3.15) Таким чином, інформаційні втрати при передачі інформації в каналі визначаються умовною ентропією одного джерела відносно іншого, а кількість переданої інформації - безумовною ентропією джерела та інформаційними втратами за виразом (3.11) або (3.15). З урахуванням (3.11), (3.13) і (3.15) можна записати I (А, В)= Н (А) - Н (A / B) = Н (A) – [ Н (A, B) - Н (B)] = Н (A) + + Н (B) - Н (A, B); I (B, A)= Н (B) - Н (B / A) = Н (B) – [ Н (B, A) - Н (A)] = Н (B) + + Н (A) - Н (B, A); (3.16)
Спостерігається повна симетрія цих виразів.
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 319; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.12.222 (0.019 с.) |

 Остання рівність випливає з того, що за наведених умов
Остання рівність випливає з того, що за наведених умов ,за умови порушення повної статистичної залежності джерел А та В виробляє певну кількість інформації про джерело А,що міститься в джерелі В й дорівнює Н (А / В).
,за умови порушення повної статистичної залежності джерел А та В виробляє певну кількість інформації про джерело А,що міститься в джерелі В й дорівнює Н (А / В).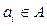 ,яке передавалося, що є одним із його завдань. Прийнявши таке рішення, він виробляє кількість інформації про джерело А, яка дорівнює Н (А). Проте перед цим він уже одержав Н (А / В)бітів інформації про це джерело, тому кількість переданої в каналі інформації про джерело А як кількість нового відсутнього знання визначається різницею
,яке передавалося, що є одним із його завдань. Прийнявши таке рішення, він виробляє кількість інформації про джерело А, яка дорівнює Н (А). Проте перед цим він уже одержав Н (А / В)бітів інформації про це джерело, тому кількість переданої в каналі інформації про джерело А як кількість нового відсутнього знання визначається різницею


