
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрические характеристики сложных сеченийСодержание книги
Поиск на нашем сайте
При вычислении геометрических характеристик сложных сечений последние обычно разбивают на отдельные простые части, геометрические характеристики которых известны (для простых фигур они приведены в справочниках). Из основного свойства интеграла суммы следует, что геометрические характеристики сложной фигуры равны сумме геометрических характеристик её составных частей. Заметим, что в случае, когда в сечении имеется отверстие, его геометрические характеристики необходимо вычитать. Также следует учесть, что суммирование или вычитание геометрических характеристик можно производить только в том случае, если они посчитаны относительно одних и тех же осей. Поэтому, если оси простых фигур не совпадают, предварительно необходимо, используя формулы параллельного переноса (10), пересчитать геометрические характеристики относительно одной и той же оси. Пример. Определить положение главных центральных осей и значения геометрических характеристик относительно них для сложного сечения (рис. 12).
Рис. 12
Разобьем данное сечение на элементарные фигуры, геометрические характеристики которых известны по справочникам. Оси Х1У1 – центральные оси первой фигуры. Оси Х2У2 – центральные оси второй фигуры.
1 фигура – треугольник: F1= Sx1=0 Sy1=0 Ix1= Iy1=
Ix1y1=-
2 фигура – прямоугольник: F2 = bh = 4c∙c = 4c2 Sx2=0 Sy2=0 Ix2= Iy2= Ix2y2=0 Заметим, что центробежный момент инерции прямоугольника равен нулю, т. к. фигура имеет ось симметрии. За вспомогательные оси, относительно которых вычисляем координаты центра тяжести всего сечения, принимаем Х1У1.
Хс= Ус=
По полученным значениям координат центра тяжести находим положение центральных осей всего сечения. Найдем геометрические характеристики всего сечения относительно центральных осей. Так как оси параллельны, воспользуемся формулами преобразования при параллельном переносе осей.
Sxс=0 Syс=0 Ixc = =(1,5с4 + (0,86с)2∙3с2) + (0,33с4 + (-0,64с)2∙4с2) = 5,69с4 Iyc = =(0,67с4 + (-0,76с)2∙3с2) + (5,33с4 + (0,57с)2∙4с2) = 9,03с4 Ixcyc = =(-0,5с4 + (0,86с)∙(-0,76с)∙3с2) + (0 + (-0,64с)∙(0,57с)∙4с2) = -3,92с4
Найдем положение главных центральных осей сечения. Для этого определяем угол поворота центральных осей.
tg2a= a=0,5arctg(- 2,35) = - 33,5°.
Так как получили отрицательный угол, то поворачиваем центральные оси по часовой стрелке. Найдем значения геометрических характеристик относительно главных центральных осей сечения Х0У0:
Iх0= Iхc×cos2a - Iхcуc×sin2a + Iуc×sin2a = 5,69с4 ∙cos2(-33,5) + 3,59c4∙sin(-67) + 9,03с4∙sin2(- 33,5) = 3,4с4; Iу0= Iyc×cos2a + Iхcуc×sin2a + Ixc×sin2a = 9,03с4∙ cos2(-33,5) – 3,59c4∙sin(-67) + 5,69с4∙ sin2(- 33,5) = 11,32с4; Iх0у0= Iхcуc×cos2a - 0,5×sin2a×(Iyc - Ixc) = - 3,92× cos(-67) – 0,5×sin(-67)×(9,03с4 – 5,69с4) = 0.
Статические моменты инерции сечения при повороте осей проходящих через центр тяжести не меняются и остаются равными нулю.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |






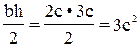

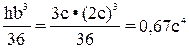



 =
= 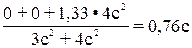
 =
=  - 0,86c
- 0,86c



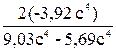 = – 2,35,
= – 2,35,


