
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Касательные напряжения при изгибе. Формула Журавского
Рассмотрим задачу об определении касательных напряжений при изгибе для узкого прямоугольника в качестве сечения. При изгибе Qу ¹0 и Мх ¹0. В этом случае в сечении возникают три напряжения sz, tzx, tzy. Тогда уравнения равновесия (54) и (55) из полной математической модели твердо деформированного тела примут следующий вид:
Из первых двух уравнений следует, что касательные напряжения являются функцией двух переменных (х, у). так как поверхность стержня свободна от напряжений, то по периметру сечения tzx = 0 по закону парности касательных напряжений (рис. 37).
Рис. 37
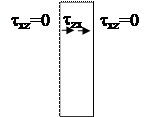
Для узкого прямоугольника они не успевают вырасти, поэтому будем считать tzx равными нулю по всей ширине сечения. Тогда третье уравнение равновесия примет вид:
По той же причине, что прямоугольник узкий, будем считать, что tzy по ширине сечения при у = const распределено равномерно и является функцией только координаты у:
Пользуясь формулой нормальных напряжений в поперечном сечении (28), при изгибе получим:
s =
Мх’ = Qy
Проинтегрировав полученное выражение, получим:
tzy=-
Постоянную интегрирования можно определить из условия равенства нулю касательного напряжения tzy при у=
С = -
Подставив значение константы в выражение (82) получим:
tzy=-
На основе выражения в скобках можно сделать вывод, что касательные напряжения в сечении распределены по параболе.
Рис. 38
Преобразуем выражение в скобках:
На рис. 38 координатой y отсекается заштрихованная часть, которая имеет площадь F*=
tzy=
Эта формула носит название формулы Журавского и служит для определения касательных напряжений, возникающих в сечении при изгибе.
Теории (гипотезы) прочности
Важнейшей задачей инженерного расчета является оценка прочности детали по известному напряженному состоянию, т.е. по известным главным напряжениям в каждой точке тела.
Наиболее просто эта задача решается при простых видах деформации, в частности, при одноосных напряженных состояниях, т.к. в этом случае экспериментально легко установить значение предельных (опасных) напряжений. Под последними понимают напряжения, соответствующие началу разрушения (при хрупком состоянии материала) или появлению остаточных деформаций (в случае пластического состояния материала). Так, испытания образцов из определённого материала на простое растяжение или сжатие позволяют без особых трудностей определить значение опасных напряжений:
sо = sв – временное сопротивление.
По опасным напряжениям устанавливают допускаемые при растяжении [s+] или сжатии [s-] напряжения, обеспечивая коэффициент запаса против наступления предельного состояния. Таким образом, условие прочности при одноосном напряженном состоянии принимает вид:
s1£[s+], |s3|£ [s+].
Рассмотрим теперь вопрос о прочности материала при сложном напряженном состоянии, когда в точках детали два или все три главных напряжения s1, s2, s3 не равны нулю. В этих случаях, как показывают опыты, для одного и того же материала опасное состояние может иметь место при различных предельных значениях главных напряжений в зависимости от соотношений между ними. Поэтому экспериментально установить предельные величины главных напряжений очень сложно не только из-за трудности постановки опытов, но и из-за большого объема испытаний. Другой путь решения задачи заключается в установлении критерия прочности (критерия предельного напряженно-деформированного состояния). Для этого вводят гипотезу о преимущественном влиянии на прочность материала того или иного фактора: полагают, что нарушение прочности материала при любом напряженном состоянии наступит только тогда, когда величина данного фактора достигнет некоторого предельного значения. Предельное значение фактора, определяющего прочность, находят на основании простых, легко осуществимых опытов на растяжение. Иногда пользуются также результатами опытов на кручение. Таким образом, введение критерия прочности позволяет сопоставлять данное сложное напряженное состояние с простым, например, с одноосным растяжением, и установить при этом такое эквивалентное (расчётное) напряжение, которое в обоих случаях дает одинаковый коэффициент запаса.
Под коэффициентом запаса в общем случае напряженного состояния понимают число n, показывающее, во сколько раз нужно одновременно увеличить все компоненты напряженного состояния s1, s2, s3, чтобы оно стало предельным. В настоящее время разработано достаточно большое число гипотез прочности. Ниже рассмотрим некоторые из них.
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 208; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.70.101 (0.008 с.) |
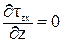
 ,
,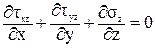 .
.
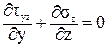 . (81)
. (81)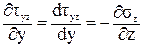 .
. ,
,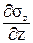 =
= 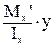 ,
,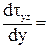
 .
. ×
× 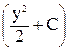 . (82)
. (82)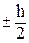 :
: =0,
=0, .
. =
= 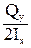 ×
× 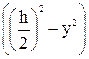 . (83)
. (83)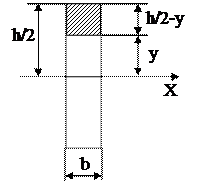
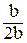 =
= 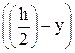 ×
× 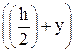 ×
× 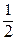 . Произведение площади фигуры на координату ее центра тяжести относительно какой-либо оси дает статический момент инерции Sx*. Таким образом, выражение (83) примет вид:
. Произведение площади фигуры на координату ее центра тяжести относительно какой-либо оси дает статический момент инерции Sx*. Таким образом, выражение (83) примет вид: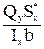 . (84)
. (84) sт – предел текучести
sт – предел текучести


