
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физическая и математическая модельСтр 1 из 9Следующая ⇒
Физическая и математическая модель
Физическая модель – упрощенное представление объекта или явления, сохраняющая основные его черты. Применительно к расчетам на прочность и жесткость физическая модель должна отражать: геометрические свойства детали, свойства материала детали, действующие на деталь нагрузки. По геометрическим признакам все тела делятся на три группы: 1. стержни – тела, у которых одно измерение существенно больше двух других (характеризуются поперечным сечением и формой оси). 2. пластины и оболочки – тела, у которых одно измерение существенно меньше двух других (характеризуются толщиной и формой серединной поверхности). 3. массивы – тела, у которых все три измерения соизмеримы. Реальные конструкционные материалы (стали, чугуны, цветные материалы) имеют кристаллическое строение; кристаллы малы и расположены хаотично. Сложность реального строения и возникающая трудность при математическом его описании явились причиной разработки модели твердого тела. Эта модель должна сохранить основные свойства материалов и в тоже время сделать простым их аналитическое описание. Поэтому в расчетах на прочность и жесткость принимается ряд основных гипотез и допущений: 1. сплошность – материал не имеет в своей структуре пустот. 2. однородность – одинаковые свойства материала в любой точке детали. 3. изотропность – одинаковые свойства материала в различных направлениях. 4. идеальная упругость (упругость – свойство тела восстанавливать форму и размеры после снятия нагрузки; пластичность – свойство тела получать большие остаточные деформации после снятия нагрузки). 5. отсутствие первоначальных внутренних напряжений. 6. принцип малых перемещений – перемещения конструкции малы по сравнению с размерами конструкции. 7. линейная деформируемость материала – в зоне действия упругих деформаций зависимость между силой и приращением размера линейная. 8. гипотеза плоских сечений – плоское до нагружения сечение остается плоским и после нагружения. Все свойства физической модели, описанные уравнениями, составляют математическую модель деформированного тела. Математическая модель должна содержать три группы уравнений: 1) Статические – включающие нагрузки и условия равновесия;
2) Физические – отражающие связь между нагрузками и деформациями; 3) Геометрические – отражающие изменение формы и размеров под нагрузкой.
Экстремальные свойства главных напряжений. Круговая диаграмма Мора
Возьмем в теле произвольную точку А (х, у, z). Через эту точку можно провести бесконечное множество площадок. Очевидно, что на одной из площадок нормальное напряжение достигнет наибольшего для данной точки значения, а на другой касательное напряжение примет свое максимальное значение. Пусть для точки А известно положение главных осей напряженного состояния. Если их принять за систему координат (рис. 23), то в наклонной площадке с вектором нормали n (l, m, n) возникают нормальные и касательные напряжения Р(s, t). Определим эти напряжения и исследуем их экстремальные свойства.
Рис. 23
Нормальные напряжения в любой наклонной площадке выражаются основной квадратичной формой (33). Запишем её с учетом того, что в качестве системы координат приняты главные оси:
sn = s1×l2 + s2×m2 + s3×n2. (38)
Найдем квадрат полного напряжения на наклонной площадке как сумму квадратов его проекций, выражения для которых были найдены ранее (32):
Р2 = Pх2+ Pу2 + Pz2 = s12×l2 + s22×m2 + s32×n2. (39)
Также полное напряжение на наклонной площадке можно представить как сумму нормального и касательного напряжений (17). Таким образом, мы имеем систему трех уравнений с тремя неизвестными - l2, m2, n2:
s2 + t2 = s12×l2 + s22×m2 + s32×n2 (40) 1 = l2 + m2 + n2
Умножим каждое уравнение на произвольные множители a, b, c и сложим, сгруппировав при этом слагаемые по направляющим косинусам
а×s + b×(s2 + t2) + с = = l2×(а×s1 + b×s12 + с) + m 2×(а×s2 + b×s22 + с) + n 2×(а×s3 + b×s32 + с). (41)
Для определения величины l2 подберем коэффициенты a, b, c таким образом, чтобы вторая и третья скобки в правой части уравнения (41) обнулились:
а×s2 + b×s22 + с = 0, а×s3 + b×s32 + с = 0, получаем
b = 1, а = -(s2 +s3), с = s2×s3.
Подставляя полученные коэффициенты в уравнение (41), находим величину l2:
l2=
Аналогично находим квадраты двух других направляющих косинусов
m 2 = (43) n 2 =
В уравнениях (42) и (43) дроби должны быть больше нуля, т.к. в левых частях стоят квадраты величин. Проанализируем знаменатели дробей на основе неравенства s1 ³ s2 ³ s3:
На основе неравенств (44) можно сделать вывод о знаке числителя:
Сделав ряд математических преобразований, можно показать, что неравенства (45) представляют собой области, ограниченные окружностями. Рассмотрим третье неравенство и представим его решение графически (рис. 24):
Представим решение системы (45) графически (рис. 25). Эта диаграмма называется круговой диаграммой Мора. Круговая диаграмма позволяет установить экстремальные свойства нормальных и касательных напряжений.
Рис. 24
s1 – максимальное нормальное напряжение, которое может возникнуть в точке на любой наклонной площадке; s3 – минимальное нормальное напряжение, которое может возникнуть в точке на любой наклонной площадке; tmax =
Рис. 25 Теории (гипотезы) прочности
Важнейшей задачей инженерного расчета является оценка прочности детали по известному напряженному состоянию, т.е. по известным главным напряжениям в каждой точке тела. Наиболее просто эта задача решается при простых видах деформации, в частности, при одноосных напряженных состояниях, т.к. в этом случае экспериментально легко установить значение предельных (опасных) напряжений. Под последними понимают напряжения, соответствующие началу разрушения (при хрупком состоянии материала) или появлению остаточных деформаций (в случае пластического состояния материала). Так, испытания образцов из определённого материала на простое растяжение или сжатие позволяют без особых трудностей определить значение опасных напряжений:
sо = sв – временное сопротивление.
По опасным напряжениям устанавливают допускаемые при растяжении [s+] или сжатии [s-] напряжения, обеспечивая коэффициент запаса против наступления предельного состояния. Таким образом, условие прочности при одноосном напряженном состоянии принимает вид:
s1£[s+], |s3|£ [s+].
Рассмотрим теперь вопрос о прочности материала при сложном напряженном состоянии, когда в точках детали два или все три главных напряжения s1, s2, s3 не равны нулю. В этих случаях, как показывают опыты, для одного и того же материала опасное состояние может иметь место при различных предельных значениях главных напряжений в зависимости от соотношений между ними. Поэтому экспериментально установить предельные величины главных напряжений очень сложно не только из-за трудности постановки опытов, но и из-за большого объема испытаний. Другой путь решения задачи заключается в установлении критерия прочности (критерия предельного напряженно-деформированного состояния). Для этого вводят гипотезу о преимущественном влиянии на прочность материала того или иного фактора: полагают, что нарушение прочности материала при любом напряженном состоянии наступит только тогда, когда величина данного фактора достигнет некоторого предельного значения. Предельное значение фактора, определяющего прочность, находят на основании простых, легко осуществимых опытов на растяжение. Иногда пользуются также результатами опытов на кручение. Таким образом, введение критерия прочности позволяет сопоставлять данное сложное напряженное состояние с простым, например, с одноосным растяжением, и установить при этом такое эквивалентное (расчётное) напряжение, которое в обоих случаях дает одинаковый коэффициент запаса.
Под коэффициентом запаса в общем случае напряженного состояния понимают число n, показывающее, во сколько раз нужно одновременно увеличить все компоненты напряженного состояния s1, s2, s3, чтобы оно стало предельным. В настоящее время разработано достаточно большое число гипотез прочности. Ниже рассмотрим некоторые из них. Пример Для заданной схемы нагружения стержня (рис. 43) построить эпюру продольной силы N(z) при следующих исходных данных: q=10 кН/м, l=1м.
Рис. 43
Решение 1. Совместим начало системы координат с левым концом стержня и направим координатную ось z вдоль его продольной оси. В соответствии со схемой нагружения разделим стержень на три участка и запишем уравнение продольных сил следующим образом:
N (z) = N (0) - 2q·z│1+2q (z - l) │2 + q (z - 2l) │3.
В этом уравнении приняты следующие обозначения: N(0) – значение продольной силы в начале координат (реакция опоры), z – координата сечения, в котором определяется значение продольной силы. Для решения задачи необходимо определить одну неизвестную величину – N(0). Для этого запишем граничное условие: N (3l) = 0. Напомним, что граничные условия – это известные значения интегральных характеристик в какой-либо точке стержня. Для определения неизвестной реакции N(0) необходимо приравнять уравнение продольных сил к нулю, подставив в нем вместо координаты «z» координату «3l»:
N (0)-2q (3l) + 2q (3l – l) + q (3l – 2l) = 0. Решая это уравнение, найдем: N (0) = 10 кН. 2. Построение графика продольных сил. При построении графиков уравнение рассматривается на каждом участке в отдельности и вместо координаты «z» подставляется соответствующая координата начала и конца рассматриваемого участка.
1 участок - 0 ≤ z ≤ l:
N (0) =10 кН, N (l) = 10 – 2·10·1 = -10 кН.
2 участок - l ≤ z ≤ 2l:
N (l) = 10 – 2·10·1 + 2·10(l – l) = -10 кН, N (2l) = 10 – 2·10·2 + 2·10(2 – 1) = -10 кН.
3 участок - 2l ≤ z ≤ 3l:
N (2l) = 10 – 2·10·2 + 2·10(2 – 1) + 10(2 – 2) = -10 кН, N (3l) = 10 – 2·10·3 + 2·10(3 – 1) + 10(3 – 2) = 0 кН.
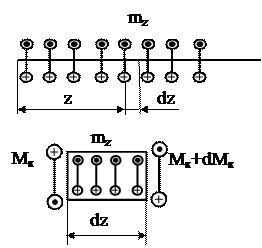
По рассчитанным значениям строится график продольной силы (см. рис. 43). Кручение стержней Пусть стержень нагружен произвольной крутящей нагрузкой. Вырежем на некотором расстоянии z бесконечно малый элемент dz (рис. 44). На данный элемент действует внешняя нагрузка и внутренние крутящие моменты в сечениях, по которым вырезан элемент. Составим уравнение равновесия вырезанного элемента.
- Мк + mz×dz + Мк + dМк = 0,
Мк’ + mz = 0. (94)
Рис.44
Решение данного дифференциального уравнения с правой частью состоит из двух частей общего и частного решения и имеет вид
Mк(z) = C -
Определим физический смысл постоянной интегрирования. При z=0
Мк(0) = C.
Значение интеграла зависит от внешней приложенной нагрузки. Рассмотрим значения нагрузочных функций для наиболее часто встречающихся нагрузок. а) сосредоточенный момент (рис. 44):
Рис.44 при z£a Фм(z)=0 при z³a Фм(z)=-L
 б) распределенная нагрузка (рис. 45): б) распределенная нагрузка (рис. 45):
Рис. 45
при z£c Фм(z)=0 при z³c Фм(z)=-m(z-c)
Пример Для приведённой схемы нагружения прямого стержня (рис. 46) построить эпюру крутящего момента при следующих исходных данных: mz = 10 кН/м, L = 10 кНм, l = 1 м. Решение В соответствии со схемой нагружения запишем уравнение крутящего момента в следующем виде: Mk (z) = Mk (0) │1 - L│2 - mz(z-2l) │3 .
Исходя из условий закрепления стержня, запишем следующее граничное условие: Mk (0) = 0 (реакция незакреплённого конца стержня равна нулю).
Рис. 46
Таким образом, записанное уравнение не содержит неизвестных величин и можно приступать к построению графика. Построение графика будем производить аналогично построению графика в примере 1.
1 участок - 0 ≤ z ≤ l: Mk (0) = 0 кНм, Mk (l) = 0 кНм.
2 участок - l ≤ z ≤ 2l: Mk (l) = 0 – 10 = -10 кНм, Mk (2l) = 0 – 10 = -10 кНм.
3 участок - 2l ≤ z ≤ 3l: Mk (2l) = 0 – 10 – 10(2 – 2) = - 10 кНм, Mk (3l) = 0 – 10 – 10(3 – 2) = -20 кНм.
По рассчитанным значениям строится график крутящего момента (см. рис. 46).
Изгиб стержней
Пусть стержень нагружен произвольной поперечной нагрузкой. Вырежем на некотором расстоянии z бесконечно малый элемент dz (рис. 47). На данный элемент действует внешняя нагрузка и внутренние поперечные силы и изгибающие моменты в сечениях, по которым вырезан элемент.
Рис. 47
Составим уравнения равновесия вырезанного элемента. Уравнение равновесия всех сил на вертикальную ось.
- Qy + qy×dz + Qy + dQy = 0,
Qy' + qy = 0. (96)
Уравнение равновесия моментов относительно центра тяжести правого сечения вырезанного элемента.
- Мх + qy×dz×dz/2 + Мх + dМх - Qy×dz = 0,
Слагаемое, выражающее момент от распределенной нагрузки – слагаемое второго порядка малости, поэтому им можно пренебречь
Мх' = Qy. (97)
Объединяя дифференциальные уравнения (96) и (97), получим:
Мх'' = - qy (98)
Решение данного дифференциального уравнения с правой частью состоит из двух частей общего и частного решения и имеет вид
Мх(z) = C1+С2z – Фм,
где Фм – частное решение, отражающее внешнюю приложенную нагрузку. Определим физический смысл постоянных интегрирования. При z=0
Мх(0) = C1, Мх' (0) = Qy(0) = С2.
Рассмотрим подробнее частное решение. Пусть стержень нагружен произвольной распределенной нагрузкой (рис. 48). Определим величину поперечной силы и изгибающего момента для точки с координатой z.
Рис. 48
Qy = Мх =
Значения интегралов зависят от внешней приложенной нагрузки. Рассмотрим значения нагрузочных функций для наиболее часто встречающихся нагрузок. а) сосредоточенная сила (рис. 49):
Рис. 49 при z£a ФQ(z)=0 ФМ(z)=0 при z³a ФQ(z)=-P ФМ(z)=-P(z-a)
б) распределенная нагрузка (рис. 50):
Рис. 50 при z£c ФQ(z)=0 ФМ(z)=0 при z³c ФQ(z)=-q(z-c) ФМ(z)=-q(z-c)2/2 в) сосредоточенный момент (рис. 51):
Рис. 51 при z£b ФQ(z)=0 ФМ(z)=0 при z³b ФQ(z)=0 ФМ(z)=-L Пример Для заданной схемы нагружения стержня (рис. 52) построить эпюры поперечной силы Qy(z) и изгибающего момента Mx(z) при следующих исходных данных: L = 5 кНм, P = 10 кН, q = 20 кН/м, l = 1 м.
Рис. 52 Решение Запишем уравнения поперечных сил и изгибающего момента:
Qy (z) = Qy(0) │1 – P - q×(z - l) │2 Mx (z) = Mx (0) + Qy(0)×z│1 - P×(z - l) - q×(z - l)2/2│2
В соответствии с условиями закрепления стержня запишем граничные условия в следующем виде: Mx (0) = - L, Mx (3l) = 0. Для нахождения неизвестной реакции Qy (0) необходимо приравнять уравнение изгибающего момента к нулю при координате z = 3l:
Mx (3l) = Mx (0) + Qy (0)×3l - P×(3l - l) - q×(3l - l)2/2 = 0.
Решая это уравнение относительно Qy (0), получим Qy (0) = 21.67кН. Теперь, учитывая найденные константы, уравнения интегральных характеристик можно переписать в следующем виде:
Qy (z) = 21.67│1 – P – q×(z - l) │2 Mx (z) = -L + 21.67z│1 – P×(z - l) – q×(z - l)2/2│2
Построение графиков будем производить аналогично примеру 1.
1 участок 0 ≤ z ≤ l: Qy (0) = 21.67 кН, Qy (l) = 21.67 кН, Mx (0) = -5 кНм, Mx (l) = -5 + 21.67*1 = 16.67 кНм.
2 участок l ≤ z ≤ 3l: Qy (l) = 21.67 – 10 = 11.67 кН, Qy (3l) = 21.67 – 10 – 20*(3 - 1) = -28.33 кН, Mx (l) = -5 + 21.67*1 – 10(1 – 1) – 20(1 – 1) = 16.67 кНм, Mx (3l) = -5 + 21.67*3 – 10(3 – 1) – 20(3 – 1) =0 кНм.
Определим координаты экстремума и значения функции изгибающего момента в экстремальной точке:
Qy (z1) = 21.67 – P – q (z1 - l) = 0 → z1 = 1.58 м. Mx (1.58) = -L + 21.67·1.58 – P (1.58 - l) – q (1.58 - l)2/2 = 20.07 кНм.
По рассчитанным значениям строятся графики поперечной силы и изгибающего момента (см. рис. 52).
Физическая и математическая модель
Физическая модель – упрощенное представление объекта или явления, сохраняющая основные его черты. Применительно к расчетам на прочность и жесткость физическая модель должна отражать: геометрические свойства детали, свойства материала детали, действующие на деталь нагрузки. По геометрическим признакам все тела делятся на три группы: 1. стержни – тела, у которых одно измерение существенно больше двух других (характеризуются поперечным сечением и формой оси). 2. пластины и оболочки – тела, у которых одно измерение существенно меньше двух других (характеризуются толщиной и формой серединной поверхности). 3. массивы – тела, у которых все три измерения соизмеримы. Реальные конструкционные материалы (стали, чугуны, цветные материалы) имеют кристаллическое строение; кристаллы малы и расположены хаотично. Сложность реального строения и возникающая трудность при математическом его описании явились причиной разработки модели твердого тела. Эта модель должна сохранить основные свойства материалов и в тоже время сделать простым их аналитическое описание. Поэтому в расчетах на прочность и жесткость принимается ряд основных гипотез и допущений: 1. сплошность – материал не имеет в своей структуре пустот. 2. однородность – одинаковые свойства материала в любой точке детали. 3. изотропность – одинаковые свойства материала в различных направлениях. 4. идеальная упругость (упругость – свойство тела восстанавливать форму и размеры после снятия нагрузки; пластичность – свойство тела получать большие остаточные деформации после снятия нагрузки). 5. отсутствие первоначальных внутренних напряжений. 6. принцип малых перемещений – перемещения конструкции малы по сравнению с размерами конструкции. 7. линейная деформируемость материала – в зоне действия упругих деформаций зависимость между силой и приращением размера линейная. 8. гипотеза плоских сечений – плоское до нагружения сечение остается плоским и после нагружения. Все свойства физической модели, описанные уравнениями, составляют математическую модель деформированного тела. Математическая модель должна содержать три группы уравнений: 1) Статические – включающие нагрузки и условия равновесия; 2) Физические – отражающие связь между нагрузками и деформациями; 3) Геометрические – отражающие изменение формы и размеров под нагрузкой.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.153.38 (0.158 с.) |

 s = s1×l2 + s2×m2 + s3×n2
s = s1×l2 + s2×m2 + s3×n2 . (42)
. (42) ,
, .
. ³ 0,
³ 0, £ 0, (44)
£ 0, (44) ³ 0.
³ 0.
 ³ 0,
³ 0, £ 0, (45)
£ 0, (45) ³ 0.
³ 0. (46)
(46)
 – максимальное касательное напряжение, которое может возникнуть в точке на любой наклонной площадке, действует на площадках наклоненных к главным на угол 45°.
– максимальное касательное напряжение, которое может возникнуть в точке на любой наклонной площадке, действует на площадках наклоненных к главным на угол 45°.
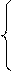 sт – предел текучести
sт – предел текучести
 ,
,
 . (95)
. (95)
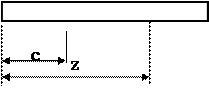



 ,
, ,
,
 ,
, . (99)
. (99)






