
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание синтаксиса. Нормальная форма Бэкуса-Наура (БНФ).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Описание синтаксиса. Нормальная форма Бэкуса-Наура (БНФ). Это способ описания синтаксического языка. Это металингвистическая формула для описания конструкций языка программирования. Металингвистическая формула для языка модельного программирования ML. <программа>::=<оператор>.|<оператор>;<программа> (слева та конструкция, которую мы определяем, справа метапеременные, символы языка, после.|). Металингвистическая формула содержит метапеременные, обозначающие соответственную конструкцию языка. Метапеременные заключаются <>, БНФ это название конструкции языка, например, <программа>,<оператор>. Наша формула означает: <программа> 1) <оператор>. 2) <оператор>;<оператор>. 3) ………………………. -программа может состоять из 1-го оператора, из 2-х и нескольких операторов. Определим, что такое <оператор>: <оператор>::=<присваивание>|<условный>|<цикл>|<составной> <присваивание>::=<идентификатор>:=<выражение> <условный>::=if <логическое> then <оператор> else <оператор> <цикл>::=while <логическое> do <оператор> <составной>::=begin <программа> end (или «.») <идентификатор> - логическая единица. <выражение>::=<терм>|<выражение>+<терм>|<выражение>-<терм> <терм>::=<множитель>|<терм>*<множитель>|<терм>/<множитель> <множитель>::=<идентификатор>|<const>|(<выражение>) <логическое>::=<выражение><знак сравнения><выражение> <знак сравнения>::=<|>|<=|>=|=|<> <const> - логическая единица. Грамматики Хомского.
G(V,T,P,б) V-нетерминальный алфавит (метапеременная). T-терминальный алфавит (символы языка). P-правила вывода (формулы БНФ). б-начальный символ грамматики (<программа>). б?V P (L→B); B?(VvT)*; L?(VvT)*·V·(VvT)*; *-любая строчка, построенная над алфавитом; А-алфавит (любое конечное множество А);
Все операции теории множеств можно производить над алфавитами, т.к. являются элементами множества. A·B={ab,a?A,b?B} A²=A·A
Грамматики Хомского называется: Уровни 1. 1. НС – непосредственно составляющих или КЗ – контекстно зависимых. Если для каждого правила грамматики соответствует условие:
-под знаком || понимаем длину строки. Если одно название грамматики – неукорачивающаяся. Уровни 2. 2.Контекстно свободные грамматики – Если каждое правило обладает свойством:
(левая часть правила является единственным нетерминальным символом, т.е. не строкой). Уровни 3. 3.Линейные – Если каждое правило имеет следующий вид: X→ay,X→a (праволинейная, нетерминал справа) X→yа,X→a (леволинейная, нетерминал слева) X,y?V a?T* x,y – нетерминальные символы; а - строка терминальных символов.
Синтаксическое дерево. Это графическое изображение всех выводов в данной цепочке символов, в данной грамматике. Вершиной синтаксического дерева является начальный символ грамматики.
M If WH
C
Листья – терминальные символы.
Если вершина дерева является нетерминалом, то ее дочерними вершинами будут элементы правой части правила, используемого при выводе данной цепочки.
Синтаксический анализ. .б (вершина)
(набор листьев) Существуют нисходящий и восходящий анализы. Нисходящий анализ – заключается в том, что, начиная с вершины дерева, последовательно строим дочерние вершины до тех пор, пока они не соединятся с листьями. Восходящий анализ - заключается в том, что здесь построение начинается с листьев. В соответствии с правилами грамматики осуществляется свертка до тех пор, пока они все не соединятся с вершиной.
Интерпретирующая семантика. Компилирующая семантика. Интерпретирующая семантика – это некоторая функция, которая любую программу/набор данных отображает в виде результата:
Компилирующая семантика:
Интерпретирующую семантику задает интерпретатор.
ПОЛИЗ(польс.инверсная запись) Триады Системы внутреннего Ассемблер представления
Таблица символов.
Память Представления программ. Триады – набор из 5 операций:
Последовательность триад
Kon – код операции; C:=a+b -*/v& 1-й,3-й не используются, а в «b» стоит метка N.
Входной язык Выходной язык (вводим на входе) (получаем на выход.яз.)
Это перевод с одного формального языка на другой формальный язык.
Типы перевода: 1. Гомоморфизм – некоторое отображение, сохраняющее алгебраическую операцию.
В нашем случае конкатенацию.
Вх.строка вых.строка
2. Схемы синтаксически управляемого переводов. (СУ схемы).
Входной язык задается контекстно-свободной грамматикой, т.е. есть набор правил. Этот набор считается входным. Каждому входному правилу добавляется еще одно выходное.
Входное правило Выходное правило E→T T E→E+T ET+ T→M M T→T*M TM* M→a a M→(E) E
Это СУ схема с 2-мя правилами: входное и выходное.
Пример, как работает эта схема:
T T
() M C
E T E +
T M T M
M b M b
a a
Как хранится у нас это входное дерево:
E→T E→T T→T*M T→TM* T→M T→M M→(E) M→E E→E+T E→ET+ E→T E→T T→M T→M M→a M→a T→M T→M M→b M→b M→c M→c
Эта схема называется простой схемой СУ перевода. Простые СУ переводы – это подкласс СУ перевода. Особенностью простых СУ схем является то, что в выходном правиле нетерминалы следуют в том же порядке, что и во входном.
Схема перевода в триады.
Assembler
Содержание: Синтаксис языков программирования. Описание синтаксиса. Нормальная форма Бэкуса-Наура (БНФ) стр.1 Грамматики Хомского стр.2 Описание языка ML посредствам правил КС – грамматики стр.3 Синтаксическое дерево стр.5 Нисходящий синтаксический анализатор с возвратом стр.6 Нисходящий анализатор без возвратов (LL(1)) стр.8 Грамматика ML для правила LL(1) стр.9 Алгоритм рекурсивного спуска стр.10 Семантика языков программирования стр.12 Семантика лексических единиц стр.13 Формальные системы для внутреннего (промежуточного) стр.13 представления программ Системы перевода формальных языков стр.14 Языки характеризующего перевода стр.15 Схема перевода в полиз для нашего языка ML стр.17 без переходов Схема перевода в полиз с переходами стр.17 Схема перевода в триады стр.18 Assembler стр.20
Описание синтаксиса. Нормальная форма Бэкуса-Наура (БНФ). Это способ описания синтаксического языка. Это металингвистическая формула для описания конструкций языка программирования. Металингвистическая формула для языка модельного программирования ML. <программа>::=<оператор>.|<оператор>;<программа> (слева та конструкция, которую мы определяем, справа метапеременные, символы языка, после.|). Металингвистическая формула содержит метапеременные, обозначающие соответственную конструкцию языка. Метапеременные заключаются <>, БНФ это название конструкции языка, например, <программа>,<оператор>. Наша формула означает: <программа> 1) <оператор>. 2) <оператор>;<оператор>. 3) ………………………. -программа может состоять из 1-го оператора, из 2-х и нескольких операторов. Определим, что такое <оператор>: <оператор>::=<присваивание>|<условный>|<цикл>|<составной> <присваивание>::=<идентификатор>:=<выражение> <условный>::=if <логическое> then <оператор> else <оператор> <цикл>::=while <логическое> do <оператор> <составной>::=begin <программа> end (или «.») <идентификатор> - логическая единица. <выражение>::=<терм>|<выражение>+<терм>|<выражение>-<терм> <терм>::=<множитель>|<терм>*<множитель>|<терм>/<множитель> <множитель>::=<идентификатор>|<const>|(<выражение>) <логическое>::=<выражение><знак сравнения><выражение> <знак сравнения>::=<|>|<=|>=|=|<> <const> - логическая единица. Грамматики Хомского.
G(V,T,P,б) V-нетерминальный алфавит (метапеременная). T-терминальный алфавит (символы языка). P-правила вывода (формулы БНФ). б-начальный символ грамматики (<программа>). б?V P (L→B); B?(VvT)*; L?(VvT)*·V·(VvT)*; *-любая строчка, построенная над алфавитом; А-алфавит (любое конечное множество А);
Все операции теории множеств можно производить над алфавитами, т.к. являются элементами множества. A·B={ab,a?A,b?B} A²=A·A
Грамматики Хомского называется: Уровни 1. 1. НС – непосредственно составляющих или КЗ – контекстно зависимых. Если для каждого правила грамматики соответствует условие:
-под знаком || понимаем длину строки. Если одно название грамматики – неукорачивающаяся. Уровни 2. 2.Контекстно свободные грамматики – Если каждое правило обладает свойством:
(левая часть правила является единственным нетерминальным символом, т.е. не строкой). Уровни 3. 3.Линейные – Если каждое правило имеет следующий вид: X→ay,X→a (праволинейная, нетерминал справа) X→yа,X→a (леволинейная, нетерминал слева) X,y?V a?T* x,y – нетерминальные символы; а - строка терминальных символов.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 565; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.253.224 (0.009 с.) |



 -множество всех строк длины «n» над алфавитом А.
-множество всех строк длины «n» над алфавитом А. -множество всех не пустых строк любой не пустой строки.
-множество всех не пустых строк любой не пустой строки. -множество всех строк над А, включая пустую строку.
-множество всех строк над А, включая пустую строку.



 P
P

 A S P
A S P Id
Id
 := E; S; P
:= E; S; P a P.
a P.
 T A S; S
T A S; S ..
..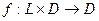



 .
.
 .
.

 .
.



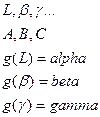


 E E
E E



 T * M T M *
T * M T M *
 M C
M C



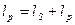


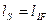


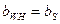







 =Образ (Ген)
=Образ (Ген)




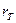 =Образ (Ген)
=Образ (Ген)
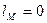
 =Образ (Id)
=Образ (Id)









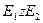


 =Образ
(Ген)
=Образ
(Ген)



 b1
S1
b1
S1


 L
L

















