Метод Гаусса для исследования и решения С.Л.А.У.

Матричный метод и правило Крамера обладают двумя существенными недостатками. Во–первых, они применимы только для систем с невырожденной квадратной матрицей и не работают в случае, когда D=0. Во–вторых, с ростом объём вычислений для этих методов слишком быстро возрастает и для n>10 они уже практически неприменимы. Для исследования систем линейных уравнений и нахождения их решений можно использовать метод Гаусса.

Исследовать систему – это значит определить совместна ли она и, в случае совместности, определить, сколько решений она имеет.

Определение. Расширенной матрицей С.Л.А.У. называется матрица, полученная из матрицы системы приписыванием справа столбца свободных членов системы.

Для системы из m уравнений с n неизвестными, она имеет размер m´(n+1) и обозначается через .

 

 

Свободные члены обычно отделяются вертикальной чертой.

Понятно, что ранг либо равен рангу A, либо превышает его на 1.

Следующая теорема позволяет устанавливать факт совместности или несовместности системы.

Теорема Кронекера – Капелли. Система линейных алгебраических уравнений совместна только в том случае, когда ранг её матрицы совпадает с рангом расширенной матрицы (r (A)= r ()).

Если r (A) r (), то СЛАУ решений не имеет.

Для совместных систем линейных уравнений верны следующие теоремы.

1. Если ранг матрицы совместной системы равен числу неизвестных, т.е. r=n, то система имеет единственное решение.

2. Если ранг матрицы совместной системы меньше числа неизвестных, т.е. r<n, то система неопределенная и имеет бесконечное множество решений.

Пусть r<n. r неизвестных называются базисными, если определитель матрицы из коэффициентов при них (т.е. базисный минор) отличен от нуля. Остальные n-r называются свободными.

При решении системы линейных уравнений не нужно отдельно вычислять ранги, а затем их сравнивать. Достаточно сразу применить метод Гаусса.

Преобразования Гаусса удобно проводить, осуществляя преобразования не над самими уравнениями, а над матрицей их коэффициентов.

Достоинства метода Гаусса по сравнению с другими:

· Значительно менее трудоемкий;

· Позволяет однозначно установить, совместна система или нет, а в случае совместности найти её решения (единственное или бесконечное множество);

· Дает возможность найти максимальное число линейно независимых уравнений – ранг матрицы системы.

Пример4.

Исследовать и решить систему

Запишем расширенную матрицу и приведём её к верхнетреугольному виду:

~ ~ ~

~ .

 

Мы получили, что r (A)=2, r ()=3 т.е. r (A) r (). Система решений не имеет.

Пример 5. Исследовать и решить систему

Запишем и приведем к верхнетреугольному виду матрицу .

~ ~ ~

~

т.к. r ()= r (A)=3 система совместна и имеет единственное решение. По последней матрице восстанавливаем систему и решаем её, начиная с последнего уравнения.

 

 

Пример 6. Исследовать и решить систему .

~ ~

 

~ ~ .

 

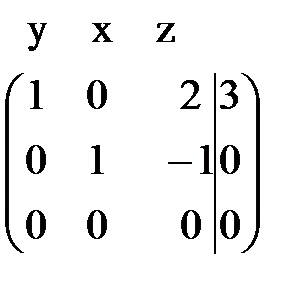Здесь r(A)= r()=2<3. Система имеет бесконечно много решений зависящих от 3–2=1 свободного неизвестного . Задавая свободному неизвестному произвольные значения =с, найдем бесконечное множество решений системы. Восстановим систему по последней матрице и решим её.

.